刷题记（入门DP） —— 2018.4.23

数塔，LCS，LIS，LCIS，01背包

前言

这次很多水题，因为是入门DP
DP这种东西，稍微变形我就不会了 QAQ

免费馅饼 - HDU 1176

题目大意
（略！）

思路
数塔模型
定义状态dp[i][j]：第i秒在j位置捡到的馅饼最大数量，则状态转移方程为
dp[i + 1][j + 1] = max(dp[i][j - 1] + a[i][j - 1], dp[i][j] + a[i][j], dp[i][j + 1] + a[i][j + 1])
然后倒过来走，因为最开始的位置是知道的

  #include <cstdio>
  #include <iostream>
  #include <cstring>
  #include <algorithm>
  using namespace std;
  const int N = 110000;

  int a[N][15];

  inline int mmax(int a, int b, int c){
      int p = a > b ? a : b;
      int q = b > c ? b : c;
      return p > q ? p : q;
  }

  int main(){
      int n;
      while(scanf("%d", &n) && n){
          memset(a[0], 0, sizeof(a));
          while(n--){
              int x, t;
              scanf("%d%d", &x, &t);
              a[t][x + 1]++;  //偏移一位，因为要dp的部分有j - 1，不偏移会越界
          }
          for(int i = N - 1; i >= 0; i--){
              for(int j = 1; j <= 11; j++){
                  a[i][j] += mmax(a[i + 1][j - 1], a[i + 1][j], a[i + 1][j + 1]);
              }
          }
          printf("%d\n", a[0][6]);
      }
  }

威威猫系列故事——打地鼠 - HDU 4540

题目大意
（继续略！）

思路
仍然是数塔模型
定义状态dp[i][j]为第i个时刻打位置为x的地鼠消耗的最小能量，则状态转移方程为
dp[i + 1][j] = min(|a[i + 1][j] - a[i][k]| + dp[i][k])

  #include <cstdio>
  #include <iostream>
  #include <cstring>
  using namespace std;
  const int N = 25;
  const int inf = 0x3f3f3f3f;

  inline int mabs(int a)        { return a < 0 ? -a : a; }
  inline int mmin(int a, int b) { return a < b ? a : b; }

  int dp[N][N], a[N][N];

  int main(){
      int n, m;
      while(~scanf("%d%d", &n, &m)){
          memset(dp[0], 0, sizeof(dp));
          for(int i = 0; i < n; i++){
              for(int j = 0; j < m; j++){
                  scanf("%d", &a[i][j]);
              }
          }
          for(int i = 0; i < n - 1; i++){
              for(int j = 0; j < m; j++){
                  int ans = inf;
                  for(int k = 0; k < m; k++){
                      ans = mmin(mabs(a[i + 1][j] - a[i][k]) + dp[i][k], ans);
                  }
                  dp[i + 1][j] = ans;
              }
          }

          int ans = inf;
          for(int j = 0; j < m; j++){
              ans = mmin(ans, dp[n - 1][j]);
          }
          printf("%d\n", ans);
      }
  }

Common Subsequence - HDU 1159

题目大意
求LCS

思路
LCS模板题

  #include <cstdio>
  #include <iostream>
  #include <vector>
  #include <algorithm>
  #include <cstring>
  using namespace std;
  const int N = 1e3 + 15;
  const int inf = 0x3f3f3f3f;

  char s[N], p[N];
  int dp[N][N];

  inline int mmax(const int& a, const int& b) { return a > b ? a : b; }

  int main()
  {
      while(~scanf("%s%s", s + 1, p + 1)){
          memset(dp[0], 0, sizeof(dp));
          int n = strlen(s + 1);
          int m = strlen(p + 1);
          for(int i = 1; i <= n; i++){
              for(int j = 1; j <= m; j++){
                  if(s[i] == p[j]){
                      dp[i][j] = dp[i - 1][j - 1] + 1;
                  }else{
                      dp[i][j] = mmax(dp[i - 1][j], dp[i][j - 1]);
                  }
              }
          }
          printf("%d\n", dp[n][m]);
      }
      return 0;
  }

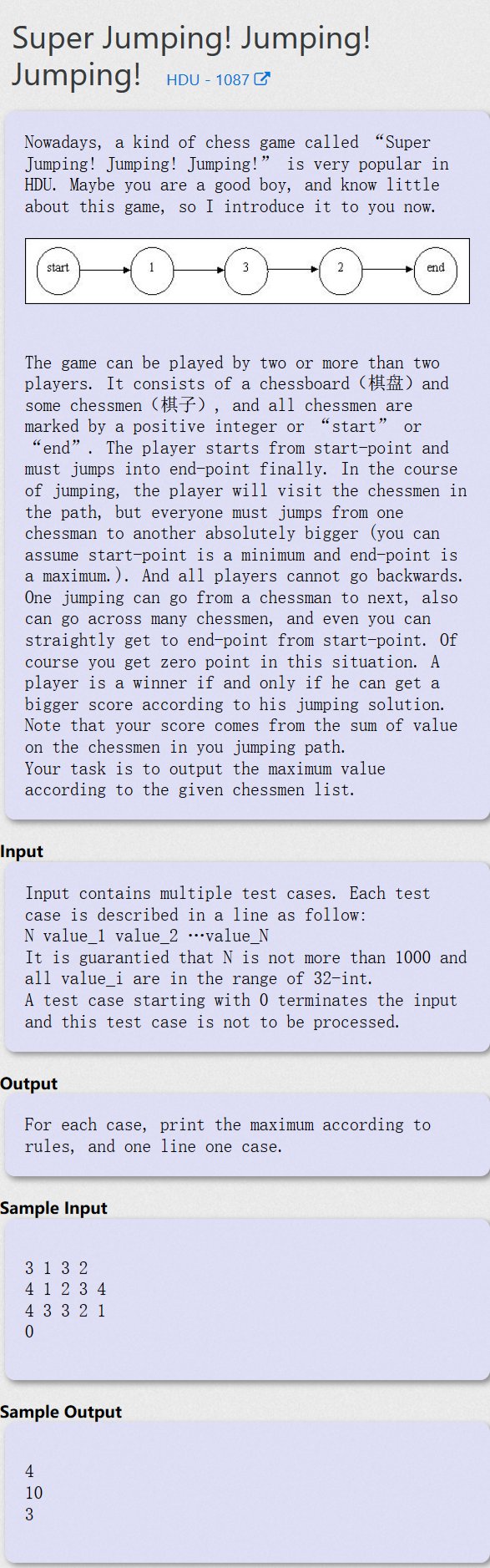
Super Jumping! Jumping! Jumping! - HDU-1087

题目大意
求严格递增子序列中和最大值

思路
LIS变形，原来LIS是DP长度的，现在DP和

  #include <iostream>
  #include <cstdio>
  #include <cstring>
  using namespace std;
  const int N = 1e3 + 15;
  const int inf = 0x3f3f3f3f;

  int dp[N], a[N];

  inline int mmax(int a, int b) { return a > b ? a : b; }

  int main()
  {
      int n;
      while(scanf("%d", &n) && n){
          memset(dp, 0, sizeof(dp));
          for(int i = 0; i < n; i++){
              scanf("%d", &a[i]);
          }
          dp[0] = a[0];
          for(int i = 1; i < n; i++){
              int ans = 0;
              for(int j = 0; j < i; j++){
                  if(a[j] < a[i]) ans = mmax(ans, dp[j]);
              }
              dp[i] = ans + a[i];
          }

          int ans = 0;
          for(int i = 0; i < n; i++){
              ans = mmax(ans, dp[i]);
          }
          printf("%d\n", ans);
      }
      return 0;
  }

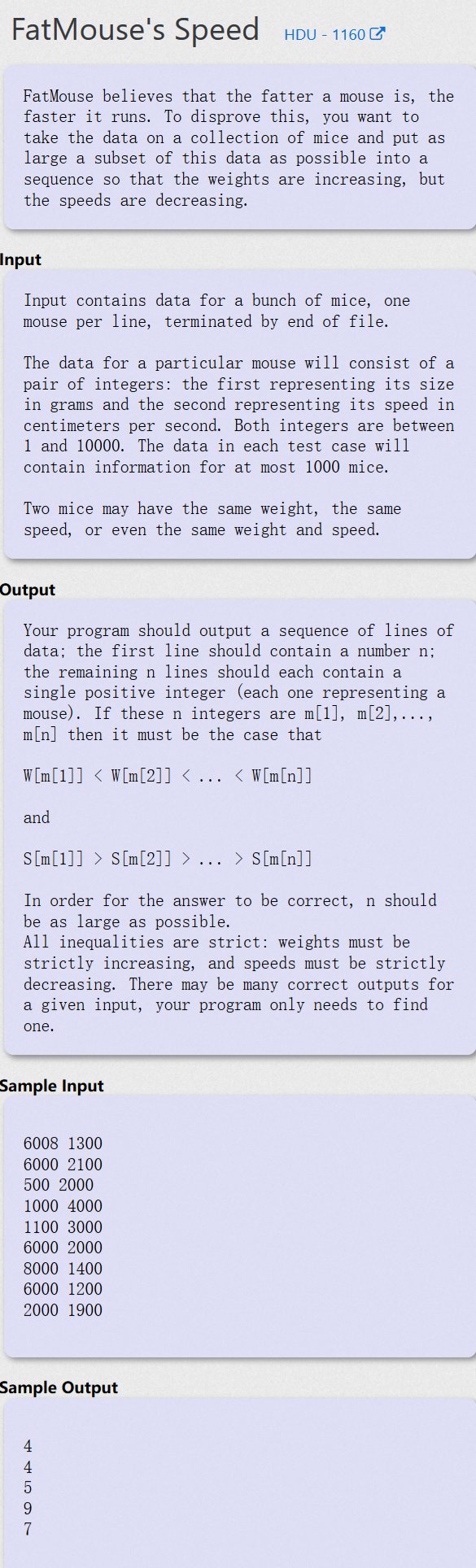
FatMouse’s Speed - HDU 1160

题目大意
给定n只老鼠的质量和速度，可重新排序求出一个序列，这个序列满足质量严格递减的情况下，速度严格递增，并且是所有满足上述条件下元素个数最多的

思路
LIS变形
按质量降序排序，然后用LIS求出满足条件的递增序列，并在此过程中用pre标记是接在哪个bj后面
最后搜索最大的dp，然后通过pre输出所有元素

  #include <cstdio>
  #include <iostream>
  #include <vector>
  #include <algorithm>
  #include <cstring>
  using namespace std;
  const int N = 1e3 + 15;
  const int inf = 0x3f3f3f3f;

  struct st{
      int m, v, p;
      bool operator <(const st& b){
          if(m != b.m)    return m > b.m;
          else            return v < b.v;
      }
  };
  st a[N];
  int dp[N];
  int pre[N];

  int main()
  {
      int tot = 0;
      memset(pre, -1, sizeof(pre));
      while(~scanf("%d%d", &a[tot].m, &a[tot].v)){
          a[tot].p = tot;
          tot++;
      }
      sort(a, a + tot);
      dp[0] = 1;
      for(int i = 1; i < tot; i++){
          int ansl = 0, ansp = -1;
          for(int j = 0; j < i; j++){
              if(a[j].v < a[i].v && a[j].m > a[i].m && ansl < dp[j]){
                  ansl = dp[j];
                  ansp = j;
              }
          }
          if(~ansp) { pre[i] = ansp; }
          dp[i] = ansl + 1;
      }

      int ans = 0, p = 0;
      for(int i = 0; i < tot; i++){
          if(ans < dp[i]){
              ans = dp[i];
              p = i;
          }
      }

      printf("%d\n", dp[p]);
      while(~p){
          printf("%d\n", a[p].p + 1);
          p = pre[p];
      }
      return 0;
  }

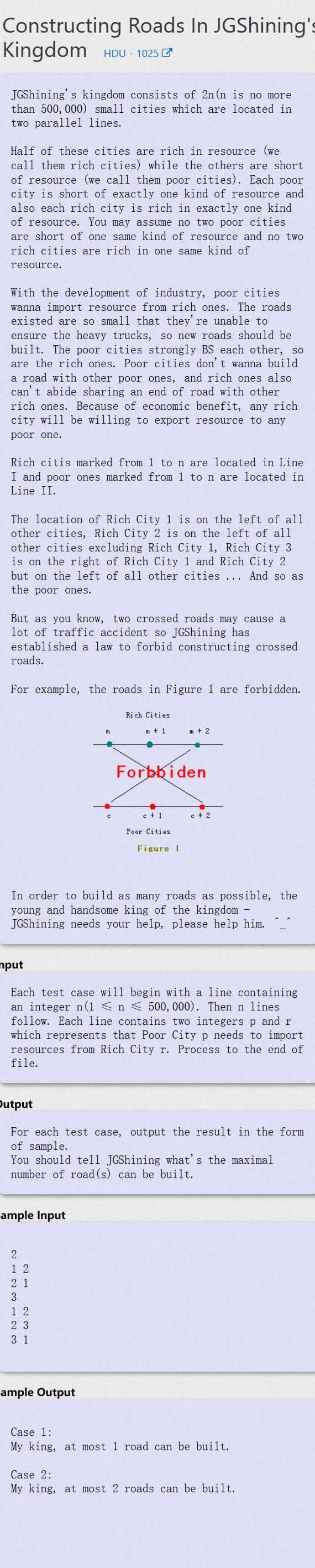
Constructing Roads In JGShining’s K - HDU-1025

题目大意
给定两条水平线上的2*n个点的连接情况，分别从左到右编号为1,2,…,n，求出最多数量的不相交线的集合的大小

思路
LIS变形
画图可以看出，可以把输入的两个点a b处理成road[a] = b，然后对road数组求LIS就是答案了

  #include <cstdio>
  #include <iostream>
  #include <algorithm>
  #include <cstring>
  using namespace std;
  const int N = 5e5 + 15;
  const int inf = 0x3f3f3f3f;

  int dp[N];
  int road[N];

  int main(){
      int n;
      int caseno = 1;
      while(~scanf("%d", &n)){
          memset(road, 0, sizeof(road));
          for(int i = 1; i <= n; i++){
              int a, b;
              scanf("%d%d", &a, &b);
              road[a] = b;
          }

          int mx = 0;
          for(int i = 1; i <= n; i++){
              int p = lower_bound(dp, dp + mx, road[i]) - dp;
              dp[p] = road[i];
              mx = max(mx, p + 1);
          }

          printf("Case %d:\n", caseno++);
          if(mx <= 1){
              printf("My king, at most %d road can be built.\n", mx);
          }else{
              printf("My king, at most %d roads can be built.\n", mx);
          }
          puts("");
      }
  }

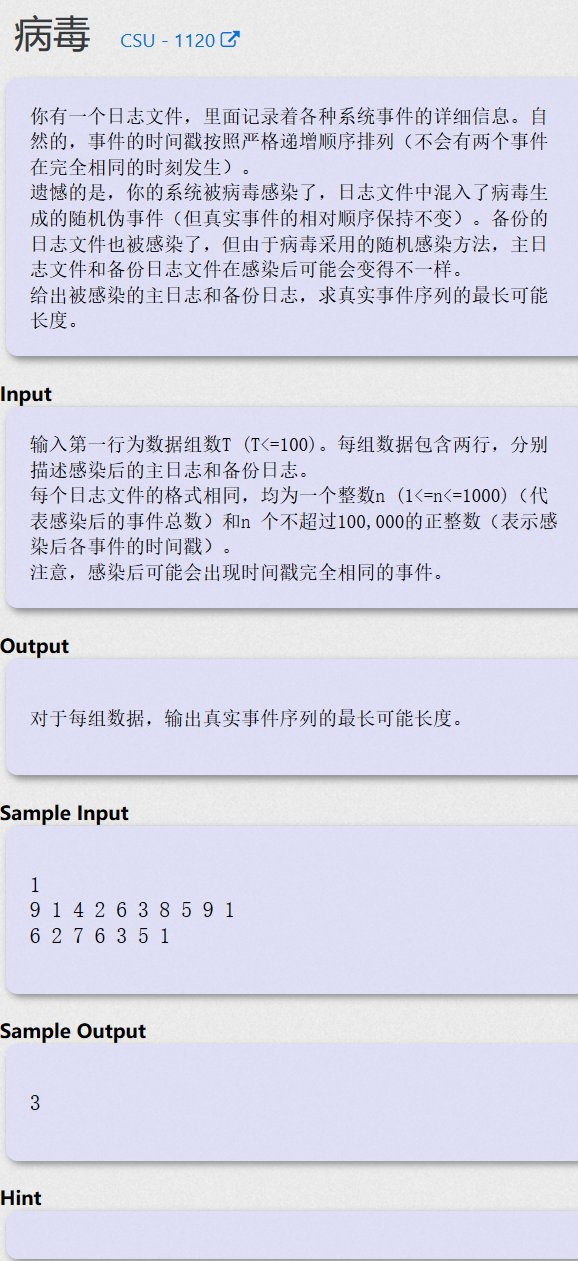
病毒 - CSU 1120

题目大意
(略略略！)

思路
LCIS模板题个人采用O(n*m)方法

  #include <cstdio>
  #include <iostream>
  #include <algorithm>
  #include <cstring>
  using namespace std;
  const int N = 1000 + 15;
  const int inf = 0x3f3f3f3f;

  int dp[2][N];
  int a[N], b[N];

  int main(){
      int t;
      scanf("%d", &t);
      while(t--){
          memset(dp[0], 0, sizeof(dp));
          int n, m;
          scanf("%d", &n);
          for(int i = 1; i <= n; i++){
              scanf("%d", &a[i]);
          }

          scanf("%d", &m);
          for(int i = 1; i <= m; i++){
              scanf("%d", &b[i]);
          }

          int ans = 0;
          for(int i = 1; i <= n; i++){
              int max_dp = 0;
              for(int j = 1; j <= m; j++){
                  dp[i&1][j] = dp[(i - 1)&1][j];
                  //此时a[i]是可能会存在b[j] == a[i]时的a[i]，所以把a[i]看作b[j]，b[j]看作b[k]，
                  //这样就和O(n^3)的解法中的状态转移方程相一致
                  if(a[i] > b[j]){    
                      max_dp = max(max_dp, dp[(i - 1)&1][j]);
                  }else if(a[i] == b[j]){
                      dp[i&1][j] = max_dp + 1;
                  }
                  ans = max(ans, dp[i&1][j]);
              }
          }

          printf("%d\n", ans);
      }
  }

Bone Collector - HDU 2602

题目大意
（虽然是英文但是依然略！）

思路
01背包模板题，因为之前写过了，所以这里只是回顾一下

  #include <cstdio>
  #include <iostream>
  #include <algorithm>
  #include <cstring>
  using namespace std;
  const int N = 1e3 + 15;
  const int inf = 0x3f3f3f3f;

  int w[N], c[N];
  int dp[N];

  int main(){
      int t;
      scanf("%d", &t);
      while(t--){
          memset(dp, 0, sizeof(dp));
          int n, lim;
          scanf("%d%d", &n, &lim);
          for(int i = 1; i <= n; i++)  scanf("%d", &c[i]);
          for(int i = 1; i <= n; i++)  scanf("%d", &w[i]);

          for(int i = 1; i <= n; i++){
              for(int j = lim; j - w[i] >= 0; j--){
                  dp[j] = max(dp[j - w[i]] + c[i], dp[j]);
              }
          }
          printf("%d\n", dp[lim]);
      }
  }