康托展开
前言
冒着生命危险码文……毕竟大物实验还没写完……
康托展开用来求一个数字在其全排列中排在第几位,可用做hash函数,而且这个hash函数niubility!因为可以求逆,和普通的hash函数不一样!
Eight - POJ 1077 && HDU 1043
 题目大意
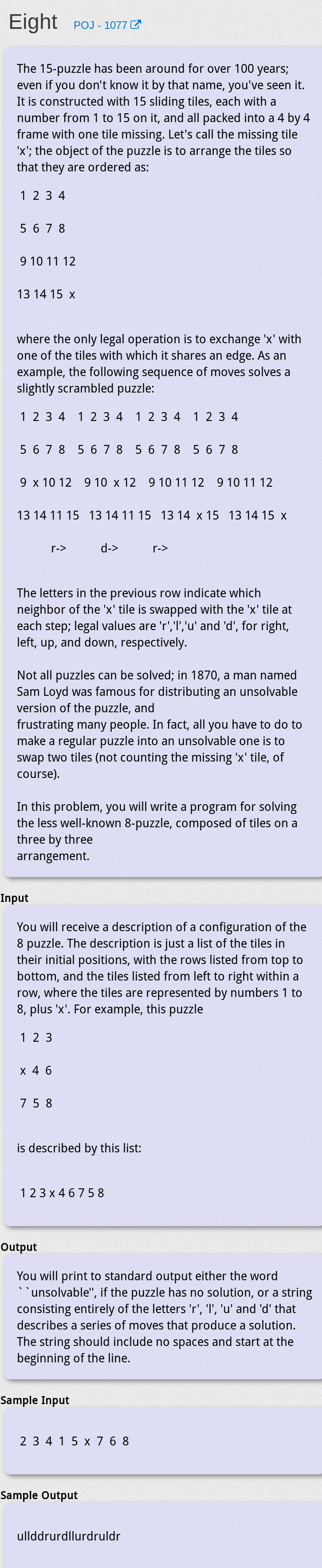
题目大意
八数码,以下来自 HIT 1868
在 3*3 的棋盘上有 8 个将牌,每一个将牌都刻有 1-8 数码中的某一个数码。棋盘中留有一个空格,允许其周围的某一个将牌向空格移动,这样通过移动将牌就可以不断改变将牌的布局。
给定一种初始时的将牌布局或结构(称作初始状态)和一个目标的布局(称作目标状态),问如何移动将牌,实现从初始状态到目标状态的改变,给出合法步骤
思路
本题其实是BFS,但是如何将整个数组作为状态压入队列呢?用康托展开压进去就可以了,取出来的时候再用康托展开的逆求出原数组
本题POJ和HDU是不一样的,POJ单组测试,HDU多组数据,所以能过POJ的代码不一定能过HDU
POJ中直接使用BFS,搜索过程中用pre标记是从哪个状态来的,输出的时候就递归输出就完事
HDU中因为是多组测试这样做会TLE,所以采用BFS打表,从最终状态开始BFS,直到队列为空,并用pre标记是到哪个状态去,输出的时候就直接从需求解的状态推到最终状态
POJ做法:
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cctype>
#include <queue>
#include <functional>
using namespace std;
typedef long long ll;
const int N = 9;
const int M = 4e5 + 15;
// 康托展开,从末位为第1位,首位为第n位
// X = a[n]*(n-1)! + a[n - 1]*(n-2)! + ... + a[1]*0!
struct node{
int x, prex, preop;
node(int px, int pprex, int ppop): x(px), prex(pprex), preop(ppop) {}
};
const int dx[] = {-1, 1, 0, 0};
const int dy[] = {0, 0, -1, 1};
const int fac[] = {1, 1, 2, 6, 24, 120, 720, 5040, 40320};
const char mp[] = "udlr";
queue<node> que;
bool used[M];
int pre[M]; //记录前一个结点(其实是图论)
int op[M]; //记录操作
inline void init(){
while(!que.empty()) que.pop();
memset(used, false, sizeof(used));
memset(pre, -1, sizeof(pre));
memset(op, -1, sizeof(op));
}
int cantor(int a[N]){
int sum = 0;
for(int i = 0; i < N; i++){
int cnt = 0;
for(int j = i + 1; j < N; j++){
if(a[j] < a[i]) cnt++; //后面的数比a[i]小的有几个
}
sum += cnt*fac[N - i - 1]; //sum += a[n] * (n - 1)!
}
return sum;
}
void inv_cantor(int num, int a[]){
bool used[N + 1] = {0};
for(int i = 0; i < N; i++){
int cnt = num/fac[N - i - 1]; //比a[i]小且未用过的数有cnt个
num %= fac[N - i - 1];
int j;
for(j = 0; j < N; j++){ //回推该位数字是几
if(!used[j]){
if(cnt == 0) break;
cnt--;
}
}
a[i] = j;
used[j] = true;
}
}
void display(int x){ //递归输出
if(pre[x] == -1) return;
display(pre[x]);
cout << mp[op[x]];
}
void bfs(int s, int t){
que.push(node(s, -1, -1));
while(!que.empty()){
node nd = que.front();
int x = nd.x;
que.pop();
if(used[x] == true) continue;
used[x] = true;
pre[x] = nd.prex;
op[x] = nd.preop;
if(x == t) break;
int a[N];
inv_cantor(x, a);
int xpos = 0;
while(a[xpos]) xpos++;
int i = xpos/3; //一维映射二维
int j = xpos%3;
for(int dir = 0; dir < 4; dir++){
int newi = i + dx[dir];
int newj = j + dy[dir];
if(newi < 0 || newi >= 3 || newj < 0 || newj >= 3) continue;
int newxpos = newi*3 + newj; //二维映射一维
swap(a[xpos], a[newxpos]);
int newx = cantor(a);
if(!used[newx]){
que.push(node(newx, x, dir));
}
swap(a[xpos], a[newxpos]);
}
}
}
int main(){
ios::sync_with_stdio(false);
while(true){
init();
int a[N];
int b[N] = {1,2,3,4,5,6,7,8,0};
char ch;
for(int i = 0; i < N; i++){
cin >> ch;
if(cin.eof()) break;
if('1' <= ch && ch <= '8') a[i] = ch - '0';
else a[i] = 0;
}
if(cin.eof()) break;
int s = cantor(a);
int t = cantor(b);
bfs(s, t);
if(s == t){
cout << "lr" << endl;
}else if(pre[t] == -1){
cout << "unsolvable" << endl;
}else{
display(t);
cout << endl;
}
}
}
HDU做法:
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cctype>
#include <queue>
#include <functional>
using namespace std;
typedef long long ll;
const int N = 9;
const int M = 4e5 + 15;
// 康托展开,从末位为第1位,首位为第n位
// X = a[n]*(n-1)! + a[n - 1]*(n-2)! + ... + a[1]*0!
struct node{
int x, prex, preop;
node(int px, int pprex, int ppop): x(px), prex(pprex), preop(ppop) {}
};
const int dx[] = {-1, 1, 0, 0};
const int dy[] = {0, 0, -1, 1};
const int fac[] = {1, 1, 2, 6, 24, 120, 720, 5040, 40320};
const char mp[] = "durl";
queue<node> que;
bool used[M];
int pre[M];
int op[M];
inline void init(){
while(!que.empty()) que.pop();
memset(used, false, sizeof(used));
memset(pre, -1, sizeof(pre));
memset(op, -1, sizeof(op));
}
int cantor(int a[N]){
int sum = 0;
for(int i = 0; i < N; i++){
int cnt = 0;
for(int j = i + 1; j < N; j++){
if(a[j] < a[i]) cnt++; //后面的数比a[i]小的有几个
}
sum += cnt*fac[N - i - 1];
}
return sum;
}
void inv_cantor(int num, int a[]){
bool used[N + 1] = {0};
for(int i = 0; i < N; i++){
int cnt = num/fac[N - i - 1];
num %= fac[N - i - 1];
int j;
for(j = 0; j < N; j++){
if(!used[j]){
if(cnt == 0) break;
cnt--;
}
}
a[i] = j;
used[j] = true;
}
}
void display(int x){
while(true){
if(x == -1) return;
cout << mp[op[x]];
x = pre[x];
}
}
void bfs(int s){
que.push(node(s, -1, -1));
while(!que.empty()){
node nd = que.front();
int x = nd.x;
que.pop();
if(used[x] == true) continue;
used[x] = true;
pre[x] = nd.prex;
op[x] = nd.preop;
int a[N];
inv_cantor(x, a);
int xpos = 0;
while(a[xpos]) xpos++;
int i = xpos/3;
int j = xpos%3;
for(int dir = 0; dir < 4; dir++){
int newi = i + dx[dir];
int newj = j + dy[dir];
if(newi < 0 || newi >= 3 || newj < 0 || newj >= 3) continue;
int newxpos = newi*3 + newj;
swap(a[xpos], a[newxpos]);
int newx = cantor(a);
if(!used[newx]){
que.push(node(newx, x, dir));
}
swap(a[xpos], a[newxpos]);
}
}
}
int main(){
ios::sync_with_stdio(false);
init();
int b[N] = {1,2,3,4,5,6,7,8,0};
int t = cantor(b);
bfs(t);
while(true){
int a[N];
char ch;
for(int i = 0; i < N; i++){
cin >> ch;
if(cin.eof()) break;
if('1' <= ch && ch <= '8') a[i] = ch - '0';
else a[i] = 0;
}
if(cin.eof()) break;
int s = cantor(a);
if(s == t){
cout << "lr" << endl;
}else if(pre[s] == -1){
cout << "unsolvable" << endl;
}else{
display(s);
cout << endl;
}
}
}
魔板 - HDU 1430
 题目大意
题目大意
(略)
思路
同样是康托展开,只是这题容易WA,QAQ
这题对于一开始的输入需要预处理,才能够始终对应BFS打的表,将初态映射为12345678,目态则一一对应映射
注意到题目要求字典序最小,所以搜索顺序就需要保持ABC(开优先队列反而WA了,后来想想用普通队列能够维持字典序最小,优先队列采用策略错误反而不能)
#include <iostream>
#include <cstdio>
#include <queue>
#include <cstring>
using namespace std;
const int N = 8;
const int M = 4e5 + 15;
const int fac[] = {1, 1, 2, 6, 24, 120, 720, 5040, 40320};
const char convert_op[] = "ABC";
struct node{
int val, op, pre;
node(int pval, int ppop, int ppre): val(pval), op(ppop), pre(ppre) {}
};
queue<node> que;
int op[M], pre[M];
bool used[M];
inline void init(){
while(!que.empty()) que.pop();
memset(op, -1, sizeof(op));
memset(pre, -1, sizeof(pre));
memset(used, false, sizeof(false));
}
int cantor(char a[]){
int sum = 0;
for(int i = 0; i < N; i++){
int cnt = 0;
for(int j = i + 1; j < N; j++){
if(a[j] < a[i]) cnt++;
}
sum += cnt*fac[N - i - 1];
}
return sum;
}
void inv_cantor(int num, char a[]){
bool used[N + 1] = {false};
for(int i = 0; i < N; i++){
int k = num/fac[N - i - 1];
num %= fac[N - i - 1];
int j;
for(j = 1; j <= N; j++){
if(!used[j]){
if(k == 0) break;
k--;
}
}
a[i] = j + '0';
used[j] = true;
}
}
void bfs(char s[]){
int sval = cantor(s);
que.push(node(sval, -1, -1));
while(!que.empty()){
node nd = que.front();
que.pop();
int val = nd.val;
if(used[val]) continue;
used[val] = true;
pre[val] = nd.pre;
op[val] = nd.op;
char a[N + 1] = {0};
inv_cantor(val, a);
//A:上下交换
for(int i = 0; i < 4; i++){ swap(a[i], a[N - i - 1]);}
int con_a_val = cantor(a);
if(!used[con_a_val]) que.push(node(con_a_val, 0, val));
for(int i = 0; i < 4; i++){ swap(a[i], a[N - i - 1]);}
//B:循环右移
for(int i = 2; i >= 0; i--) { swap(a[i], a[i + 1]);}
for(int i = 4; i <= N - 2; i++) { swap(a[i], a[i + 1]);}
int con_b_val = cantor(a);
if(!used[con_b_val]) que.push(node(con_b_val, 1, val));
for(int i = 0; i <= 2; i++) { swap(a[i], a[i + 1]);}
for(int i = N - 2; i >= 4; i--) { swap(a[i], a[i + 1]);}
//C:中心四格顺时针旋转
swap(a[5], a[6]);
swap(a[2], a[5]);
swap(a[1], a[2]);
int con_c_val = cantor(a);
if(!used[con_c_val]) que.push(node(con_c_val, 2, val));
}
}
void display(int val){
if(op[val] == -1) return;
display(pre[val]);
char a[10] = {0};
inv_cantor(val, a);
printf("%c", convert_op[op[val]]);
}
int main()
{
init();
char init_seq[] = "12345678";
bfs(init_seq);
char s[N + 1], t[N + 1];
while(~scanf("%s%s", s, t)){
//预处理完成映射
char mp[N + 1];
for(int i = 0; i < 8; i++){
mp[s[i] - '0'] = i + '0' + 1;
}
for(int i = 0; i < 8; i++){
t[i] = mp[t[i] - '0'];
}
int val = cantor(t);
display(val);
puts("");
}
}


