CodeForces Round #479(Div. 3)
前言
以后不打 Div.3 了,会打 Div.2 和 Div. 1,因为 Div.3 太简单了 (HouZAJ这只渣渣F题WA了6遍还在这里BB)
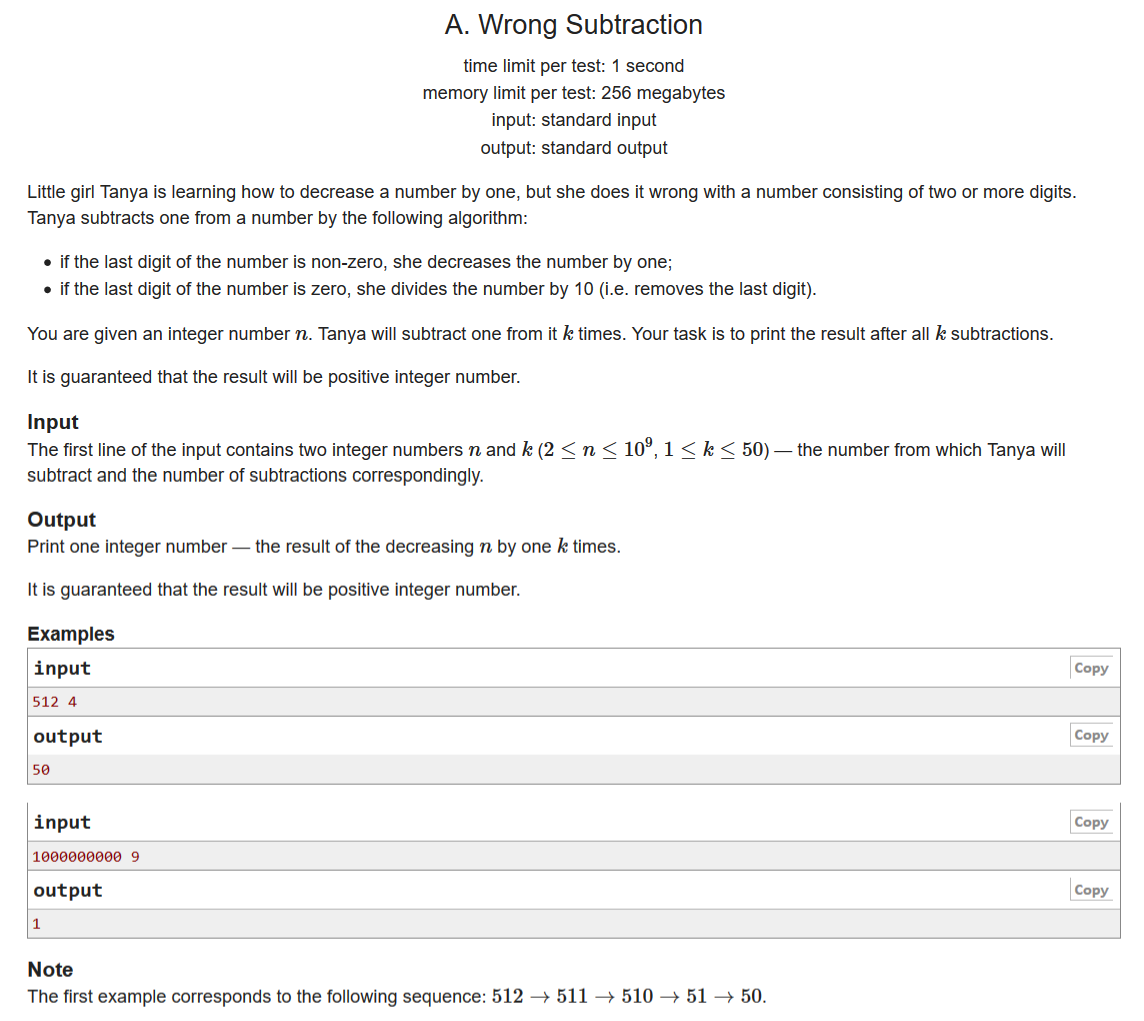
A. Wrong Subtraction
 题意
题意
给定整数n和k,k为操作次数,一次操作为:若n结尾非0则减1,若n结尾为0则把0删除,问最后的n是什么(题目数据保证最后的n是正数)
思路
大体上只是模拟,但是要加快模拟速度,对于结尾非0的,如果k还有剩余就直接求余,不足就慢慢减1,如果结尾是0的就除10,循环到k为0
#include <cstdio>
#include <iostream>
#include <cstring>
#include <queue>
#include <algorithm>
using namespace std;
const int N = 115;
const int inf = 0x3f3f3f3f;
int main(){
int n, k;
while(~scanf("%d%d", &n, &k)){
while(k){
if(n%10 == 0){
n /= 10;
k--;
}else{
if(k >= n%10){
k -= n%10;
n -= n%10;
}else{
n--;
k--;
}
}
}
printf("%d\n", n);
}
}
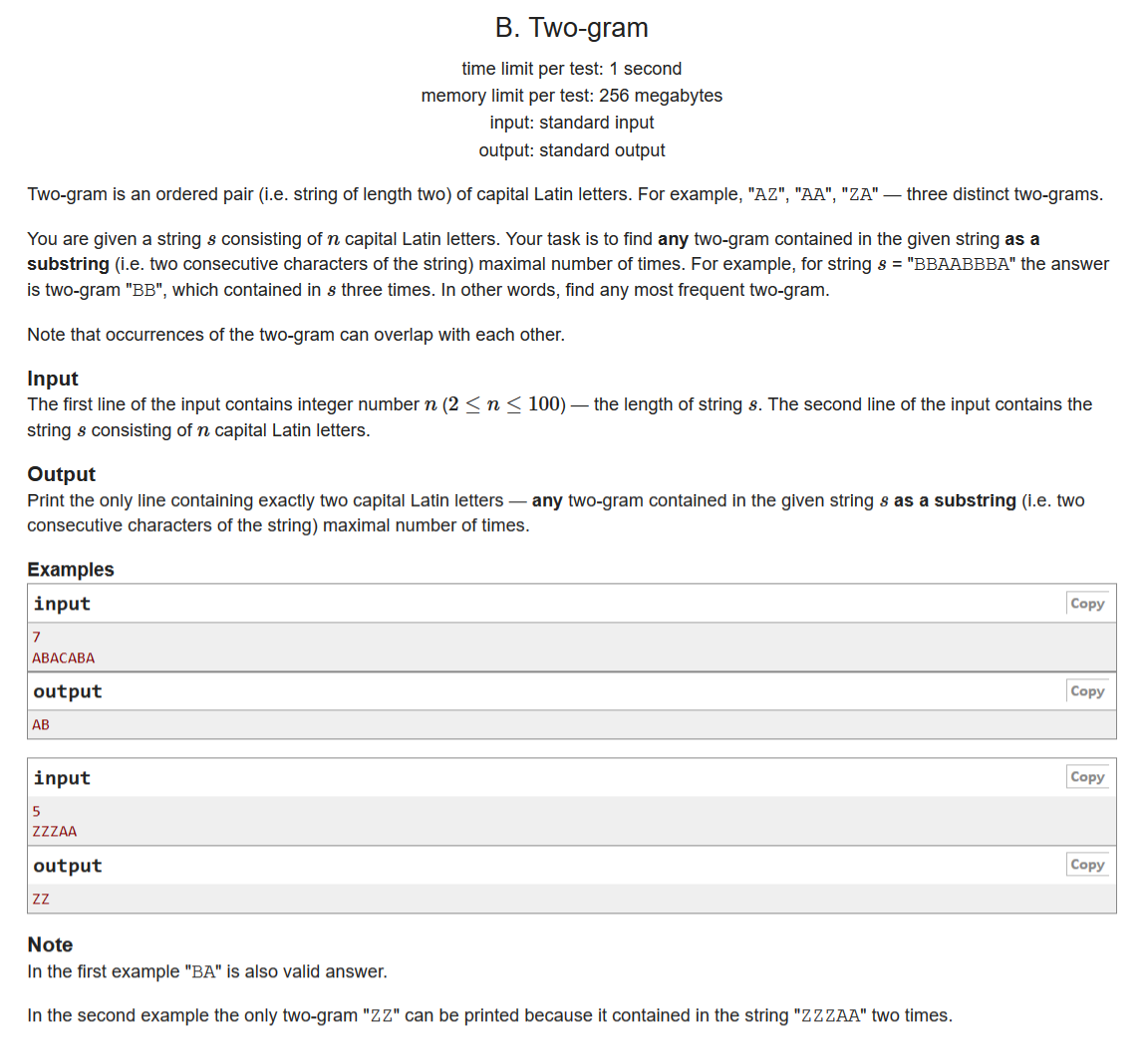
B. Two-gram
 题意
题意
求作为子串在给定字符串中出现次数最多的字母对(如AA,AB,BA之类的由两个字母组成的字符串)
思路
hash思想,把字母对当作数组下标存起来,每次扫到有这种字母对则对应位置的数组元素值++,最后扫一遍最大的出现的位置,把位置还原为字母对
#include <cstdio>
#include <iostream>
#include <cstring>
#include <queue>
#include <algorithm>
using namespace std;
const int N = 115;
const int inf = 0x3f3f3f3f;
char s[N];
int cnt[N*N];
int main(){
int n;
while(~scanf("%d%s", &n, s)){
memset(cnt, 0, sizeof(cnt));
for(int i = 0; i < n - 1; i++){
cnt[(s[i] - 'A') * 26 + (s[i + 1] - 'A')]++;
}
int ans = -1;
int pos = 0;
for(int i = 0; i < N*N; i++){
if(ans < cnt[i]){
ans = cnt[i];
pos = i;
}
}
char a = pos/26 + 'A';
char b = pos%26 + 'A';
printf("%c%c\n", a, b);
}
}
C. Less or Equal
 题意
题意
给定一个数组,求一个正整数x能满足有k个数小于或等于x,无解输出-1
思路
排序之后,直接看第k位和第k+1位是否相同,相同必定无解,同时如果给定的k=0,而数组中最小的元素又为1,那也是无解的,排除这两种情况后,当k!=0的时候,x可以直接等于第k位的元素,符合要求,当k=0的时候直接输出1
#include <cstdio>
#include <iostream>
#include <cstring>
#include <queue>
#include <algorithm>
using namespace std;
const int N = 115;
const int inf = 0x3f3f3f3f;
int a[N];
int main(){
int n, k;
while(~scanf("%d%d", &n, &k)){
for(int i = 0; i < n; i++) scanf("%d", &a[i]);
sort(a, a + n);
if(k == 0){
if(a[0] != 1) printf("1\n");
else printf("-1\n");
}else{
if(a[k - 1] == a[k]){
printf("-1\n");
}else{
printf("%d\n", a[k - 1]);
}
}
}
}
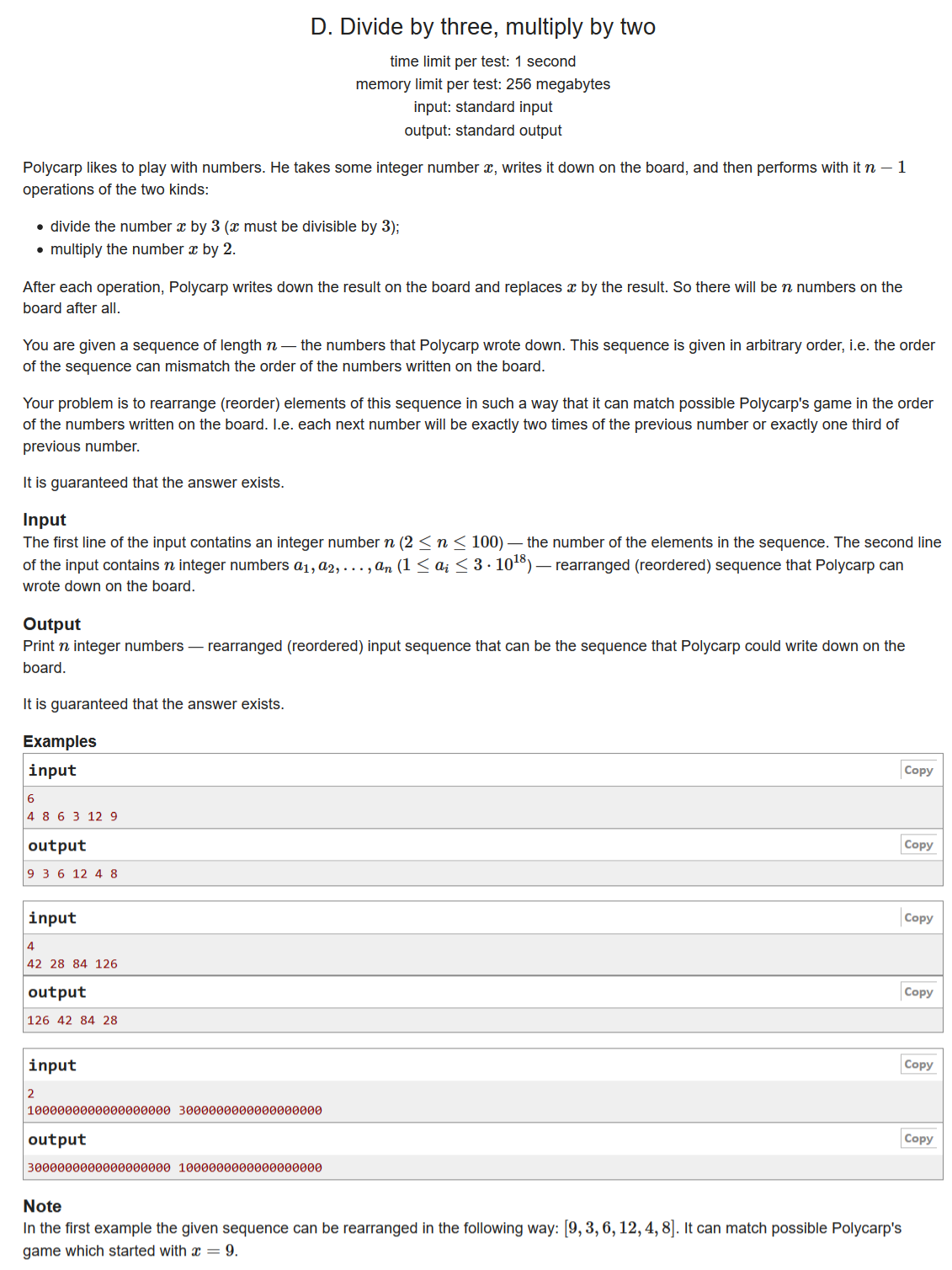
D. Divide by three, multiply by two
 题意
题意
给定数组,将数组元素重新排序,使得后一个元素是前一个元素/3或*2的结果
思路
因为数组最多100个元素,所以可以直接把答案搜出来,用set来标记元素是否在数组中,直到DFS的搜索深度能够达到数组元素个数,这时把答案保存下来即可。另外,每次搜/3和*2,最后答案还得倒过来,所以可以直接搜索为*3和/2,保存之后的答案无需倒置
#include <iostream>
#include <cstdio>
#include <set>
#include <vector>
using namespace std;
typedef long long ll;
set<ll> st;
vector<ll> vec;
void dfs(ll a, int dpt, int n, ll& ans){
if(dpt == n){
ans = a;
vec.push_back(a);
return;
}
if(ans == -1 && st.find(3*a) != st.end()){
dfs(3*a, dpt + 1, n, ans);
}
if(ans == -1 && a%2 == 0 && st.find(a/2) != st.end() && a%2 == 0){
dfs(a/2, dpt + 1, n, ans);
}
if(ans != -1){
vec.push_back(a);
}
}
int main(){
int n;
while(~scanf("%d", &n)){
vec.clear();
for(int i = 0; i < n; i++){
ll tmp;
scanf("%I64d", &tmp);
st.insert(tmp);
}
ll ans = -1;
for(set<ll>::iterator it = st.begin(); it != st.end() && ans == -1; it++){
dfs(*it, 1, n, ans);
}
for(int i = 0; i < vec.size(); i++){
printf("%I64d", vec[i]);
if(i < vec.size() - 1) putchar(' ');
}
puts("");
}
}
E. Cyclic Components
 题意
题意
给定一张图,求图中连通分量是单圈的个数
思路
其实可以想到,单圈中每个点的度数均为2,因此用并查集得出连通分量,然后再去判断连通分量中的每个点是否都是度数为2的点,最后扫一遍得到答案
#include <cstdio>
#include <cstring>
using namespace std;
const int N = 2e5 + 15;
struct edge{
int v, next;
};
bool tag[N];
int ft[N];
int idg[N];
int head[N];
int tot;
edge e[N << 1];
inline void init(int n){
memset(tag, true, sizeof(tag));
memset(head, -1, sizeof(head));
memset(idg, 0, sizeof(idg));
for(int i = 1; i <= n; i++) ft[i] = i;
tot = 0;
}
inline void addEdge(int u, int v){
e[tot].v = v;
e[tot].next = head[u];
head[u] = tot++;
idg[v]++;
}
int mfind(int x){ return x == ft[x] ? x : ft[x] = mfind(ft[x]); }
int main(){
int n, m;
while(~scanf("%d%d", &n, &m)){
init(n);
while(m--){
int u, v;
scanf("%d%d", &u, &v);
addEdge(u, v);
addEdge(v, u);
int p = mfind(u), q = mfind(v);
if(p != q){
ft[q] = p;
}
}
for(int i = 1; i <= n; i++){
if(idg[i] != 2){
tag[mfind(i)] = false;
}
}
int ans = 0;
for(int i = 1; i <= n; i++){
if(mfind(i) == i && tag[i]){
ans++;
}
}
printf("%d\n", ans);
}
return 0;
}
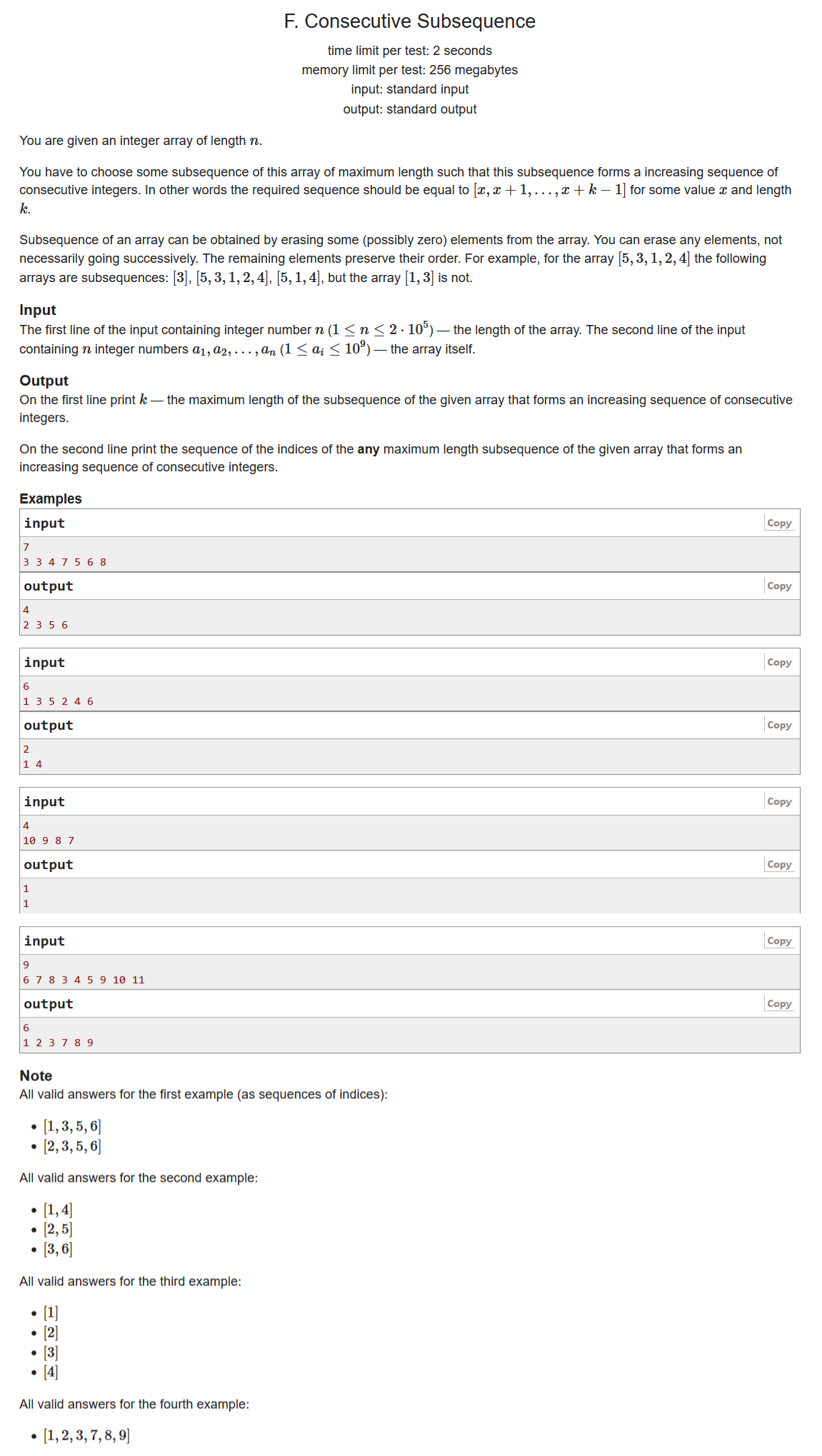
F. Consecutive Subsequence
 题意
题意
求最长连续递增子序列,输出下标
思路
实际上可以边读边dp,dp状态方程为 dp[x] = dp[x - 1] + 1,由于x太大,不能用数组保存为下标,所以使用map,dp过程中还有记录x对应在数组中的下标,以及记录前驱的位置,最终找到最大值及其对应下标,并递归输出即可
#include <cstdio>
#include <iostream>
#include <cstring>
#include <queue>
#include <algorithm>
#include <map>
using namespace std;
const int N = 2e5 + 15;
const int inf = 0x3f3f3f3f;
map<int, int> mp;
map<int, int> mp_pos;
int pre[N];
int res[N];
int tot;
void dfs(int x){
if(x == -1) return;
dfs(pre[x]);
res[tot++] = x;
}
int main(){
int n;
while(~scanf("%d", &n)){
mp.clear();
mp_pos.clear();
tot = 0;
int max_ans = 0, ans_pos;
for(int i = 1; i <= n; i++){
int tmp;
scanf("%d", &tmp);
mp_pos[tmp] = i;
if(mp.find(tmp - 1) == mp.end()){
mp[tmp] = 1;
pre[i] = -1;
}else{
mp[tmp] = mp[tmp - 1] + 1;
pre[i] = mp_pos[tmp - 1];
}
if(max_ans < mp[tmp]){
max_ans = mp[tmp];
ans_pos = i;
}
}
dfs(ans_pos);
printf("%d\n", max_ans);
for(int i = 0; i < tot; i++){
printf("%d", res[i]);
if(i < tot - 1) putchar(' ');
}
puts("");
}
}


