DFS, BFS, A*, 跳舞链
前言
没想到有HihoCoder这种网站是有教程的!
这次相关的解法看网站中的相关题目,懒得截图了 ^_^
搜索一·24点 - HihoCoder - 1304
 思路
思路
DFS求解24点
#include <cstdio>
#include <iostream>
#include <cstring>
#include <queue>
#include <vector>
#include <algorithm>
#include <cmath>
using namespace std;
const int N = 205;
const double inf = 1e8;
double a[4] = {0,0,0,0};
char ops[3] = {0,0,0};
char op_type[6] = {'+', '-',' * ','/','|','?'}; // | 是“反-”, ?是反“/”
double resCalc(double num1, double num2, char op){
if(op == '+') return num1 + num2;
else if(op == '-') return num1 - num2;
else if(op == '*') return num1 * num2;
else if(op == '/') return num1 / num2;
else if(op == '|') return num2 - num1;
else return num2 / num1;
}
// 计算在(((a ⊙ b) ⊙ c ) ⊙ d)形式下的值
bool calcType1(){
double res1 = resCalc(a[0], a[1], ops[0]);
double res2 = resCalc(res1, a[2], ops[1]);
double res3 = resCalc(res2, a[3], ops[2]);
return res3 == 24;
}
// 计算在((a ⊙ b) ⊙ (c ⊙ d))形式下的值
bool calcType2(){
double res1 = resCalc(a[0], a[1], ops[0]);
double res2 = resCalc(a[2], a[3], ops[2]);
double res3 = resCalc(res1, res2, ops[1]);
return res3 == 24;
}
bool dfsOps(int dpt){
if(dpt >= 3){
if(calcType1() || calcType2()) return true;
}else{
for(int i = 0; i < 6; i++){
ops[dpt] = op_type[i];
if(dfsOps(dpt + 1)) return true;
}
}
return false;
}
bool dfsNumber(){
sort(a, a + 4);
do{
if(dfsOps(0)) return true;
}while(next_permutation(a, a + 4));
return false;
}
int main(){
int t;
scanf("%d", &t);
while(t--){
for(int i = 0; i < 4; i++) scanf("%lf", &a[i]);
puts(dfsNumber() ? "Yes" : "No");
}
}
搜索二·骑士问题 - HihoCoder - 1308

思路
BFS问题
#include <cstdio>
#include <iostream>
#include <cstring>
#include <queue>
#include <algorithm>
#include <cmath>
using namespace std;
const int N = 205;
const int inf = 0x3f3f3f3f;
const int dx[] = {-2, -2, -1, -1, 1, 1, 2, 2};
const int dy[] = {-1, 1, -2, 2, 2, -2, -1, 1};
struct node{
int x, y, val;
node(int px, int py, int pv): x(px), y(py), val(pv) {}
};
int d[3][8][8];
bool used[8][8];
queue<node> que;
void bfs(int k, int sx, int sy){
memset(used, false, sizeof(used));
que.push(node(sx, sy, 0));
while(!que.empty()){
node u = que.front();
que.pop();
if(used[u.x][u.y]) continue;
used[u.x][u.y] = true;
d[k][u.x][u.y] = u.val;
for(int i = 0; i < 8; i++){
node v(u.x + dx[i], u.y + dy[i], u.val + 1);
if(v.x < 0 || v.x >= 8 || v.y < 0 || v.y >= 8 || used[v.x][v.y]) continue;
que.push(v);
}
}
}
int main(){
ios::sync_with_stdio(false);
int t;
cin >> t;
while(t--){
for(int k = 0; k < 3; k++){
char ch, num;
cin >> ch >> num;
int x = ch - 'A';
int y = num - '1';
bfs(k, x, y); //BFS求每一个棋子到任意位置的最少步数
}
int ans = inf;
for(int i = 0; i < 8; i++){ //求到同一位置的最少步数
for(int j = 0; j < 8; j++){
ans = min(ans, d[0][i][j] + d[1][i][j] + d[2][i][j]);
}
}
cout << ans << endl;
}
}
搜索三·启发式搜索 - HihoCoder - 1312
 思路
思路
A*算法
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cctype>
#include <queue>
#include <functional>
using namespace std;
typedef long long ll;
const int N = 9;
const int M = 4e5 + 15;
// 康托展开,从末位为第1位,首位为第n位
// X = a[n]*(n-1)! + a[n - 1]*(n-2)! + ... + a[1]*0!
struct node{
int x, as_val, val;
node(int px, int pasv, int pv): x(px), as_val(pasv), val(pv) {}
bool operator < (const node& b) const {
if(as_val != b.as_val) return as_val > b.as_val; //当前步数 + 曼哈顿距离作为首选
else return val > b.val; //当前步数作为次选
}
};
const int dx[] = {-1, 1, 0, 0};
const int dy[] = {0, 0, -1, 1};
const int fac[] = {1, 1, 2, 6, 24, 120, 720, 5040, 40320};
int target[N] = {1,2,3,4,5,6,7,8,0};
priority_queue<node> que;
bool used[M];
inline int mabs(int x){ return x < 0 ? -x : x; }
inline void init(){
while(!que.empty()) que.pop();
memset(used, false, sizeof(used));
}
int cantor(int a[N]){
int sum = 0;
for(int i = 0; i < N; i++){
int cnt = 0;
for(int j = i + 1; j < N; j++){
if(a[j] < a[i]) cnt++; //后面的数比a[i]小的有几个
}
sum += cnt*fac[N - i - 1];
}
return sum;
}
void inv_cantor(int num, int a[]){
bool used[N + 1] = {0};
for(int i = 0; i < N; i++){
int cnt = num/fac[N - i - 1];
num %= fac[N - i - 1];
int j;
for(j = 0; j < N; j++){
if(!used[j]){
if(cnt == 0) break;
cnt--;
}
}
a[i] = j;
used[j] = true;
}
}
int getH(int u){ //求曼哈顿距离,作为估价函数
int sum = 0;
int a[N];
inv_cantor(u, a);
for(int i = 0; i < 9; i++){
int num = (a[i] - 1 + 9)%9;
int sx = i/3, sy = i%3;
int tx = num/3, ty = num%3;
sum += (mabs(sx - tx) + mabs(sy - ty));
}
return sum;
}
int bfs(int s, int t){
que.push(node(s, getH(s), 0));
while(!que.empty()){
node nd = que.top();
int x = nd.x;
que.pop();
if(used[x] == true) continue;
used[x] = true;
if(x == t) return nd.val;
int a[N];
inv_cantor(x, a);
int xpos = 0;
while(a[xpos]) xpos++;
int i = xpos/3;
int j = xpos%3;
for(int dir = 0; dir < 4; dir++){
int newi = i + dx[dir];
int newj = j + dy[dir];
if(newi < 0 || newi >= 3 || newj < 0 || newj >= 3) continue;
int newxpos = newi*3 + newj;
swap(a[xpos], a[newxpos]);
int newx = cantor(a);
if(!used[newx]){
que.push(node(newx, nd.val + getH(newx) + 1, nd.val + 1));
}
swap(a[xpos], a[newxpos]);
}
}
return -1;
}
int main(){
int t;
scanf("%d", &t);
int e = cantor(target);
while(t--){
init();
int a[N];
for(int i = 0; i < N; i++){ scanf("%d", &a[i]); }
int s = cantor(a);
int ans = bfs(s, e);
if(ans == -1){
puts("No Solution!");
}else{
printf("%d\n", ans);
}
}
}
搜索四·跳舞链 - HihoCoder - 1317
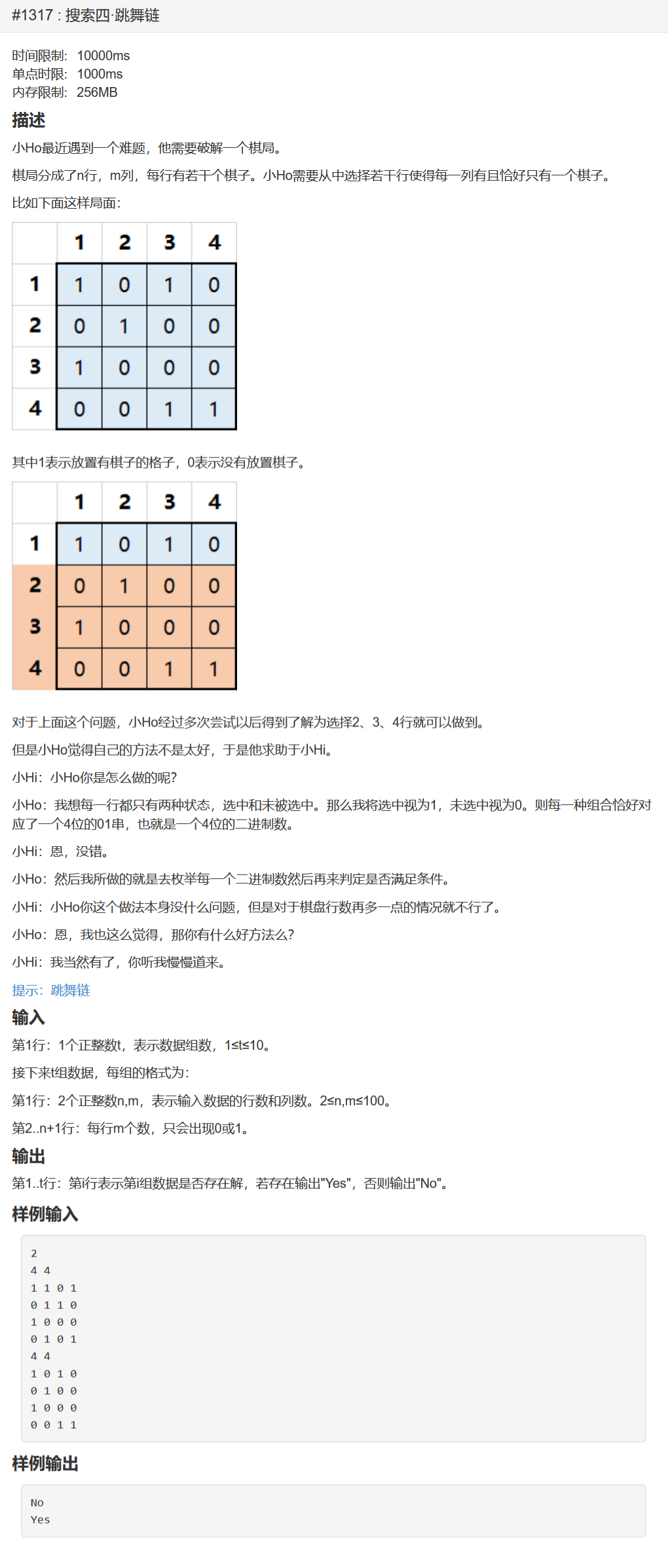 思路
思路
跳舞链基本问题
#include <cstdio>
#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;
const int N = 10005;
int tot;
int posx[N], posy[N]; //Node对应的posx和posy
int uu[N], dd[N], ll[N], rr[N]; //Node的上下左右指针
int row_id[N]; //每一行第一个Node的id
int col_cnt[N]; //每一列的Node个数
inline void init(int m){
tot = m + 1;
memset(row_id, -1, sizeof(row_id)); //初始化每一行第一个元素的id为-1
for(int i = 0; i <= m; i++){ //初始化列节点和Head节点,做好链接
col_cnt[i] = 0;
ll[i] = (i - 1 >= 0 ? i - 1 : m);
rr[i] = (i + 1 <= m ? i + 1 : 0);
uu[i] = dd[i] = i;
}
}
void link(int x, int y){
int id = tot;
posx[id] = x, posy[id] = y; //记录该节点位于哪一行哪一列
uu[id] = uu[y]; //做好链接
dd[id] = y;
uu[y] = id;
dd[uu[id]] = id;
if(row_id[x] == -1){
row_id[x] = ll[id] = rr[id] = id;
}else{
ll[id] = ll[row_id[x]];
rr[id] = row_id[x];
rr[ll[id]] = id;
ll[row_id[x]] = id;
}
col_cnt[y]++;
tot++;
}
void remove(int y){ //删除这一列(包括列节点),和列上有元素所在的行
ll[rr[y]] = ll[y]; //对于列节点,只需使其左右节点不指向它,自身左右不修改,便于恢复
rr[ll[y]] = rr[y];
for(int idj = dd[y]; idj != y; idj = dd[idj]){
for(int idi = rr[idj]; idi != idj; idi = rr[idi]){
uu[dd[idi]] = uu[idi]; //对于其中的节点,只需使其上下节点不指向它
dd[uu[idi]] = dd[idi]; //因为扫描是从列开始扫描的
col_cnt[posy[idi]]--;
}
}
}
void resume(int y){ //模拟递归时的恢复现场
for(int idj = uu[y]; idj != y; idj = uu[idj]){
for(int idi = ll[idj]; idi != idj; idi = ll[idi]){
uu[dd[idi]] = idi;
dd[uu[idi]] = idi;
col_cnt[posy[idi]]++;
}
}
ll[rr[y]] = y;
rr[ll[y]] = y;
}
bool dance(){
if(rr[0] == 0) return true;
int c = rr[0];
for(int id = rr[0]; id != 0; id = rr[id]){ //选择其中节点最少的列
if(col_cnt[id] < col_cnt[c]) c = id;
}
remove(c);
for(int idj = dd[c]; idj != c; idj = dd[idj]){
for(int idi = rr[idj]; idi != idj; idi = rr[idi]) remove(posy[idi]);
if(dance()) return true;
for(int idi = ll[idj]; idi != idj; idi = ll[idi]) resume(posy[idi]);
}
resume(c);
return false;
}
int main(){
int t;
scanf("%d", &t);
while(t--){
int n, m;
scanf("%d%d", &n, &m);
init(m);
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++){
int tmp;
scanf("%d", &tmp);
if(tmp){
link(i, j);
}
}
}
puts(dance() ? "Yes" : "No");
}
}
搜索五·数独 - HihoCoder - 1321
 思路
思路
跳舞链解数独
#include <cstdio>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <stack>
using namespace std;
const int N = 4e5 + 15;
int tot;
int posx[N], posy[N]; //Node对应的posx和posy
int uu[N], dd[N], ll[N], rr[N]; //Node的上下左右指针
int row_id[N]; //每一行第一个Node的id
int col_cnt[N]; //每一列的Node个数
int mat[800][400];
int G[10][10];
stack<int> stk;
void setMat(int i, int j, int k){
int id = (i - 1) * 9 + j; // 表示第i行第j列格子的编号
int pid = (id - 1) * 9 + k; // 表示该格子填写k所对应的方案编号
// 约束条件1 - 对应第1~81列
// 第(i-1) * 9+k列表示第i行存在数字k
mat[pid][(i - 1) * 9 + k] = 1;
// 约束条件2 - 对应第82~162列
// 第81+(j-1) * 9+k列表示第j列存在数字k
mat[pid][81 + (j - 1) * 9 + k] = 1;
// 约束条件3 - 对应第163~243列
// 第162+(t-1) * 9+k列表示第t个九宫存在数字k
int t = ((i - 1) / 3 * 3 + (j - 1) / 3) + 1;
mat[pid][162 + (t - 1) * 9 + k] = 1;
// 约束条件4 - 对应第244~324列
// 第243+id列表示第i行第j列填写有数字
mat[pid][243 + id] = 1;
}
inline void init(){
int m = 324;
while(!stk.empty()) stk.pop();
tot = m + 1;
memset(row_id, -1, sizeof(row_id)); //初始化每一行第一个元素的id为-1
for(int i = 0; i <= m; i++){ //初始化列节点和Head节点,做好链接
col_cnt[i] = 0;
ll[i] = (i - 1 >= 0 ? i - 1 : m);
rr[i] = (i + 1 <= m ? i + 1 : 0);
uu[i] = dd[i] = i;
}
}
void link(int x, int y){
int id = tot;
posx[id] = x, posy[id] = y; //记录该节点位于哪一行哪一列
uu[id] = uu[y]; //做好链接
dd[id] = y;
uu[y] = id;
dd[uu[id]] = id;
if(row_id[x] == -1){
row_id[x] = ll[id] = rr[id] = id;
}else{
ll[id] = ll[row_id[x]];
rr[id] = row_id[x];
rr[ll[id]] = id;
ll[row_id[x]] = id;
}
col_cnt[y]++;
tot++;
}
void createLinks(){
for(int i = 1; i < 800; i++){ //根据mat矩阵的结果链接节点
for(int j = 1; j < 400; j++){
if(mat[i][j]){
link(i, j);
}
}
}
}
void remove(int y){ //删除这一列(包括列节点),和列上有元素所在的行
ll[rr[y]] = ll[y]; //对于列节点,只需使其左右节点不指向它,自身左右不修改,便于恢复
rr[ll[y]] = rr[y];
for(int idj = dd[y]; idj != y; idj = dd[idj]){
for(int idi = rr[idj]; idi != idj; idi = rr[idi]){
uu[dd[idi]] = uu[idi]; //对于其中的节点,只需使其上下节点不指向它
dd[uu[idi]] = dd[idi]; //因为扫描是从列开始扫描的
col_cnt[posy[idi]]--;
}
}
}
void resume(int y){ //模拟递归时的恢复现场
for(int idj = uu[y]; idj != y; idj = uu[idj]){
for(int idi = ll[idj]; idi != idj; idi = ll[idi]){
uu[dd[idi]] = idi;
dd[uu[idi]] = idi;
col_cnt[posy[idi]]++;
}
}
ll[rr[y]] = y;
rr[ll[y]] = y;
}
bool dance(){
if(rr[0] == 0) return true;
int c = rr[0];
for(int id = rr[0]; id != 0; id = rr[id]){ //选择其中节点最少的列
if(col_cnt[id] < col_cnt[c]) c = id;
}
remove(c);
for(int idj = dd[c]; idj != c; idj = dd[idj]){
for(int idi = rr[idj]; idi != idj; idi = rr[idi]) remove(posy[idi]);
stk.push(posx[idj]);
if(dance()) return true;
for(int idi = ll[idj]; idi != idj; idi = ll[idi]) resume(posy[idi]);
stk.pop();
}
resume(c);
return false;
}
void solve(){
init();
createLinks();
dance();
while(!stk.empty()){
int x, y, k;
int pid = stk.top();
stk.pop();
for(int i = 1; i <= 81; i++){
if(mat[pid][i]){ //根据选择方案推算出第几行第几列填了几
x = (i - 1)/9 + 1;
k = i%9;
break;
}
}
for(int i = 82; i <= 162; i++){
if(mat[pid][i]){
y = (i - 82)/9 + 1;
break;
}
}
G[x][y] = (k ? k : 9);
}
for(int i = 1; i <= 9; i++){
for(int j = 1; j <= 9; j++){
printf("%d", G[i][j]);
if(j < 9) putchar(' ');
}
puts("");
}
}
int main(){
int t;
scanf("%d", &t);
while(t--){
memset(mat[0], 0, sizeof(mat));
for(int i = 1; i <= 9; i++){
for(int j = 1; j <= 9; j++){
scanf("%d", &G[i][j]);
if(G[i][j]){
setMat(i, j, G[i][j]);
}else{
for(int k = 1; k <= 9; k++){
setMat(i, j, k);
}
}
}
}
solve();
}
}


