带权并查集
前言
忽然发现自己怎么能把最后一道题的题意写的这么简单明了 [手动滑稽] 带权并查集,与普通的并查集相比,多了可推算集合内点关系的功能(因此难度也变大了)
- 带权并查集
https://blog.csdn.net/tribleave/article/details/72878239#%E5%B8%A6%E6%9D%83%E5%B9%B6%E6%9F%A5%E9%9B%86
https://agatelee.cn/2017/05/%E5%B8%A6%E6%9D%83%E5%B9%B6%E6%9F%A5%E9%9B%86/
Cube Stacking - POJ 1988
 题意
题意
有两种操作,第一种是M a b,把含有立方体a的堆叠在含有立方体b的堆上面,第二种是C a,询问立方体a下面有几个立方体。现在对于每个询问操作给出结果
思路
使用并查集维护当前堆的立方体总和sum_tot,和当前立方体下面立方体的数量sum_below,则
在合并操作中(这里将b堆在a上面)传导关系为sum_below[rb] = sum_tot[ra];,即b的根下面的立方体数量为sum_tot[a],sum_tot[ra] += sum_tot[rb];,即两堆合并
在路径压缩操作中传导关系为sum_below[x] += sum_below[xft];,即现在在x下方立方体的数量应为本来在x下方立方体的数量 + x原来的根下方立方体的数量(其在合并操作中已更新)
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 3e4 + 15;
int ft[N];
int sum_tot[N], sum_below[N];
inline void init(){
for(int i = 1; i < N; i++){
ft[i] = i;
sum_below[i] = 0;
sum_tot[i] = 1;
}
}
int find(int x){
if(ft[x] == x) return x;
int xft = ft[x];
ft[x] = find(ft[x]);
sum_below[x] += sum_below[xft];
return ft[x];
}
void merge(int a, int b){
int ra = find(a), rb = find(b);
if(ra != rb){
ft[rb] = ra;
sum_below[rb] = sum_tot[ra];
sum_tot[ra] += sum_tot[rb];
}
}
int main(){
int n;
char op[2];
while(~scanf("%d", &n)){
init();
while(n--){
scanf("%s", op);
if(op[0] == 'M'){
int a, b;
scanf("%d%d", &a, &b);
merge(b, a);
}else{
int x;
scanf("%d", &x);
find(x);
printf("%d\n", sum_below[x]);
}
}
}
}
Dragon Balls - HDU 3635
 题意
题意
每个城市(编号1到n)现在各有1颗龙珠(编号1到n),现在有两种操作
T a b: 将a城市的龙珠转移到b城市中
Q a:询问a龙珠所在的城市,a城市此时的龙珠数量,a龙珠的转移次数
思路
并查集应维护城市龙珠数量cnt_sum,和龙珠转移次数cnt_tran
a龙珠所在的城市即ft[a]
a城市此时的龙珠数量是并查集维护的cnt_sum
a龙珠的转移次数是并查集维护的cnt_tran
在路径压缩操作中,龙珠转移次数传导关系为cnt_tran[x] += cnt_tran[xft];,即当前该龙珠的转移次数为原来根的转移次数 + 该龙珠的转移次数,考虑到原来的根进行路径压缩后不再成为根,因此此这样写不会造成重复加
在合并操作中,城市龙珠数量传导关系为cnt_sum[ra] += cnt_sum[rb];,即合并,cnt_tran[rb]++;,即原来的根进行了本次转移,次数+1
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 1e4 + 15;
int cnt_sum[N], cnt_tran[N];
int ft[N];
inline void init(int n){
for(int i = 1; i <= n; i++){
ft[i] = i;
cnt_tran[i] = 0;
cnt_sum[i] = 1;
}
}
int find(int x){
if(ft[x] == x) return x;
int xft = ft[x];
ft[x] = find(ft[x]);
cnt_tran[x] += cnt_tran[xft];
return ft[x];
}
void merge(int a, int b){
int ra = find(a), rb = find(b);
if(ra != rb){
ft[rb] = ra;
cnt_sum[ra] += cnt_sum[rb];
cnt_tran[rb]++;
}
}
int main(){
int t, csn = 1;
scanf("%d", &t);
while(t--){
int n, q;
scanf("%d%d", &n, &q);
init(n);
char op[2];
int a, b;
printf("Case %d:\n", csn++);
while(q--){
scanf("%s", op);
if(op[0] == 'T'){
scanf("%d%d", &b, &a);
merge(a, b);
}else{
scanf("%d", &a);
find(a);
printf("%d %d %d\n", ft[a], cnt_sum[ft[a]], cnt_tran[a]);
}
}
}
return 0;
}
How Many Answers Are Wrong - HDU 3038
 题意
题意
给定一个序列的元素个数n以及信息个数q,对于每个信息,给出区间[a,b]中数的和,问信息中有多少条是矛盾的(若发生矛盾,则认为前面一条是正确的)
思路
几个月前看到这道题,一脸懵逼,现在好多了~
将区间个数和转化为 arr[a] + val = arr[b + 1],于是就变成了带权并查集区间合并的题目,用并查集维护节点到根节点的差值
路径压缩操作中,sum[x] += sum[xft];,即差值累加
合并操作中,若a与b同属于一个并查集,则计算差值,若与该信息矛盾,则这是一条矛盾的信息,否则进行合并操作sum[rb] = sum[a] + val - sum[b];,画图可得此传导关系
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 2e5 + 15;
int sum[N];
int ft[N];
inline void init(int n){
for(int i = 1; i <= n + 1; i++){
ft[i] = i;
sum[i] = 0;
}
}
int find(int x){
if(ft[x] == x) return x;
int xft = ft[x];
ft[x] = find(ft[x]);
sum[x] += sum[xft];
return ft[x];
}
int merge(int a, int b, int val){
int ra = find(a), rb = find(b);
if(ra == rb && val + sum[a] != sum[b]) return 0;
ft[rb] = ra;
sum[rb] = sum[a] + val - sum[b];
return 1;
}
int main(){
int n, q;
while(~scanf("%d%d", &n, &q)){
n++;
init(n);
int a, b, val;
int ans = 0;
while(q--){
scanf("%d%d%d", &a, &b, &val);
b++;
ans += !merge(b, a, val);
}
printf("%d\n", ans);
}
return 0;
}
分数调查 - HihoCoder 1515
 思路
思路
与上题是相同的,这里把差值算出来而已
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1e5 + 15;
int ft[N], rk[N];
inline void init(int n){
memset(rk, 0, sizeof(rk));
for(int i = 1; i <= n; i++) ft[i] = i;
}
int find(int x){
if(ft[x] == x) return x;
int xft = ft[x];
ft[x] = find(ft[x]);
rk[x] += rk[xft];
return ft[x];
}
void merge(int a, int b, int val){
int ra = find(a), rb = find(b);
if(ra != rb){
ft[rb] = ra;
rk[rb] = rk[a] + val - rk[b];
}
}
int main(){
int n, m, q;
while(~scanf("%d%d%d", &n, &m, &q)){
init(n);
while(m--){
int a, b, val;
scanf("%d%d%d", &a, &b, &val);
merge(a, b, val);
}
while(q--){
int a, b;
scanf("%d%d", &a, &b);
if(find(a) == find(b)){
printf("%d\n", rk[b] - rk[a]);
}else{
puts("-1");
}
}
}
}
Parity game - POJ 1733
 题意
题意
给定一个序列的长度n以及q个信息,每个信息给出区间[a,b]的和是奇数还是偶数,问第一条矛盾的信息的位置,若都不矛盾输出n
思路
首先题目给的范围太大,要么离散化处理,要么用map
使用并查集维护区间属性,1为奇数,0为偶数
则其传导可用异或实现,剩余内容不赘述
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <map>
using namespace std;
const int N = 2e5 + 15;
map<int, int> sum;
map<int, int> ft;
inline void init(){
sum.clear();
ft.clear();
}
int find(int x){
if(ft[x] == x) return x;
int xft = ft[x];
ft[x] = find(ft[x]);
sum[x] ^= sum[xft];
return ft[x];
}
int merge(int a, int b, int val){
int ra = find(a), rb = find(b);
if(ra == rb && (val ^ sum[a]) != sum[b]) return 0;
ft[rb] = ra;
sum[rb] = sum[a] ^ val ^ sum[b];
return 1;
}
int main(){
int n, q;
while(~scanf("%d%d", &n, &q)){
n++;
init();
int a, b, val;
char op[10];
int ans = 0;
bool flag = 0;
while(q--){
scanf("%d%d%s", &a, &b, op);
if(flag == 1) continue;
b++;
val = (op[0] == 'o');
if(ft.find(a) == ft.end()) ft.insert(pair<int, int>(a, a));
if(ft.find(b) == ft.end()) ft.insert(pair<int, int>(b, b));
if(!merge(b, a, val)) flag = 1;
else ans++;
}
printf("%d\n", ans);
}
return 0;
}
A Bug’s Life - POJ 2492
 题意
题意
有n只bug,给出q条信息,表示a、b两只bug的交♂配,问其中是否有gay
思路
用并查集维护当前节点与根节点的关系,0为同性,1为异性(注意不要颠倒,因为根节点与自身为同性)
由下两张图可得传导关系
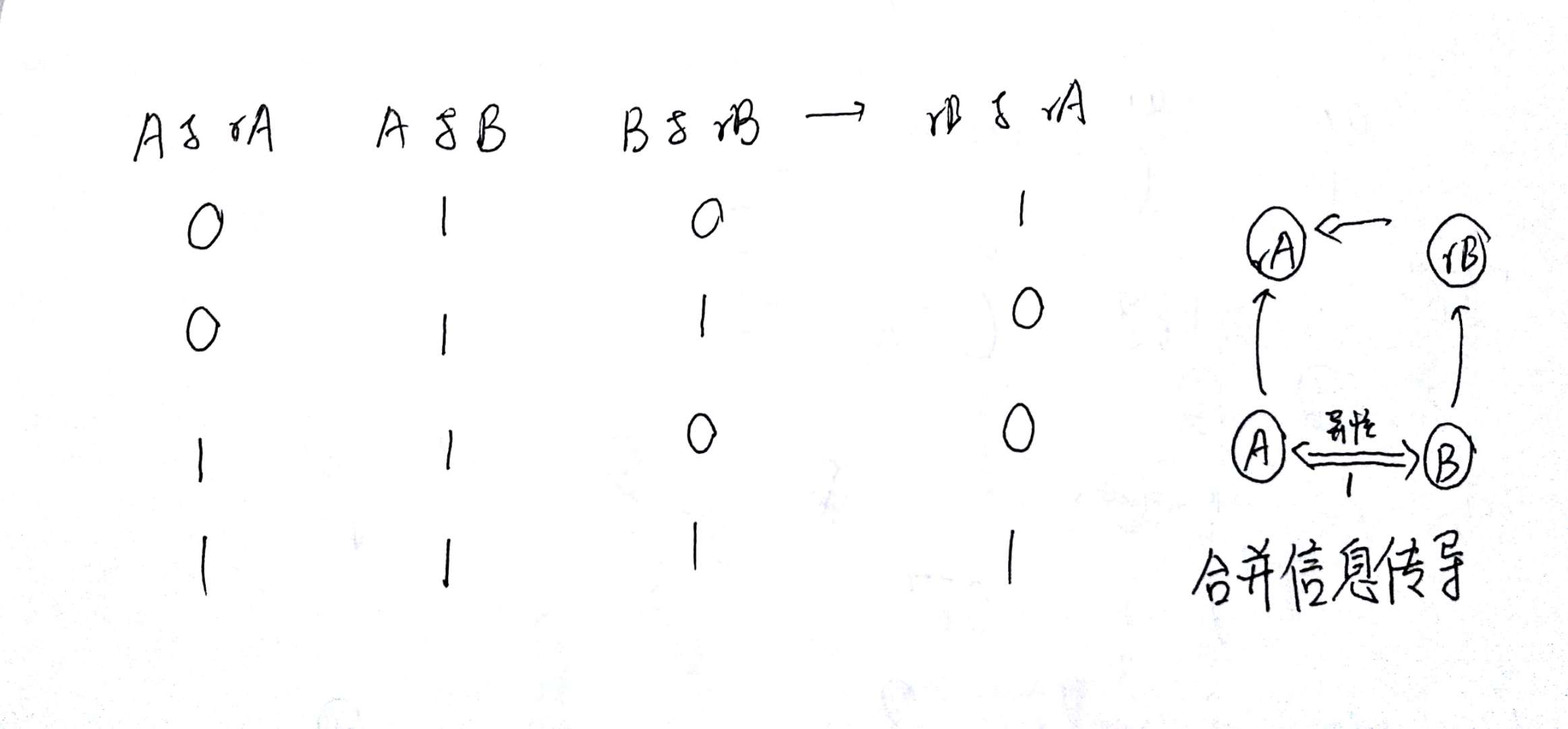
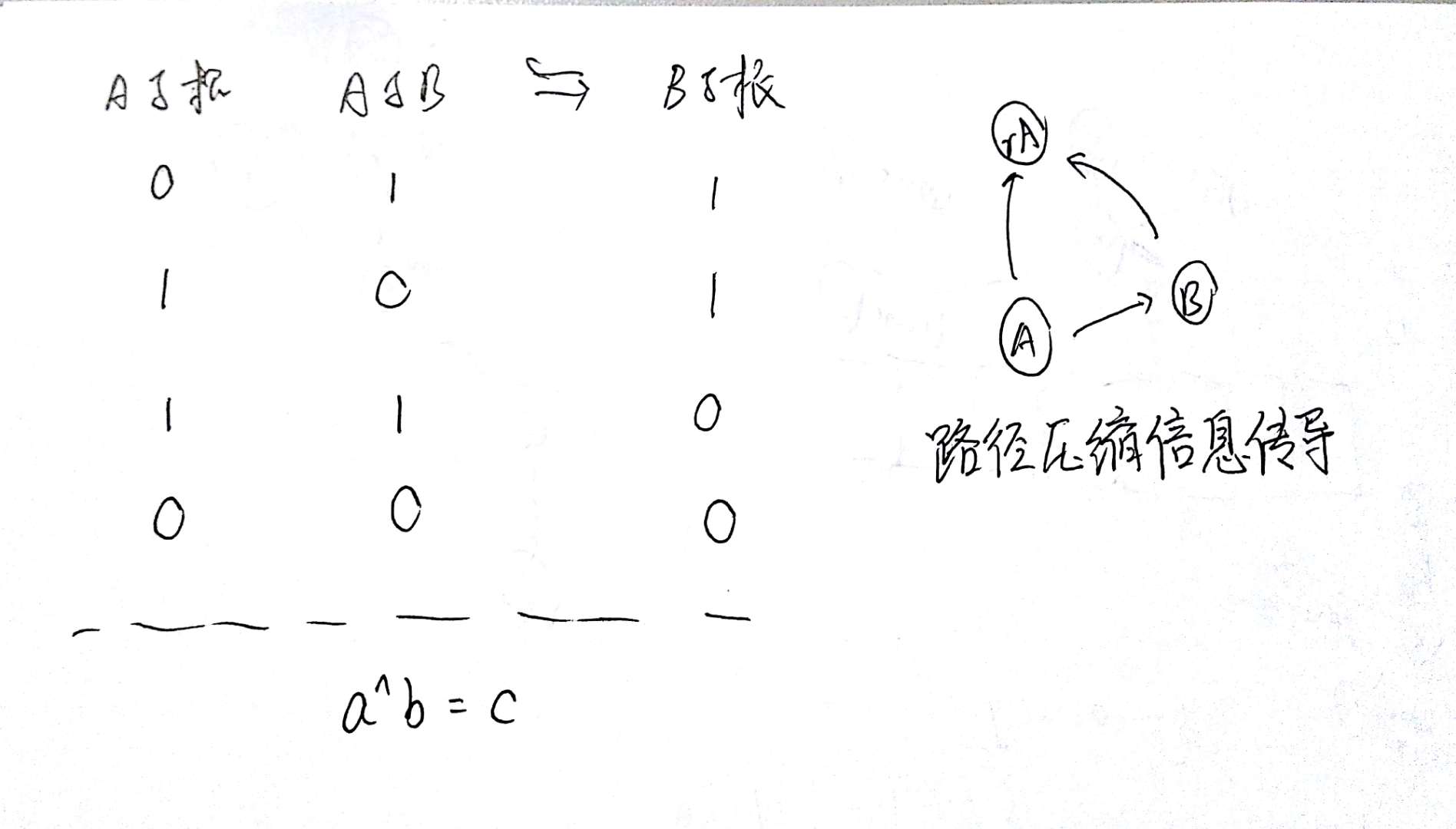
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <map>
using namespace std;
const int N = 1e6 + 15;
int ft[N];
int sex[N];
inline void init(int n){
for(int i = 1; i <= n; i++){
ft[i] = i;
sex[i] = 0;
}
}
int find(int x){
if(ft[x] == x) return x;
int xft = ft[x];
ft[x] = find(ft[x]);
sex[x] = sex[xft]^sex[x];
return ft[x];
}
int merge(int a, int b){
int ra = find(a), rb = find(b);
if(ra == rb && sex[a] == sex[b]) return 0;
ft[rb] = ra;
sex[rb] = sex[a]^1^sex[b];
return 1;
}
int main(){
int t, csn = 1;
scanf("%d", &t);
while(t--){
int n, q;
scanf("%d%d", &n, &q);
init(n);
int a, b;
int flag = 0;
while(q--){
scanf("%d%d", &a, &b);
if(!merge(a, b)) flag = 1;
}
if(csn > 1) puts("");
printf("Scenario #%d:\n", csn++);
puts(flag ? "Suspicious bugs found!" : "No suspicious bugs found!");
}
return 0;
}


