刷题记（博弈 I） —— 2018.7.15

巴什博弈、威佐夫博弈、Nim博弈、SG函数

前言

正在被博弈游戏玩 QAQ
PS：第一道JAVA打的题目献给威佐夫博弈 V2

kiki’s game - HDU 2147

题意
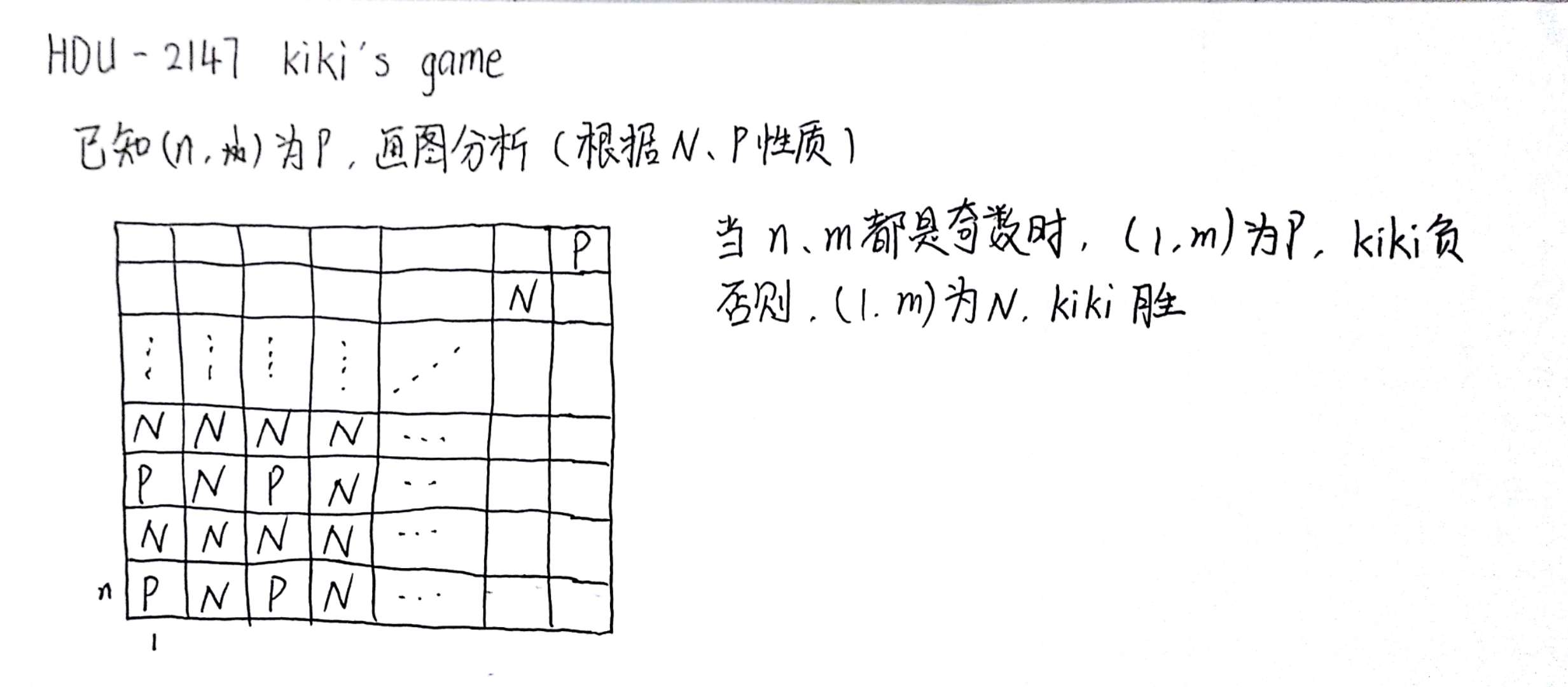
给定一个n*m的棋盘，在(1,m)处有一颗棋子，双方轮流玩，每一次玩家都可以将棋子往左边移动一格，或者往下边移动一格，或者往左下方移动一格，直到不能移动为止，问谁会赢？
思路
见下图

  #include <cstdio>
  using namespace std;

  int main(){
      int n, m;
      while (~scanf("%d%d", &n, &m) && n + m) {
          puts(n&m&1 ? "What a pity!" : "Wonderful!");
      }
  }

A Multiplication Game - HDU 1517

题意
给定一个数n，双方轮流玩游戏，从p=1开始，双方都可以选择2-9内的任意数乘上p再赋值给p，第一个使得p>=n的人赢，问谁会赢
思路
见下图

  #include <cstdio>
  #include <algorithm>
  #include <cstring>
  using namespace std;
  const int N = 1e5 + 15;

  int main(){
      unsigned n;
      while(~scanf("%u", &n)){
          int i = 0;
          while(n > 1){
              if(i)   n = (n + 1)/2;
              else    n = (n + 8)/9;
              i ^= 1;
          }
          puts(i ? "Stan wins." : "Ollie wins.");
      }
  }

威佐夫游戏 - 51Nod 1072

思路
模板题

  #include <bits/stdc++.h>
  using namespace std;

  int main(){
      int t;
      scanf("%d", &t);
      while(t--){
          int a, b, minn;
          scanf("%d%d", &a, &b);
          minn = min(a, b);
          long k = (int)fabs(b - a) * (sqrt(5) + 1)/2;
          printf("%c\n", k != minn ? 'A' : 'B');
      }
      return 0;
  }

威佐夫游戏 V2 - 51Nod 1185

思路
需高精度，故用JAVA 至于那个(sqrt(5) + 1)/2的结果是怎么来的，当然是用计算器算出来的

  import java.math.BigDecimal;
  import java.util.Scanner;

  public class Main{
      public static void main(String args[]){
          Scanner cin = new Scanner(System.in);
          int t = cin.nextInt();
          while(t > 0){
              t--;

              long a = cin.nextLong(), b = cin.nextLong();
              long minn = Math.min(a, b);
              BigDecimal dis = new BigDecimal(String.valueOf(Math.abs(b - a)));
              //(sqrt(5)+1)/2
              BigDecimal k   = new BigDecimal("1.6180339887498948482045868343656381177200");    
              BigDecimal tmp = k.multiply(dis);
              long ans = tmp.longValue();
              System.out.println(ans == minn ? 'B' : 'A');
          }
      }
  }

Being a Good Boy in Spring Festival - HDU 1850

思路
Nim博弈
第一步有几种方案就是在第一步时把P态推给对方，设异或和为xorsum，即是要把xorsum变为0,而根据游戏规则，只允许数变小，不允许数变大，所以就要判定a[i] > xorsum^a[i]是否成立，成立就说明可以把a[i]变为xorsum^a[i]，使得xorsum变为0，逐个枚举统计结果即可

  #include <cstdio>
  using namespace std;
  const int N = 100;

  int a[N];

  int main()
  {
      int n;
      while(~scanf("%d", &n) && n){
      	int xorsum = 0;
      	int ans = 0;
      	for(int i = 0; i < n; i++){
      		scanf("%d", &a[i]);
      		xorsum ^= a[i];
      	}
      	for(int i = 0; i < n; i++){
      		if(a[i] > (xorsum^a[i]))  ans++;
      	}
      	printf("%d\n", ans);
      }
      return 0;
  }

Northcott Game - HDU 1730

思路
其实题目等价于：给定n个卡牌堆，双方可以任选一堆改变卡牌堆的数量（最小为1），最后能使得每堆都只剩下1张卡牌的一方获胜
那么这与Nim博弈非常类似，实际上只要把每堆减去1,再规定只允许减少不允许增加就是Nim博弈了，而允许增加并不会改变异或和为0会P态的结论，只需要在异或时将每堆的数量减去1再异或就是Nim博弈

  #include <cstdio>
  #include <algorithm>
  #include <cstring>
  using namespace std;
  const int N = 1e2;

  inline int mabs(int x){ return x > 0 ? x : -x; }

  int main(){
      int n, m;
      while(~scanf("%d%d", &n, &m)){
          int a, b, xorsum = 0;
          while(n--){
              scanf("%d%d", &a, &b);
              xorsum ^= (mabs(a - b) - 1);
          }
          puts(xorsum == 0 ? "BAD LUCK!" : "I WIN!");
      }
  }

S-Nim - HDU 1536

题意
懒得翻译
思路
构造SG函数模板题

  #include <cstdio>
  #include <algorithm>
  #include <cstring>
  using namespace std;
  const int N = 1e4 + 15;

  int SG[N], s[N];
  bool used[N];

  void getSG(int n){
      SG[0] = 0;
      //排序为取最小值，以及更快的结束下面的循环
      sort(s + 1, s + n + 1);

      for(int i = s[0]; i < N; i++){
          memset(used, false, sizeof(used));
          for(int j = 1; j <= n; j++){
              if(i - s[j] < 0)    break;
              //标记此SG值出现过
              used[SG[i - s[j]]] = true;  
          }

          //从0开始找第一个没有出现的SG值（mex操作）
          for(int j = 0; j < N; j++){
              if(!used[j]){
                  SG[i] = j;
                  break;
              }
          }
      }
  }

  int main(){
      int n, m;
      while(~scanf("%d", &n) && n){
          for(int i = 1; i <= n; i++)     scanf("%d", &s[i]);
          getSG(n);

          scanf("%d", &m);
          while(m--){
              int xorsum = 0;
              int k;
              scanf("%d", &k);
              while(k--){
                  int tmp;
                  scanf("%d", &tmp);
                  xorsum ^= SG[tmp];
              }
              putchar(xorsum ? 'W' : 'L');
          }
          puts("");
      }
  }

A New Tetris Game - HDU 1760

思路
用DFS判断一开始是否为N态
要使一开始为N态，只需要在DFS下一层时存在P态即可，而要使某一层为P态，需要在它下一层不存在P态

  #include <cstdio>
  #include <algorithm>
  #include <cstring>
  using namespace std;
  const int N = 50 + 15;

  char G[N][N];

  bool dfs(int n, int m){
      for(int i = 0; i < n - 1; i++){
          for(int j = 0; j < m - 1; j++){
              if(G[i][j] == '0' && G[i + 1][j] == '0' && G[i][j + 1] == '0' && G[i + 1][j + 1] == '0'){
                  G[i][j] = G[i + 1][j] = G[i][j + 1] = G[i + 1][j + 1] = '1';
                  if(!dfs(n, m)){
                      G[i][j] = G[i + 1][j] = G[i][j + 1] = G[i + 1][j + 1] = '0';
                      return true;
                  }
                  G[i][j] = G[i + 1][j] = G[i][j + 1] = G[i + 1][j + 1] = '0';
              }
          }
      }
      return false;
  }

  int main(){
      int n, m;
      while(~scanf("%d%d", &n, &m)){
          for(int i = 0; i < n; i++){
              getchar();
              for(int j = 0; j < m; j++){
                  G[i][j] = getchar();
              }
          }
          puts(dfs(n, m) ? "Yes" : "No");
      }
  }

A New Tetris Game(2) - HDU 1809

思路
与上题相比，需要构造SG函数
另外，需要记忆化搜索

  #include <cstdio>
  #include <algorithm>
  #include <cstring>
  #include <map>
  using namespace std;
  const int N = 55;

  char G[N][N];

  map<string, int> mpG;

  string tos(int n){
      string s;
      for(int i = 0; i < n; i++){
          s += G[i];
          s += ' * ';   //为防止两个非同型矩阵转一维后得到相同的结果
      }
      return s;
  }

  int dfs(int n, int m){
      bool used[N << 1];
      memset(used, 0, sizeof(used));
      string s = tos(n);
      if(mpG.find(s) != mpG.end())  return mpG[s];

      for(int i = 0; i < n - 1; i++){
          for(int j = 0; j < m - 1; j++){
              if(G[i][j] == '0' && G[i + 1][j] == '0' && G[i][j + 1] == '0' && G[i + 1][j + 1] == '0'){
                  G[i][j] = G[i + 1][j] = G[i][j + 1] = G[i + 1][j + 1] = '1';
                  used[dfs(n, m)] = 1;
                  G[i][j] = G[i + 1][j] = G[i][j + 1] = G[i + 1][j + 1] = '0';
              }
          }
      }
      for(int i = 0; ; i++){
          if(!used[i]){
              mpG[s] = i;
              return i;
          }
      }
  }

  int main(){
      int t;
      while(~scanf("%d", &t)){
          int xorsum = 0;
          while(t--){
              int n, m;
              scanf("%d%d", &n, &m);
              for(int i = 0; i < n; i++){
                  scanf("%s", G[i]);
              }
              xorsum ^= dfs(n, m);
          }
          puts(xorsum ? "Yes" : "No");
      }
  }