树形DP I
前言
本次内容比较水,算是接触树形DP吧,谈不上入门
- 树形DP
https://blog.csdn.net/txl199106/article/details/45373507
https://www.cnblogs.com/mhpp/p/6628548.html
Anniversary party - HDU - 1520

题意
给定一棵树,子节点和父亲节点不能同时选,问最大价值
思路
定义DP状态f[u][0]为不选u节点的最大价值,f[u][1]为选了u节点的最大价值,则对于u的孩子节点v
f[u][0] = sum(max(f[v][0], f[v][1])),不选了u,v也可以选也可以不选
f[u][1] = sum(f[v][0])选了u,v只能不选
DFS从上往下扫一遍,在回溯时DP即可
#include <cstdio>
#include <cstring>
#include <cmath>
#include <ctime>
#include <algorithm>
#include <functional>
using namespace std;
typedef long long ll;
const int N = 6000 + 15;
const int inf = 0x3f3f3f3f;
struct edge{
int v, nxt;
};
edge e[N];
int head[N], tot;
int used[N];
int f[N][2];
inline void init(){
memset(f, 0, sizeof(f));
memset(head, -1, sizeof(head));
tot = 0;
}
inline void addEdge(int u, int v){
e[tot] = edge{v, head[u]};
head[u] = tot++;
used[v] = true;
}
void dfs(int u){
used[u] = true;
for(int i = head[u]; ~i; i = e[i].nxt){
int v = e[i].v;
if(!used[v]) dfs(v);
f[u][0] += max(f[v][0], f[v][1]);
f[u][1] += f[v][0];
}
}
int main(){
int n;
while(~scanf("%d", &n)){
init();
for(int i = 1; i <= n; i++) scanf("%d", &f[i][1]);
int u,v;
while(scanf("%d%d", &v, &u) && u + v){
addEdge(u, v);
}
memset(used, false, sizeof(used));
int ans = -inf;
for(int u = 1; u <= n; u++){
if(!used[u]) dfs(u);
ans = max(ans, max(f[u][0], f[u][1]));
}
printf("%d\n", ans);
}
}
Computer HDU - 2196

题意
给定一棵树,求树上每个点能到达的最远距离
思路
看了题解,跪了 orz
首先定义DP状态dp[u][0]为从u点往下走的最大距离,dp[u][1]为从u点往下走的次大距离,dp[u][2]为从u点往上走的最大距离,那么显然最终的答案就是max(dp[u][0], dp[u][2]),同时引入标记tag[u] = v,表示v出现在u往下走的最大距离中,那么
dp[u][0] = max(dp[v][0] + w),往下走的最大距离是从孩子节点中选dp[v][0]加上边权最大的
dp[u][1]随dp[u][0]是否更新而更新(这部分具体看代码)
dp[v][2] = max(dp[u][2], tag[u] ? dp[u][1] : dp[u][0]) + w,往上走的最大距离要么从父节点u往上走加边权得到(往上走),要么从父节点往下走的最大距离或次大距离得到(先往上再往下),如果tag[u]为1说明u出现在dp[u][0]中,会导致往会走,所以只能取dp[u][1]
前两条DP方程和最后一条获取的方向不同,故需要两遍DFS
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
using namespace std;
const int N = 10000 + 15;
const int inf = 0x3f3f3f3f;
const double eps = 1e-6;
typedef long long ll;
struct edge{
int v, nxt, w;
};
edge e[N << 1];
int head[N];
int tot;
int dp[N][3], tag[N];
inline void init(){
memset(head, -1, sizeof(head));
memset(dp, 0, sizeof(dp));
memset(tag, 0, sizeof(tag));
tot = 0;
}
inline void addEdge(int u, int v, int w){
e[tot] = edge{v, head[u], w};
head[u] = tot++;
}
int dfs1(int u, int pre){
dp[u][0] = dp[u][1] = dp[u][2] = tag[u] = 0;
for(int i = head[u]; ~i; i = e[i].nxt){
int v = e[i].v;
if(v == pre) continue;
int res = dfs1(v, u) + e[i].w;
if(dp[u][0] < res){
dp[u][1] = dp[u][0];
dp[u][0] = res;
tag[u] = v;
}else if(dp[u][1] < res){
dp[u][1] = res;
}
}
return dp[u][0];
}
void dfs2(int u, int pre){
for(int i = head[u]; ~i; i = e[i].nxt){
int v = e[i].v;
if(v == pre) continue;
if(v == tag[u]) dp[v][2] = max(dp[u][2], dp[u][1]) + e[i].w;
else dp[v][2] = max(dp[u][2], dp[u][0]) + e[i].w;
dfs2(v, u);
}
}
int main(){
int n;
while(~scanf("%d", &n)){
init();
for(int i = 2; i <= n; i++){
int v, w;
scanf("%d%d", &v, &w);
addEdge(i, v, w);
addEdge(v, i, w);
}
dfs1(1, -1);
dfs2(1, -1);
for(int i = 1; i <= n; i++){
printf("%d\n", max(dp[i][0], dp[i][2]));
}
}
}
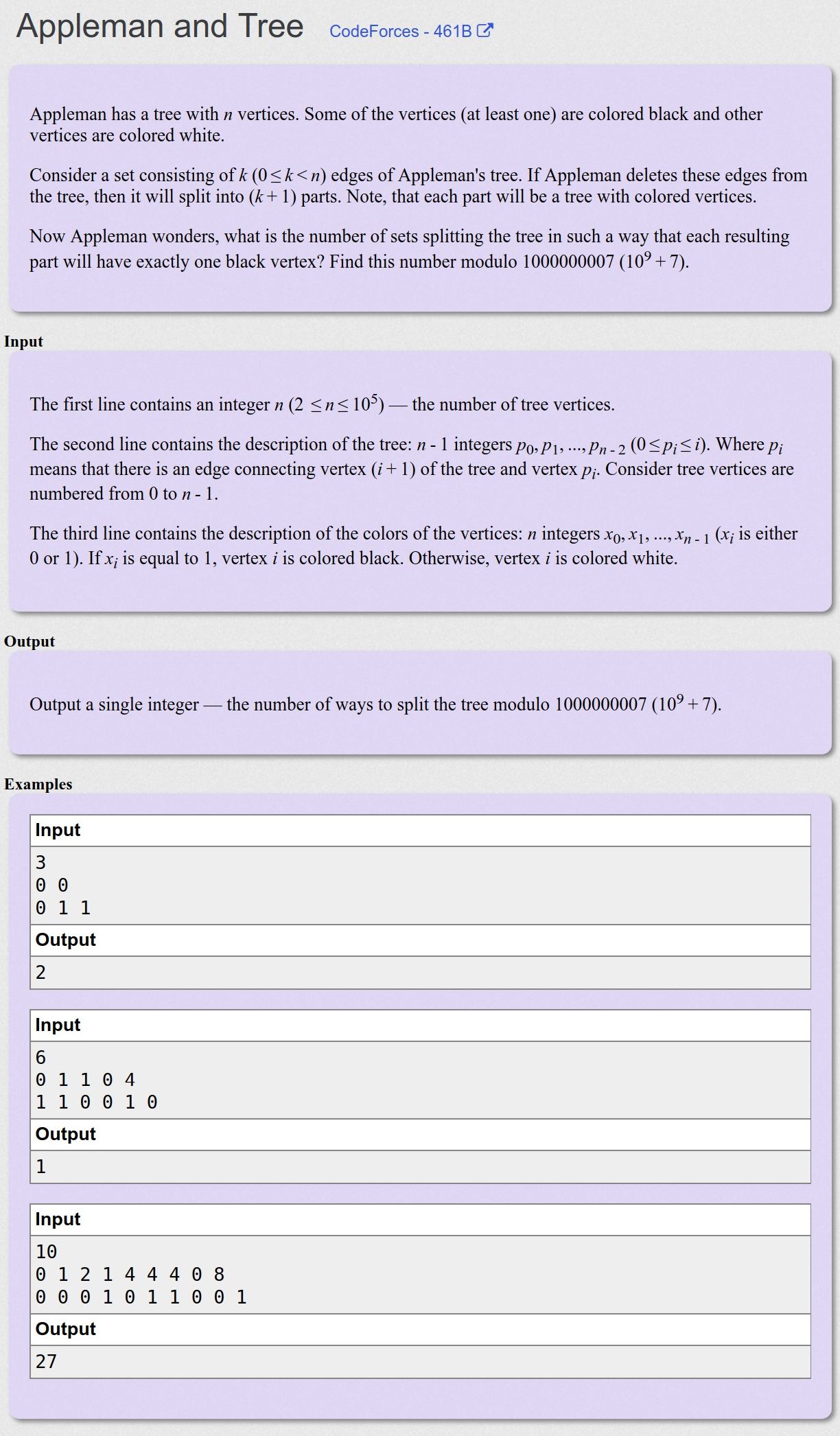
Appleman and Tree - CodeForces - 461B
题意
给定一棵树,其中的点有黑的也有白的,问去掉边后使得每个联通块只有一个黑点的方案数
思路
继续不会做,翻了一下题解 qwq
定义DP状态dp[u][0]代表以u的根的联通块中没有黑点的方案数,dp[u][1]代表以u为根的连通块中有一个黑点的方案数,则
dp[u][1] = ((dp[u][1] * dp[v][0]) + (dp[u][0] * dp[v][1]) + (dp[u][1] * dp[v][1])),则若u有黑点v没有则接上,若u没黑点v有那也接上,都有则割开
dp[u][0] = ((dp[u][0] * dp[v][0]) + (dp[u][0] * dp[v][1])),则若u无黑点v无黑点则接上,u无黑点v有则割开
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
using namespace std;
const int N = 100000 + 15;
const int inf = 0x3f3f3f3f;
typedef long long ll;
const ll MOD = 1000000007;
struct edge{
int v, nxt;
};
edge e[N << 1];
int head[N];
int tot;
ll dp[N][2];
int tag[N];
inline void init(){
memset(head, -1, sizeof(head));
tot = 0;
}
inline void addEdge(int u, int v){
e[tot] = edge{v, head[u]};
head[u] = tot++;
}
void dfs(int u, int pre){
dp[u][0] = (tag[u] == 0);
dp[u][1] = (tag[u] == 1);
for(int i = head[u]; ~i; i = e[i].nxt){
int v = e[i].v;
if(v == pre) continue;
dfs(v, u);
dp[u][1] = ((dp[u][1] * dp[v][0])%MOD + (dp[u][0] * dp[v][1])%MOD + (dp[u][1] * dp[v][1])%MOD)%MOD;
dp[u][0] = ((dp[u][0] * dp[v][0])%MOD + (dp[u][0] * dp[v][1])%MOD)%MOD;
}
}
int main(){
int n;
while(~scanf("%d", &n)){
init();
for(int i = 1; i < n; i++){
int v;
scanf("%d", &v);
addEdge(i, v);
addEdge(v, i);
}
for(int i = 0; i < n; i++) scanf("%d", &tag[i]);
dfs(0, -1);
printf("%lld\n", dp[0][1]);
}
}
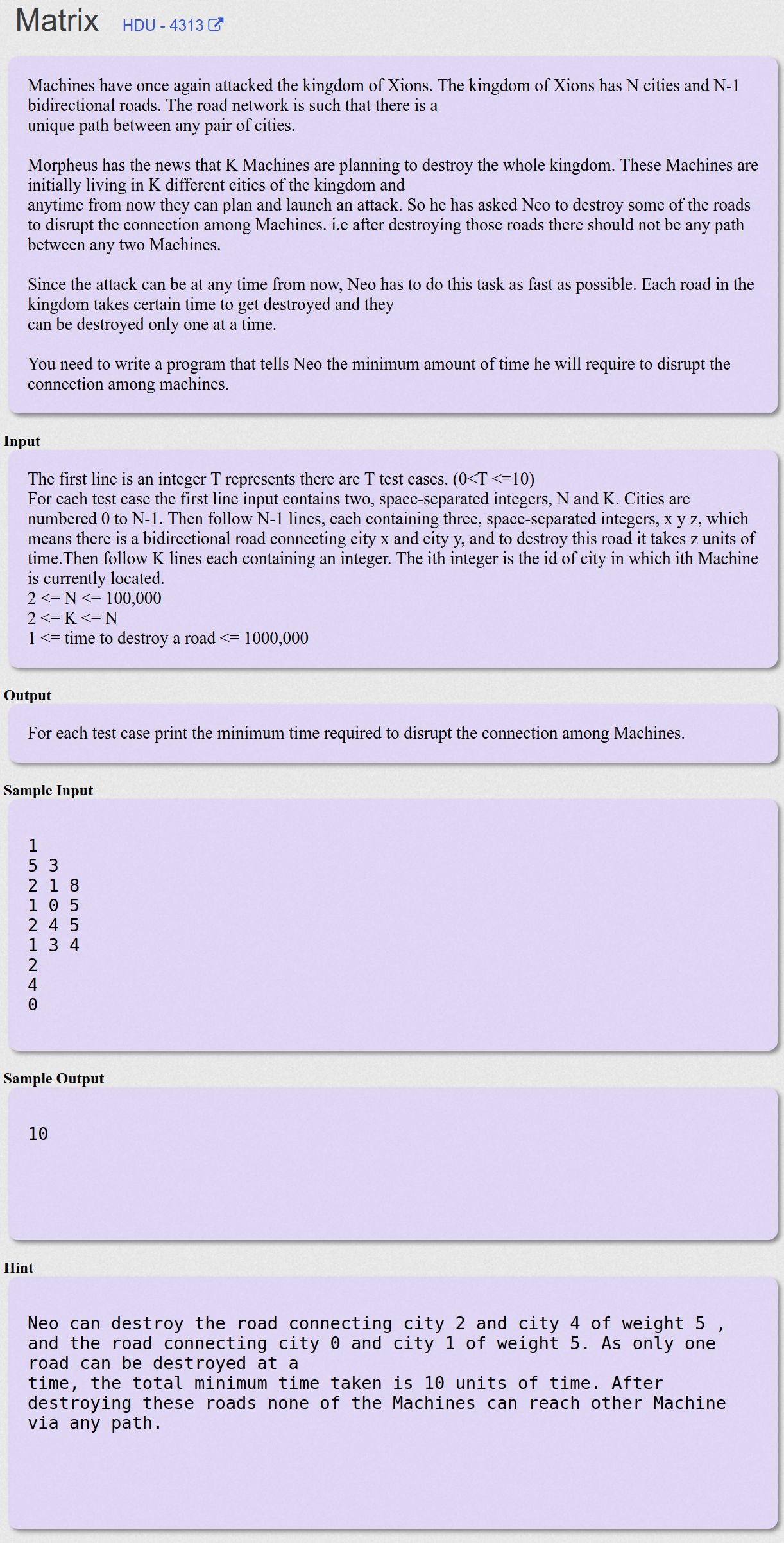
Matrix - HDU - 4313
题意
给定一棵树,其中的点有黑的也有白的,问去掉边后使得黑点不能相通的最小代价是多少
思路1 —— 树形DP
和上题很像,结果四条方程写错一条WA了一发,inf写小了WA了好几发 qwqqq
继续不会做,翻了一下题解 qwq
定义DP状态dp[u][0]代表以u的根的联通块且其中无黑点,此时的最小价值,dp[u][1]代表以u为根的连通块且其中有一个黑点,此时的最小价值,另外引入tag[u]代表u该点是否有黑点,则
当tag[u]为0时,
dp[u][1] = min(dp[u][0] - min(dp[v][0], dp[v][1] + e[i].w) + dp[v][1]),即把其中一个v的连通块换成感染的
dp[u][0] = sum(min(dp[v][0], dp[v][1] + e[i].w)),要么不割,要么割开
当tag[u]为1时,
dp[u][1] = sum(min(dp[v][0], dp[v][1] + e[i].w)),要么不割,要么隔开
dp[u][0] = inf
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
using namespace std;
const int N = 100000 + 15;
typedef long long ll;
const ll MOD = 1000000007;
const ll inf = 1LL << 45;
struct edge{
int v, nxt, w;
};
edge e[N << 1];
int head[N];
int tot;
ll dp[N][2];
int tag[N];
inline void init(){
memset(head, -1, sizeof(head));
memset(tag, 0, sizeof(tag));
tot = 0;
}
inline void addEdge(int u, int v, int w){
e[tot] = edge{v, head[u], w};
head[u] = tot++;
}
void dfs(int u, int pre){
if(tag[u]) dp[u][0] = inf, dp[u][1] = 0;
else dp[u][1] = inf, dp[u][0] = 0;
for(int i = head[u]; ~i; i = e[i].nxt){
int v = e[i].v;
if(v == pre) continue;
dfs(v, u);
if(tag[u]){
dp[u][1] += min(dp[v][0], dp[v][1] + e[i].w);
}else{
dp[u][0] += min(dp[v][0], dp[v][1] + e[i].w);
}
}
for(int i = head[u]; ~i; i = e[i].nxt){
int v = e[i].v;
if(v == pre) continue;
if(!tag[u]){
dp[u][1] = min(dp[u][1], dp[u][0] - min(dp[v][0], dp[v][1] + e[i].w) + dp[v][1]);
}
}
}
int main(){
int t;
scanf("%d", &t);
while(t--){
init();
int n, k;
scanf("%d%d", &n, &k);
for(int i = 1; i <= n - 1; i++){
int u, v, w;
scanf("%d%d%d", &u, &v, &w);
addEdge(u, v, w);
addEdge(v, u, w);
}
while(k--){
int u;
scanf("%d", &u);
tag[u] = 1;
}
dfs(0, -1);
printf("%lld\n", min(dp[0][1], dp[0][0]));
}
}
思路2 —— 贪心,Kruskal MST思想
按边权从大到小排序,然后如果两个连通块都是黑点则加上价值,否则相连
个人认为这样做的正确性在于,先把大的边权丢出去,如果一开始就遇到两个都是黑点,那么无论如何都得割开,否则能够先把大的边权拿去扩大连通块,就剩下小的边权的边不得不割开了
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
using namespace std;
const int N = 100000 + 15;
typedef long long ll;
const ll MOD = 1000000007;
const ll inf = 1LL << 45;
struct edge{
int u, v, w;
bool operator < (const edge& b) const{ return w > b.w; }
};
edge e[N];
int ft[N];
int tag[N];
inline void init(int n){
for(int i = 0; i < n; i++) ft[i] = i;
memset(tag, 0, sizeof(tag));
}
int find(int x){ return ft[x] == x ? x : ft[x] = find(ft[x]); }
void merge(int x, int y){
int p = find(x), q = find(y);
if(p != q) ft[q] = p;
}
int main(){
int t;
scanf("%d", &t);
while(t--){
int n, k;
scanf("%d%d", &n, &k);
int m = n - 1;
init(n);
for(int i = 0; i < m; i++){
scanf("%d%d%d", &e[i].u, &e[i].v, &e[i].w);
}
while(k--){
int u;
scanf("%d", &u);
tag[u] = 1;
}
sort(e, e + m);
ll ans = 0;
for(int i = 0; i < m; i++){
int u = e[i].u, v = e[i].v;
if(tag[find(u)] && tag[find(v)]){
ans += e[i].w;
}else if(tag[find(u)]){
merge(u, v);
}else{
merge(v, u);
}
}
printf("%lld\n", ans);
}
}


