线性筛、积性函数、Mobius反演
前言
不得不说这次意外地因为要啃Mobius反演而对以前学习的欧拉筛有了更深刻的理解
不过杜教筛只能等到下次学习了再更新了 qwq
因为思路是所有题目写完后才来重新推导的,所以会有一些划掉的地方,望各位dalao谅解 qwq
- 莫比乌斯反演
http://codeforces.com/blog/entry/53925
https://blog.sengxian.com/algorithms/mobius-inversion-formula - 线性筛与积性函数
https://wenku.baidu.com/view/2d706761aa00b52acec7ca63.html?re=view
Gcd - HYSBZ - 2818
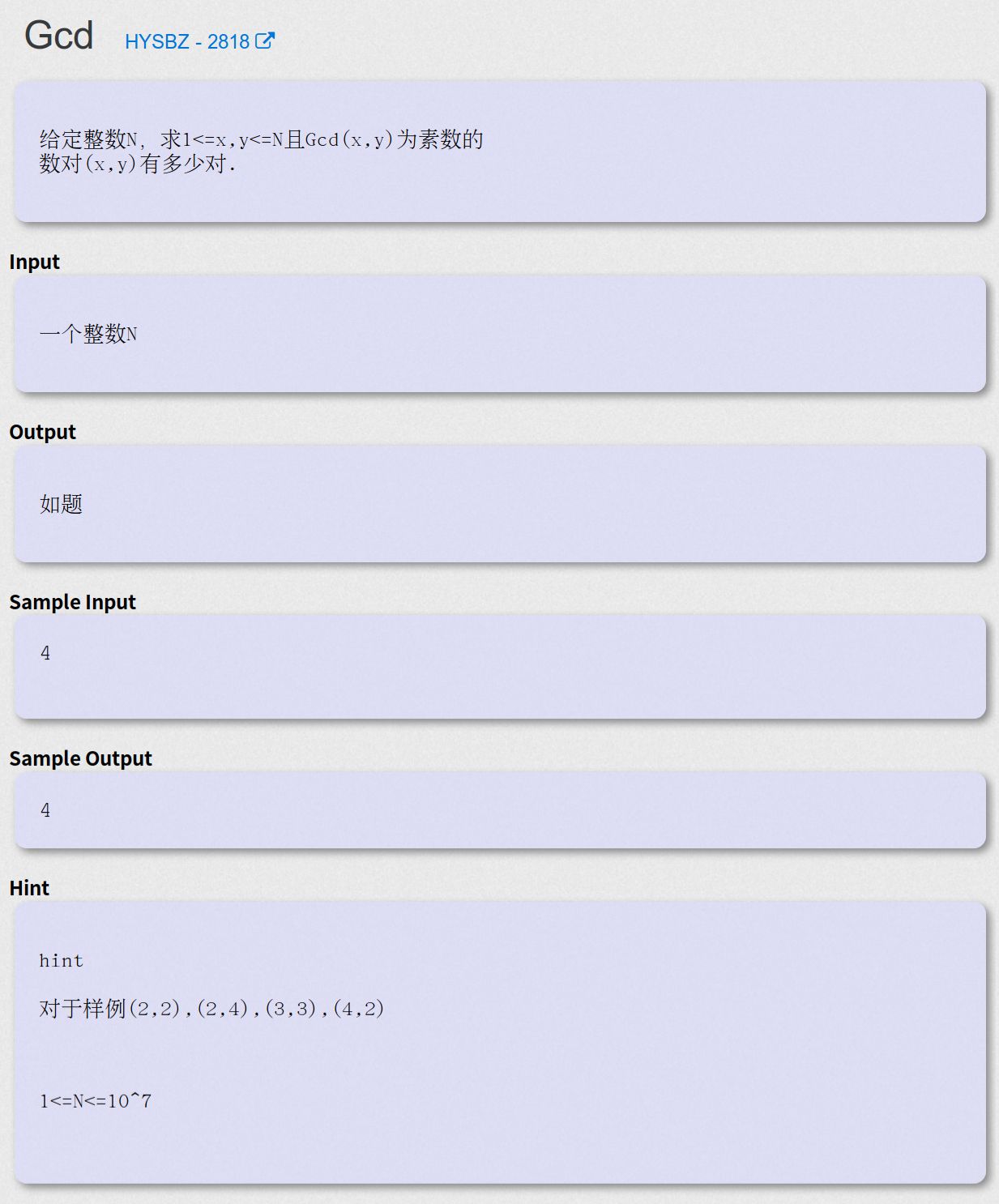
思路
#include <iostream>
#include <cstdio>
#include <list>
#include <cstring>
#include <algorithm>
#include <functional>
using namespace std;
const int N = 1e7 + 5;
const int inf = 0x3f3f3f3f;
typedef long long ll;
ll mu[N], sum[N];
bool isprime[N];
int prime[N], tot;
void init(){
memset(isprime, true, sizeof(isprime));
tot = 0, mu[1] = 1, sum[1] = 1;
for(int i = 2; i < N; i++){
if(isprime[i]){
prime[tot++] = i;
mu[i] = -1;
}
for(int j = 0; j < tot && i * prime[j] < N; j++){
isprime[i * prime[j]] = false;
if(i % prime[j] == 0){
mu[i * prime[j]] = 0;
break;
}else{
mu[i * prime[j]] = -mu[i];
}
}
sum[i] = sum[i - 1] + mu[i];
}
}
ll solve(ll n){
ll ans = 0;
for(int j = 0; j < tot && prime[j] <= n; j++){
ll p = prime[j], nn = n/p;
for(int k = 1, last = 1; k <= nn; k = last + 1){
last = nn / (nn/k);
ans += (nn/k) * (nn/k) * (sum[last] - sum[k - 1]);
}
}
return ans;
}
int main(){
init();
int n;
while(~scanf("%d", &n)){
printf("%lld\n", solve(n));
}
}
Sky - Code POJ - 3904
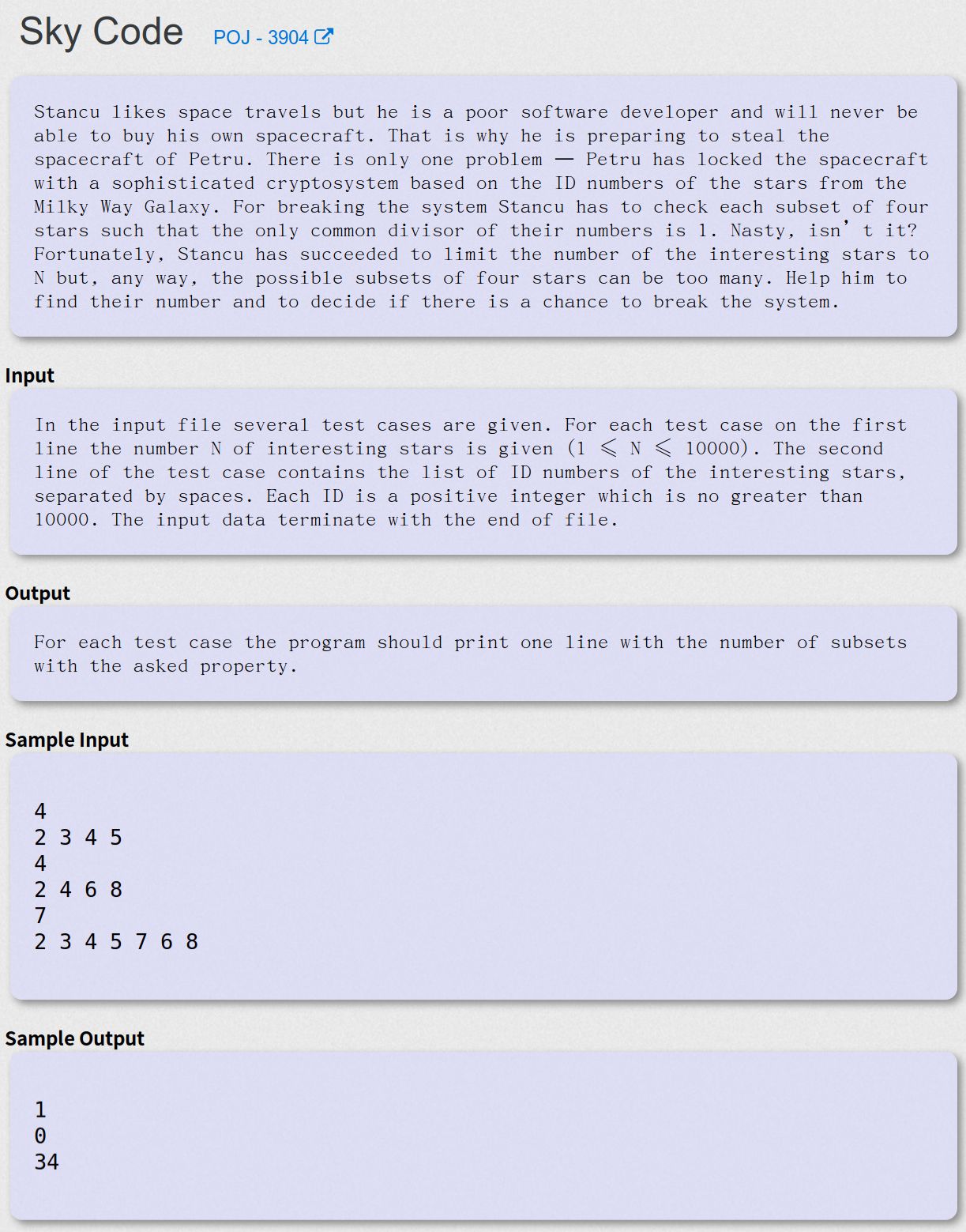
题意
给定N个数的数组ai(1 <= N <= 10000, 1 <= ai <= 10000),问从中选择4个数使其gcd为1的方案数
思路

#include <iostream>
#include <cstdio>
#include <list>
#include <cstring>
#include <algorithm>
#include <functional>
using namespace std;
const int N = 1e4 + 5;
const int inf = 0x3f3f3f3f;
typedef long long ll;
int mu[N];
int prime[N], tot;
bool isprime[N];
int num[N];
void init(){
memset(isprime, true, sizeof(isprime));
mu[1] = 1, tot = 0;
for(int i = 2; i < N; i++){
if(isprime[i]){
prime[tot++] = i;
mu[i] = -1;
}
for(int j = 0; j < tot && i * prime[j] < N; j++){
isprime[i * prime[j]] = false;
if(i % prime[j] == 0){
mu[i * prime[j]] = 0;
break;
}else{
mu[i * prime[j]] = -mu[i];
}
}
}
}
void sep(int x){
for(int i = 1; i*i <= x; i++){
if(x%i) continue;
num[i]++;
if(i*i != x) num[x/i]++;
}
}
int main(){
init();
int n;
while(~scanf("%d", &n)){
memset(num, 0, sizeof(num));
for(int i = 1; i <= n; i++){
int tmp;
scanf("%d", &tmp);
sep(tmp);
}
ll sum = 0;
for(int i = 1; i < N; i++){
if(!mu[i] || num[i] < 4) continue;
sum += (ll)mu[i] * num[i] * (num[i] - 1) * (num[i] - 2) * (num[i] - 3) / 24;
}
printf("%lld\n", sum);
}
}
Simple Sum - CodeChef - SMPLSUM
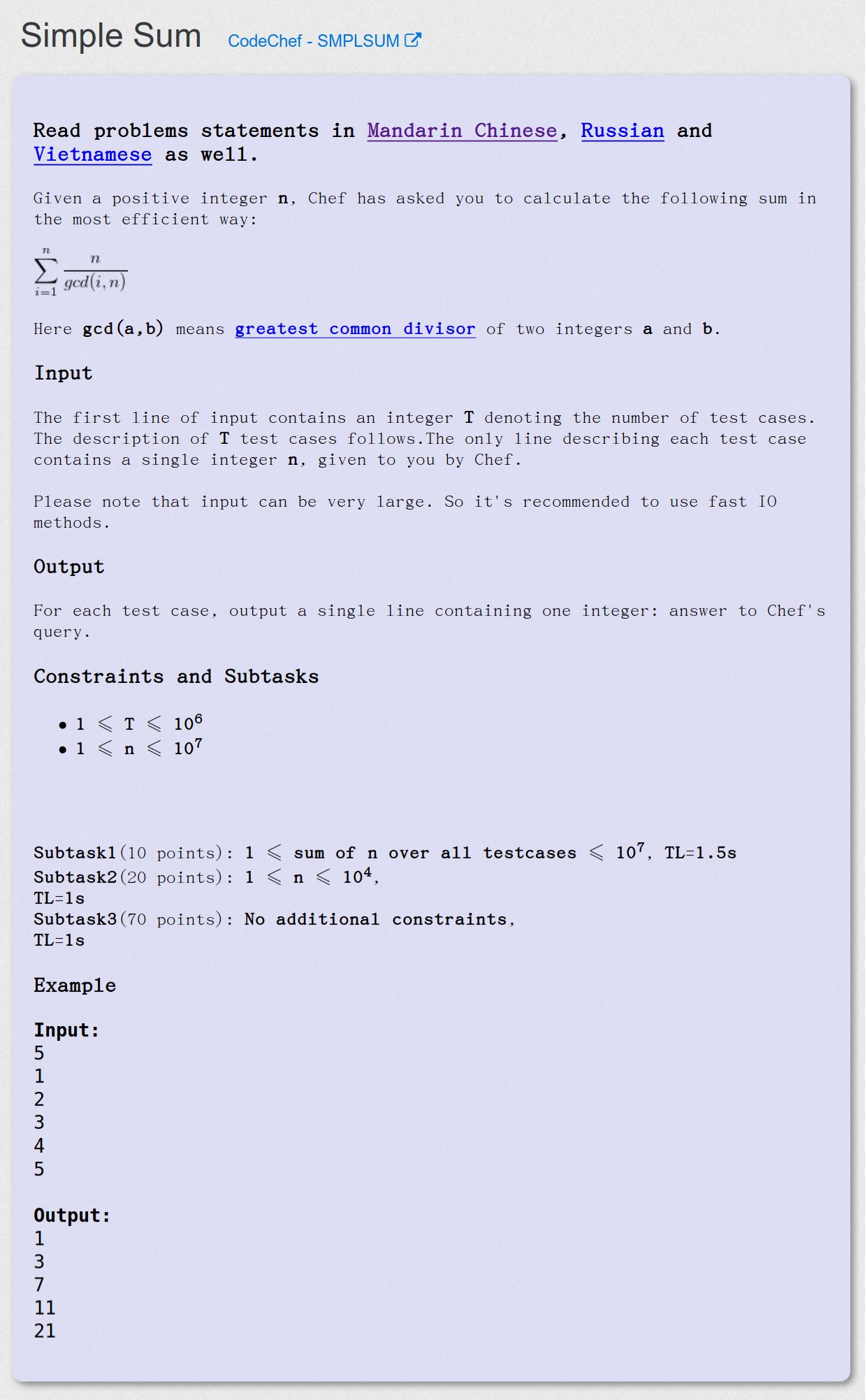
题意
多组询问求 sum(n/gcd(i, n))(i = 1 -> n) 的值
思路

#include <iostream>
#include <cstdio>
#include <list>
#include <cstring>
#include <algorithm>
#include <functional>
using namespace std;
const int N = 1e7 + 5;
const int inf = 0x3f3f3f3f;
typedef long long ll;
ll f[N];
bool isprime[N];
int prime[N], tot;
int cnt[N];
int quickPow(int a, int b){
int ans = 1, base = a;
while(b){
if(b&1) ans = ans * base;
base = base * base;
b >>= 1;
}
return ans;
}
void init(){
memset(isprime, true, sizeof(isprime));
tot = 0, f[1] = 1;
for(int i = 2; i < N; i++){
if(isprime[i]){
prime[tot++] = i;
cnt[i] = 1;
}
for(int j = 0; j < tot && (ll)i * prime[j] < N; j++){
isprime[i * prime[j]] = false;
if(i % prime[j] == 0){
cnt[i * prime[j]] = cnt[i] + 1;
break;
}else{
cnt[i * prime[j]] = 1;
}
}
}
for(int j = 0; j < tot; j++){
f[prime[j]] = (ll)prime[j] * (prime[j] - 1) + 1;
for(ll pk = prime[j], k = 1; pk * prime[j] < N; pk *= prime[j], k++){
f[pk * prime[j]] = f[pk] + (pk * prime[j]) * (pk * prime[j] - pk);
}
}
for(int i = 2; i < N; i++){
for(int j = 0; j < tot && (ll)i * prime[j] < N; j++){
if(i % prime[j] == 0){
int pk = quickPow(prime[j], cnt[i * prime[j]]);
f[i * prime[j]] = f[pk] * f[i * prime[j] / pk];
break;
}else{
f[i * prime[j]] = f[i] * f[prime[j]];
}
}
}
}
int main(){
init();
int t;
scanf("%d", &t);
while(t--){
int n;
scanf("%d", &n);
printf("%lld\n", f[n]);
}
}
Sum - ACM-ICPC 2018 南京赛区网络预赛
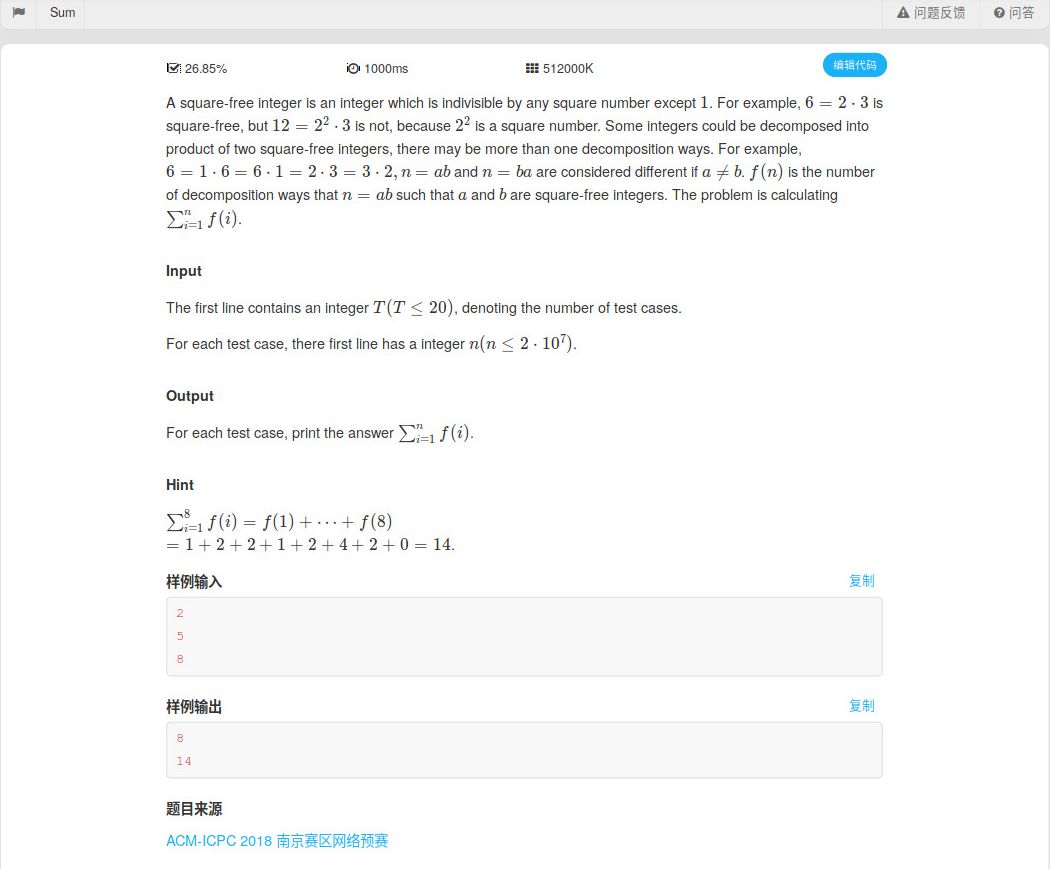
题意
定义一个数为square-free是该数无因数是平方数,定义f(i)为一个数i分解为两个数(a,b)且a和b都不是平方数的分解方案,这里(a,b)和(b,a)视为两种方案,求sum(f(i))
思路
可以知道f(i)是一个积性函数(可以打表观察出)
那么最后要解决的就是如何计算f(p^k)的问题
当k = 1时,f(p^k) = 2
当k = 2时,f(p^k) = 1
当k >= 3时,f(p^k) = 0
下面的代码差点TLE = =
#include <iostream>
#include <cstdio>
#include <list>
#include <cstring>
#include <algorithm>
#include <functional>
using namespace std;
const int N = 2e7 + 5;
const int inf = 0x3f3f3f3f;
typedef long long ll;
ll f[N], sum[N];
bool isprime[N];
int prime[N], tot;
int cnt[N];
int quickPow(int a, int b){
int ans = 1, base = a;
while(b){
if(b&1) ans = ans * base;
base = base * base;
b >>= 1;
}
return ans;
}
void init(){
memset(isprime, true, sizeof(isprime));
tot = 0, f[1] = 1, sum[1] = 1;
for(int i = 2; i < N; i++){
if(isprime[i]){
prime[tot++] = i;
cnt[i]++;
}
for(int j = 0; j < tot && i * prime[j] < N; j++){
isprime[i * prime[j]] = false;
if(i % prime[j] == 0){
cnt[i * prime[j]] = cnt[i] + 1;
break;
}else{
cnt[i * prime[j]] = 1;
}
}
}
for(int i = 0; i < tot && (ll)prime[i] * prime[i] < N; i++){
f[prime[i] * prime[i]] = 1;
ll cur = (ll)prime[i] * prime[i] * prime[i];
while(cur < N){
f[cur] = 0;
cur = cur * prime[i];
}
}
for(int i = 2; i < N; i++){
if(isprime[i]){
f[i] = 2;
}
for(int j = 0; j < tot && i * prime[j] < N; j++){
if(i % prime[j] == 0){
int pk = quickPow(prime[j], cnt[i * prime[j]]);
f[i * prime[j]] = f[pk] * f[i * prime[j] / pk];
break;
}else{
f[i * prime[j]] = f[i] * f[prime[j]];
}
}
sum[i] = f[i] + sum[i - 1];
}
}
int main(){
init();
int t;
scanf("%d", &t);
while(t--){
int n;
scanf("%d", &n);
printf("%lld\n", sum[n]);
}
}


