刷题记（回文树） —— 2018.10.3

回文树

前言

回文树用于解决字符串回文问题，个人觉得其更应该被叫做“回文自动机”
第一题的注释会写得很详细，剩下的略写

回文树
https://blog.csdn.net/lwfcgz/article/details/48739051
https://blog.csdn.net/u013368721/article/details/42100363

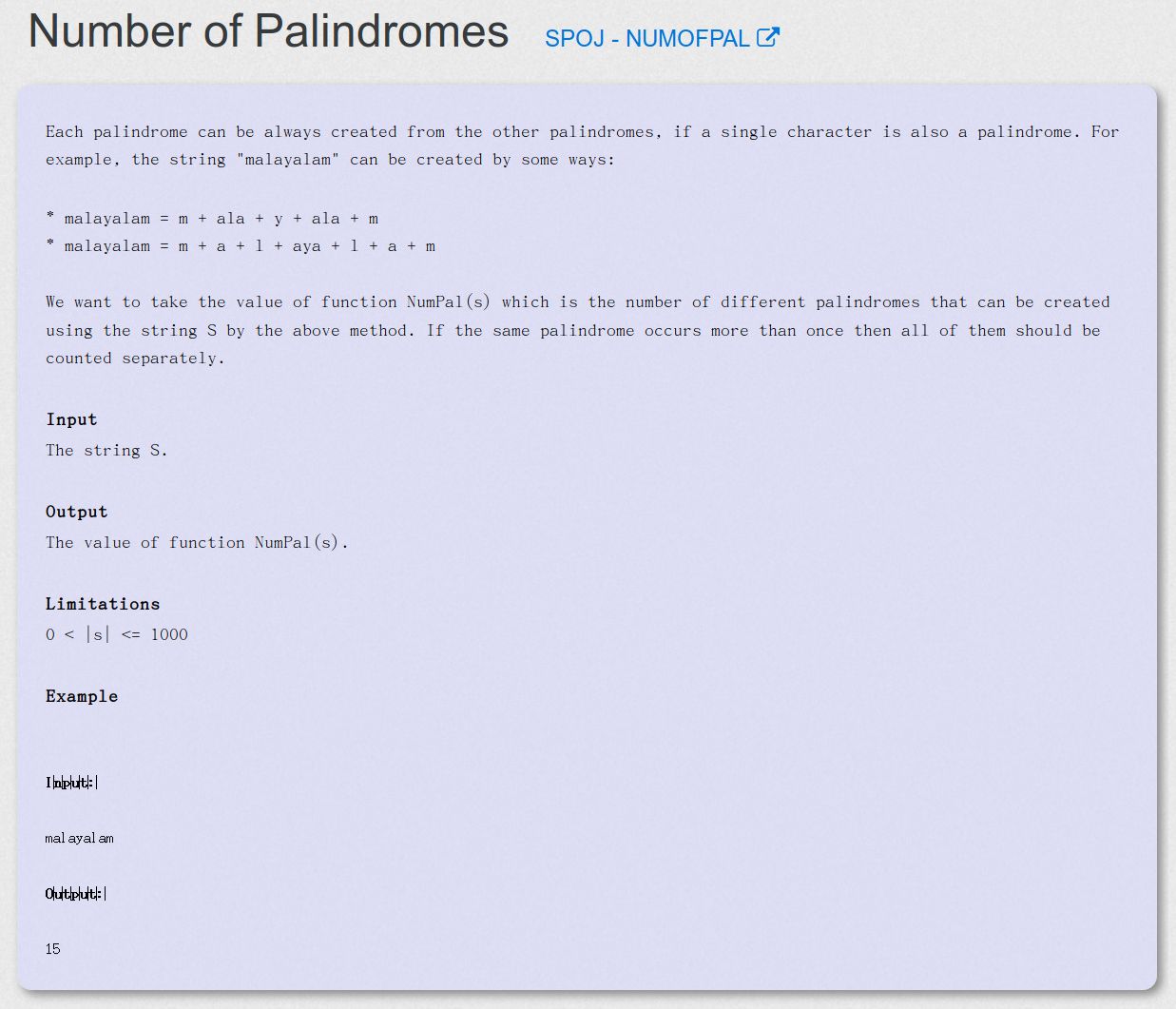
Number of Palindromes - SPOJ - NUMOFPAL

题意
求回文字符串数量
思路
回文树模板题

  #include <cstdio>
  #include <cstring>
  #include <algorithm>
  using namespace std;
  const int N = 1000 + 5;
  const int inf = 0x3f3f3f3f;
  typedef long long ll;

  char s[N];

  struct Node{
      //slink: 后缀链接
      //len: 字符串长度
      //cnt: 包括其在内的后缀字符串数量
      //nxt: nxt指针
      int slink, len, cnt;
      int nxt[26];
  };

  struct PalindromicTree{
      //tot: 静态分配
      //cursuffix: 维护当前后缀
      int  tot;
      int  cursuffix;
      Node tree[N];

      void init(){
          //长度为-1的字符串，其是不存在的，代表长度为奇数的字符串的根
          tree[0].slink = 0, tree[0].len = -1, tree[0].cnt = 1;
          //长度为0的字符串，其是空串，代表长度为偶数的字符串的根
          tree[1].slink = 0, tree[1].len = 0,  tree[1].cnt = 1;
          tot = 2, cursuffix = 1;
          initNode(1);
          initNode(0);
      }

      void initNode(int o){
          memset(tree[o].nxt, -1, sizeof(tree[o].nxt));
      }

      void add(int pos){
          int idx = s[pos] - 'a';
          int cur = cursuffix;
          //在cur的后缀链接中找到第一个可以将s[pos]接在其左右的字符串
          while(true){
              int curlen = tree[cur].len;
              if(pos - 1 - curlen >= 0 && s[pos] == s[pos - 1 - curlen])      break;
              cur = tree[cur].slink;
          }

          //如果这一字符串原本存在于后缀树中
          if(tree[cur].nxt[idx] != -1){
              //将维护的cursuffix更新为这一状态节点
              cursuffix = tree[cur].nxt[idx];
              return;
          }

          //否则，新建一状态节点
          int nxt = tree[cur].nxt[idx] = tot++;
          initNode(nxt);
          tree[nxt].len = tree[cur].len + 2;
          cursuffix = nxt;

          //如果长度为1，就不得不手动维护这一新节点的slink信息，使其指向空串
          //因为无法通过cur的后缀链接中的nxt信息来更新新节点的slink信息
          if(tree[nxt].len == 1){
              tree[nxt].cnt = 1;
              tree[nxt].slink = 1;
              return;
          }

          //如果长度大于1，就通过cur的后缀链接中第一个可以将s[pos]接在左右的字符串状态节点的nxt的节点
          //来更新新节点的slink信息
          //这一做法的正确性在于，假设当前cur节点的字符串为A，第一个满足条件的后缀链接节点代表的字符串为B，s[pos]为x
          //则xBx为xAx的后缀，又因为xAx是回文字符串，因此xBx也是xAx的前缀，那么根据循环顺序，xBx一定比xAx先处理到，
          //因此，xBx所代表的字符串节点一定是存在的，也一定是最接近于xAx的
          while(true){
              cur = tree[cur].slink;
              int curlen = tree[cur].len;
              if(pos - 1 - curlen >= 0 && s[pos] == s[pos - 1 - curlen]){
                  tree[nxt].slink = tree[cur].nxt[idx];
                  break;
              }
          }

          //更新这一后缀包含多少个回文字符串
          tree[nxt].cnt = tree[tree[nxt].slink].cnt + 1;
      }
  };

  PalindromicTree pt;

  int main(){
      pt.init();

      ll ans = 0;
      scanf("%s", s);
      for(int i = 0; s[i]; i++){
          pt.add(i);
          ans += pt.tree[pt.cursuffix].cnt;
      }
      printf("%lld\n", ans);
  }

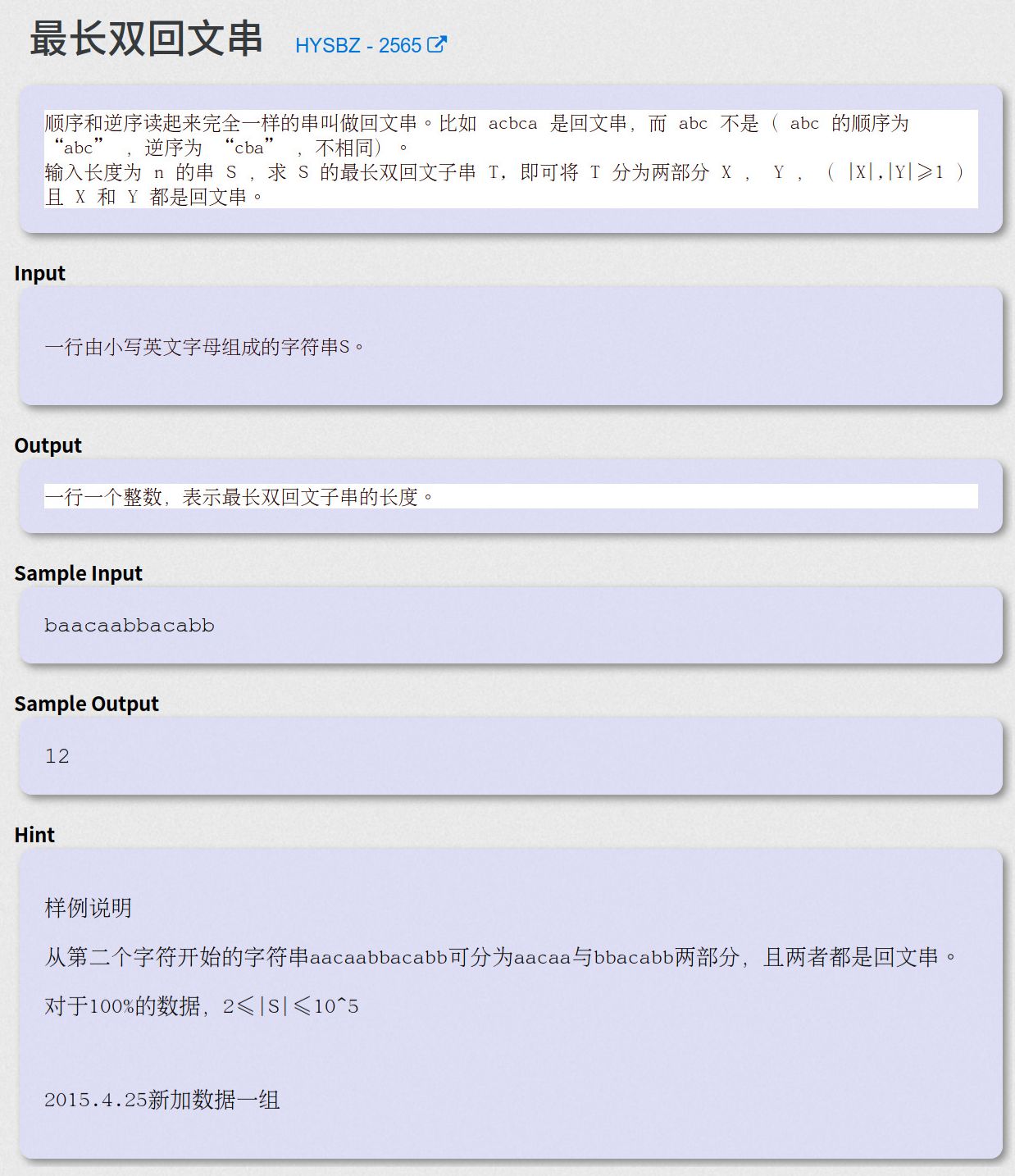
最长双回文串 - HYSBZ - 2565

思路
首先，跑一遍回文树，用数组l记录下以每个位置为右端点的回文字符串最长能是多长
然后将字符串翻转，再跑一遍回文树，用数组r记录下以每个位置为左端点的回文字符串最长能是多长
最后遍历一遍数组，取出l[i] + r[i + 1]的最大值

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1e5 + 5;
const int inf = 0x3f3f3f3f;
const int MOD = 1e9 + 7;
typedef long long ll;

char s[N];
int  l[N], r[N];

struct Node{
    int slink, len;
    int nxt[26];
};

struct PalindromicTree{
    int  cursuffix;
    Node tree[N];
    int  tot;

    void init(){
        tree[0].len = -1, tree[0].slink = 0;
        tree[1].len = 0, tree[1].slink = 0;
        initNode(0);
        initNode(1);
        tot = 2, cursuffix = 1;
    }

    void initNode(int o){
        memset(tree[o].nxt, -1, sizeof(tree[o].nxt));
    }

    void add(int pos){
        int cur = cursuffix;
        int idx = s[pos] - 'a';
        while(true){
            int curlen = tree[cur].len;
            if(pos - 1 - curlen >= 0 && s[pos] == s[pos - 1 - curlen])   break;
            cur = tree[cur].slink;
        }

        if(tree[cur].nxt[idx] != -1){
            cursuffix = tree[cur].nxt[idx];
            return;
        }

        int nxt = tree[cur].nxt[idx] = tot++;
        initNode(nxt);
        tree[nxt].len = tree[cur].len + 2;
        cursuffix = nxt;

        if(tree[nxt].len == 1){
            tree[nxt].slink = 1;
            return;
        }

        while(true){
            cur = tree[cur].slink;
            int curlen = tree[cur].len;
            if(pos - 1 - curlen >= 0 && s[pos] == s[pos - 1 - curlen]){
                tree[nxt].slink = tree[cur].nxt[idx];
                break;
            }
        }
    }
};

PalindromicTree pt;

int main(){
    while(~scanf("%s", s)){
        memset(l, 0, sizeof(l));
        memset(r, 0, sizeof(r));
        int n = strlen(s);

        pt.init();
        for(int i = 0; i < n; i++){
            pt.add(i);
            l[i] = max(l[i], pt.tree[pt.cursuffix].len);
        }

        pt.init();
        reverse(s, s + n);
        for(int i = 0; i < n; i++){
            pt.add(i);
            r[n - i - 1] = max(r[n - i - 1], pt.tree[pt.cursuffix].len);
        }

        int ans = 0;
        for(int i = 0; i < n; i++){
            if(i < n - 1)    ans = max(ans, l[i] + r[i + 1]);
            else             ans = max(ans, l[i]);
        }
        printf("%d\n", ans);
    }
}

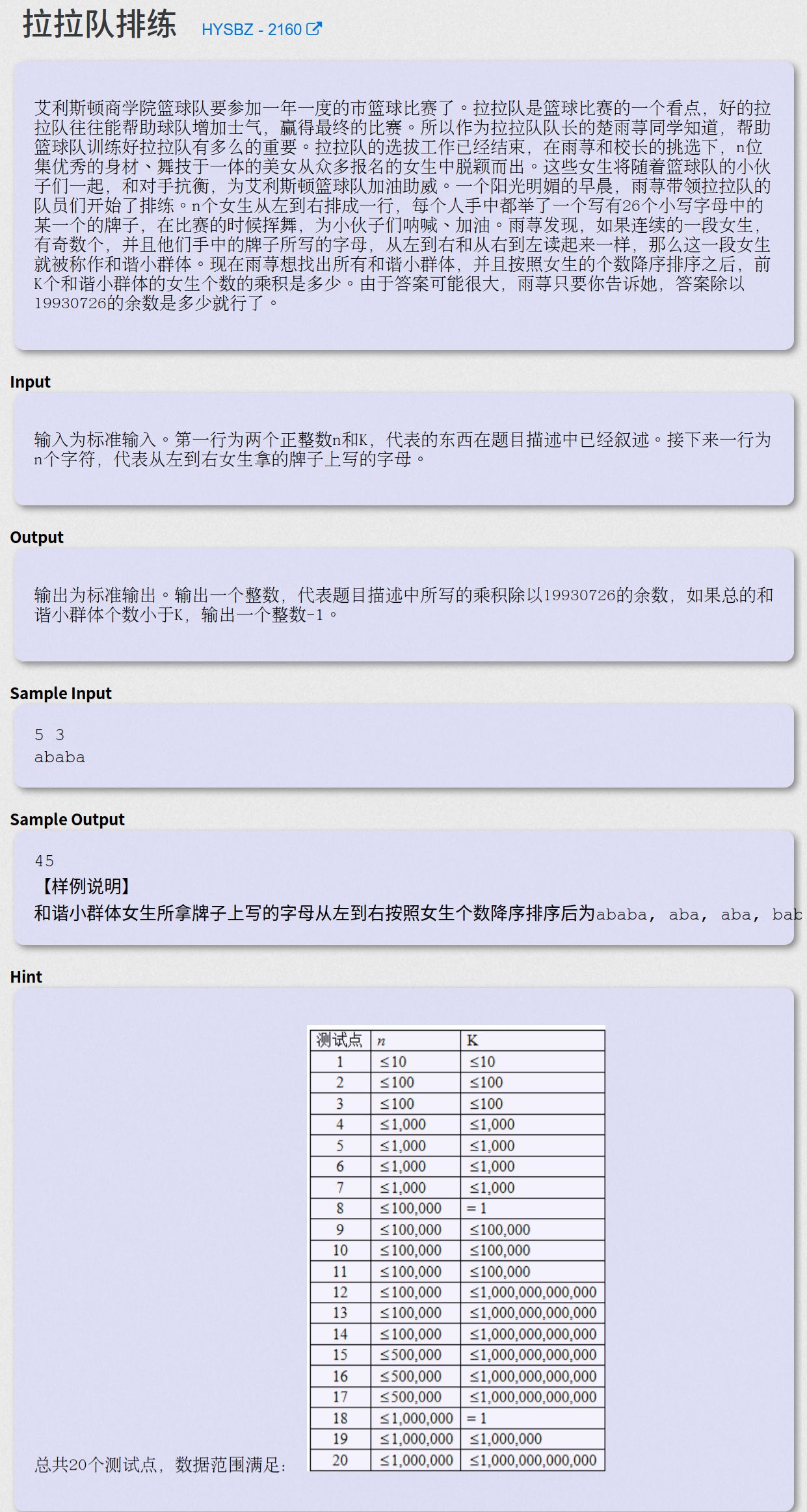
拉拉队排练 - HYSBZ - 2160

思路
首先记录下每个状态节点被访问了几次，然后用拓扑排序的思想，将这一次数通过slink向下传递，因为长的回文字符串包括短的回文字符串，然后新开一个数组，以len为下标，记录下次数，最后倒回来扫这一数组加快速幂得到答案
这里并不需要真正的拓扑排序，考虑到字符串的后缀节点必然会比该字符串节点先建立，因此只需要将静态分配的顺序倒回来扫一遍即可

  #include <cstdio>
  #include <cstring>
  #include <algorithm>
  using namespace std;
  const int N = 1e6 + 5;
  const int inf = 0x3f3f3f3f;
  const int MOD = 19930726;
  typedef long long ll;

  char s[N];
  ll   nums[N];

  ll quickPow(ll a, ll b){
      ll ans = 1, base = a;
      while(b){
          if(b&1)     ans = (ans * base) % MOD;
          base = (base * base) % MOD;
          b >>= 1;
      }
      return ans;
  }

  struct Node{
      int slink, len;
      ll  cnt;
      int nxt[26];
  };

  struct PalindromicTree{
      int  cursuffix;
      Node tree[N];
      int  tot;

      void init(){
          tree[0].len = -1, tree[0].slink = 0, tree[0].cnt = 0;
          tree[1].len = 0, tree[1].slink = 0, tree[0].cnt = 0;
          initNode(0);
          initNode(1);
          tot = 2, cursuffix = 1;
      }

      void initNode(int o){
          memset(tree[o].nxt, -1, sizeof(tree[o].nxt));
      }

      void add(int pos){
          int cur = cursuffix;
          int idx = s[pos] - 'a';
          while(true){
              int curlen = tree[cur].len;
              if(pos - 1 - curlen >= 0 && s[pos] == s[pos - 1 - curlen])   break;
              cur = tree[cur].slink;
          }

          if(tree[cur].nxt[idx] != -1){
              cursuffix = tree[cur].nxt[idx];
              tree[cursuffix].cnt++;
              return;
          }

          int nxt = tree[cur].nxt[idx] = tot++;
          initNode(nxt);
          tree[nxt].len = tree[cur].len + 2;
          tree[nxt].cnt = 1;
          cursuffix = nxt;


          if(tree[nxt].len == 1){
              tree[nxt].slink = 1;
              return;
          }

          while(true){
              cur = tree[cur].slink;
              int curlen = tree[cur].len;
              if(pos - 1 - curlen >= 0 && s[pos] == s[pos - 1 - curlen]){
                  tree[nxt].slink = tree[cur].nxt[idx];
                  break;
              }
          }
      }

      void getCnt(){
          for(int i = tot - 1; i >= 2; i--){
              tree[tree[i].slink].cnt += tree[i].cnt;
          }
      }
  };

  PalindromicTree pt;

  int main(){
      int n;
      ll k;
      while(~scanf("%d%lld%s", &n, &k, s)){
          pt.init();
          for(int i = 0; s[i]; i++){
              pt.add(i);
          }
          pt.getCnt();

          ll ans = 1;
          memset(nums, 0, sizeof(nums));
          for(int i = 2; i < pt.tot; i++){
              nums[pt.tree[i].len] += pt.tree[i].cnt;
          }

          bool flag = false;
          for(int i = N - 2; i > 0; i -= 2){
              ll tmp = min(nums[i], k);
              k -= tmp;
              ans = ans * quickPow(i, tmp) % MOD;
              if(k == 0){
                  flag = true;
                  break;
              }
          }

          if(flag)    printf("%lld\n", ans);
          else        puts("-1");
      }
  }

Palisection - CodeForces - 17E

题意
求相交的回文字符串对数量
思路
正反跑两遍回文树，得到以i为左端点的字符串数量l[i]，以及以i为右端点的字符串数量r[i]，于是答案等于总回文字符串对 - 不相交的回文字符串对，其中不相交回文字符串对为 sum(l[i] * (g[i + 1] + +g[i + 2] + ... + g[n]))
本题莫名卡内存，需要把nxt数组设为vector，以时间换空间

  #include <cstdio>
  #include <cstring>
  #include <algorithm>
  #include <vector>
  #include <unordered_map>
  #include <iostream>
  using namespace std;
  const int N = 2e6 + 5;
  const int inf = 0x3f3f3f3f;
  const int MOD = 51123987;
  typedef long long ll;

  char s[N];
  vector<int> l;

  struct Node{
      int slink, len, cnt;
      vector<pair<int, int> > nxt;
  };

  struct PalindromicTree{
      int  cursuffix;
      vector<Node> tree;
      int  tot;

      void init(){
          tree.clear();
          tree.resize(2);
          tree[0].len = -1, tree[0].slink = 0;
          tree[1].len = 0, tree[1].slink = 0;
          tot = 2, cursuffix = 1;
      }

      int nxtFind(int u, int idx){
          for(int i = 0; i < tree[u].nxt.size(); i++){
              if(tree[u].nxt[i].first == idx)   return i;
          }
          return -1;
      }

      void add(int pos){
          int cur = cursuffix;
          int idx = s[pos] - 'a';
          while(true){
              int curlen = tree[cur].len;
              if(pos - 1 - curlen >= 0 && s[pos] == s[pos - 1 - curlen])   break;
              cur = tree[cur].slink;
          }

          int tmp = nxtFind(cur, idx);
          if(tmp != -1){
              cursuffix = tree[cur].nxt[tmp].second;
              return;
          }

          int nxt = tot++;
          tree[cur].nxt.push_back(make_pair(idx, nxt));
          tree.emplace_back(Node());
          tree[nxt].len = tree[cur].len + 2;
          cursuffix = nxt;

          if(tree[nxt].len == 1){
              tree[nxt].slink = 1;
              tree[nxt].cnt = 1;
              return;
          }

          while(true){
              cur = tree[cur].slink;
              int curlen = tree[cur].len;
              if(pos - 1 - curlen >= 0 && s[pos] == s[pos - 1 - curlen]){
                  tree[nxt].slink = tree[cur].nxt[nxtFind(cur, idx)].second;
                  break;
              }
          }
          tree[nxt].cnt = tree[tree[nxt].slink].cnt + 1;
      }
  };

  PalindromicTree pt;

  int main(){
      int n;
      while(~scanf("%d%s", &n, s)){
          l.clear();

          pt.init();
          reverse(s, s + n);
          for(int i = 0; i < n; i++){
              pt.add(i);
              l.push_back(pt.tree[pt.cursuffix].cnt);
              if(i > 0)   l[i] = (l[i] + l[i - 1]) % MOD;
          }
          reverse(l.begin(), l.end());
          reverse(s, s + n);

          ll ans = ((ll)l[0] * (l[0] - 1)) % MOD * 25561994LL % MOD;
          pt.init();
          for(int i = 0; i < n; i++){
              pt.add(i);
              if(i < n - 1)   ans = ((ans - (ll)pt.tree[pt.cursuffix].cnt * l[i + 1]) % MOD + MOD) % MOD;
          }

          printf("%lld\n", ans);
      }
  }