“字节跳动杯”2018中国大学生程序设计竞赛-女生专场 - I
前言
女生专场的题目也不简单哇_(:з」∠)_
签到题跳过不写
另外感谢小姐姐推的歌~
Search for Answer - HDU - 6445

Link
https://cn.vjudge.net/problem/HDU-6297
Solution: 竞赛图 + 最小费用最大流
本题对于本蒟蒻来说,属于看了题解才懂怎么做,可能稍微变形一下就不会了的题目 QAQ
任意取四个点构成四元组(a, b, c, d),会发现有三种情况
- 成环,贡献为+1
- 有一个点出度为2,贡献为0
- 有两个点出度为2,贡献为-1
任取四个点当然难以快速计算,于是要想办法将他们拆分出来
现在假设任取四个点,都能产生正贡献,于是答案ans为A(n, 4),那么情况2的贡献就为-1,情况3的贡献就为-2
现在考虑包含某一点的情况2的情况,假设目前的边都是已经确定方向的,那么首先任取一点u,再任取两点已它出发的边的另一个端点,最后再在剩余点中任取一个点,可知方案数为
其中odg(u)为u的出度,由于给出的代码是会重复取这四个点的,只是在四元组中的位置不一样,因此对于答案的贡献值应为
\[8(n - 3)C_{odg(u)}^2 = 4(n-3)A_{odg(u)}^2\]对于情况3,会发现其已经被情况2算完了,故不需要再考虑
不知道你发现了没有,正因为前面先计算了没有贡献的情况,使得情况2和情况3被化减了,十分奇妙
因此若所有的边都确定方向,那么最终答案为
现在的问题是,如何处理那些没有确定方向的边呢
假设目前确定了y条边,使得点u的出度增加了y,那么由
可知,多出来的边的贡献为
\[\sum\limits_{i=0}^{y-1}{(odg(u)+i)}\]现在考虑如何确定这些边的方向,首先对一条边,其只能使其中一个点的出度增大,这一增大的出度的贡献值由它是第几条边决定
于是若把边列为一排,点视为一排,对于每条还没确定方向的边,分别添加两条由该边指向两个端点的流量为1,费用0的边,再从源点src添加若干条流量为1,费用为0的边连接边,最后由从1到n的点向汇点des连接若干条边
对于每一个从1到n的点,每条连接到汇点des的边的权值应为odg(u), odg(u) + 1, ..., odg(u) + idg(u) - 1,这是由上述公式决定的
那么最后由最小费用最大流可知,当这幅图满流时,所有的边都会选择完毕,而且都会优先选择令
最小化的边,正是题目所需要的
因此本题的最终答案为
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
typedef long long ll;
const int N = 450 + 15;
const int inf = 0x3f3f3f3f;
struct edge {
int v, val, cost, next;
};
edge e[N * N * 2];
int tot, head[N], pre[N], d[N], cur[N];
bool inq[N];
int odg[N], idg[N];
int G[N][N];
inline void init() {
memset(odg, 0, sizeof(odg));
memset(idg, 0, sizeof(idg));
memset(head, -1, sizeof(head));
tot = 0;
}
inline void addEdge(int u, int v, int val, int cost) {
e[tot] = edge{v, val, cost, head[u]};
head[u] = tot++;
e[tot] = edge{u, 0, -cost, head[v]};
head[v] = tot++;
}
bool spfa(int src, int des) {
queue<int> que;
memset(d, 0x3f, sizeof(d));
memset(inq, false, sizeof(inq));
d[src] = 0, pre[src] = src;
que.push(src);
inq[src] = true;
while(!que.empty()) {
int u = que.front();
que.pop();
inq[u] = false;
for(int i = head[u]; ~i; i = e[i].next) {
int v = e[i].v;
if(d[v] > d[u] + e[i].cost && e[i].val) {
d[v] = d[u] + e[i].cost;
pre[v] = u;
cur[v] = i;
if(!inq[v]) {
que.push(v);
inq[v] = true;
}
}
}
}
return d[des] != inf;
}
int flow(int src, int des) {
int ans = 0;
while(spfa(src, des)) {
int aug = inf;
for(int v = des; v != src; v = pre[v]) aug = min(aug, e[cur[v]].val);
for(int v = des; v != src; v = pre[v]) {
e[cur[v]].val -= aug;
e[cur[v]^1].val += aug;
}
ans += d[des] * aug;
}
return ans;
}
inline int solve(int n){
int pe = n, src = 0, des = 0;
for(int i = 1; i <= n; i++) {
for(int j = i + 1; j <= n; j++) {
if(G[i][j] != 2) continue;
addEdge(++pe, i, 1, 0);
addEdge(pe, j, 1, 0);
addEdge(src, pe, 1, 0);
idg[i]++;
idg[j]++;
}
}
des = ++pe;
for(int i = 1; i <= n; i++) {
for(int cnt = 0; cnt < idg[i]; cnt++) {
addEdge(i, des, 1, odg[i] + cnt);
}
}
return flow(src, des) * (n - 3) * 8;
}
int main() {
int t;
scanf("%d", &t);
while(t--) {
init();
int n;
scanf("%d", &n);
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= n; j++) {
int tmp;
scanf("%1d", &tmp);
G[i][j] = tmp;
if(tmp == 1) odg[i]++;
}
}
int ans = n * (n - 1) * (n - 2) * (n - 3);
//printf("A_n^4 = %d\n", ans);
for(int i = 1; i <= n; i++) {
ans -= odg[i] * (odg[i] - 1) * (n - 3) * 4;
}
//printf("now ans = %d\n", ans);
printf("%d\n", ans - solve(n));
}
}
SA-IS后缀数组 - HDU - 6294

链接
https://cn.vjudge.net/problem/HDU-6294
思路 —— DP
有点像DP,但是的确用了DP思维
首先字典序大小看首位,若首位都相同,那么字典序大小就由第二位决定,以此类推,那么若定义suf(i)与suf(i+1)的字典序大小关系为dp(i),则
- 当
s[i] == s[i+1]时,dp(i) = dp(i+1) - 当
s[i] != s[i+1]时,dp(i)由字母大小决定
另外就是要注意初值,dp(n - 1)必然是>,因为s[n]无字符
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <map>
#include <algorithm>
using namespace std;
typedef long long ll;
const int N = 1000000 + 15;
inline int read() {
int x = 0; static char c; bool minus = false;
for (; !(c >= '0' && c <= '9'); c = getchar()) if (c == '-') minus = true;
for (; c >= '0' && c <= '9'; x = x * 10 + c - '0', c = getchar()); if (minus) x = -x;
return x;
}
char s[N];
char ans[N];
int main(){
int t = read();
while(t--){
int n = read();
scanf("%s", s);
ans[n - 1] = '>';
for(int i = n - 2; i >= 0; i--){
if(s[i] == s[i + 1]){
ans[i] = ans[i + 1];
}else if(s[i] > s[i + 1]){
ans[i] = '>';
}else{
ans[i] = '<';
}
}
printf("%.*s\n", n - 1, ans);
}
}
缺失的数据范围 - HDU - 6288

链接
https://cn.vjudge.net/problem/HDU-6288
思路 —— 二分
裸的二分,然而要用__int128,学到了
(虽说是开挂做法)
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <vector>
using namespace std;
using it = __int128;
typedef unsigned long long ull;
typedef long long ll;
const int N = 1e5 + 15;
const int inf = 0x3f3f3f3f;
inline char get(void) {
static char buf[1000000], *p1 = buf, *p2 = buf;
if (p1 == p2) {
p2 = (p1 = buf) + fread(buf, 1, 1000000, stdin);
if (p1 == p2) return EOF;
}
return *p1++;
}
inline ll read() {
ll x = 0; static char c; bool minus = false;
for (; !(c >= '0' && c <= '9'); c = get()) if (c == '-') minus = true;
for (; c >= '0' && c <= '9'; x = x * 10 + c - '0', c = get()); if (minus) x = -x;
return x;
}
char WritellBuffer[1024];
template <typename T>
inline void write(T a,char end){
ll cnt=0,fu=1;
if(a<0){putchar('-');fu=-1;}
do{WritellBuffer[++cnt]=fu*(a%10)+'0';a/=10;}while(a);
while(cnt){putchar(WritellBuffer[cnt]);--cnt;}
if(end) putchar(end);
}
bool check(ull n, ull k, ull a, ull b){
it ans = 1;
for(int i = 1; i <= a; i++){
ans *= n;
if(ans > k) return false;
}
it tmp = ceil(log2(n));
for(int i = 1; i <= b; i++){
ans *= tmp;
if(ans > k) return false;
}
return true;
}
int main(){
int t = read();
while(t--){
ull a = read(), b = read(), k = read();
ull l = 1, r = 1e18, ans = 1;
while(l <= r){
ull m = (l + r) >> 1;
if(check(m, k, a, b)){
ans = m;
l = m + 1;
}else{
r = m - 1;
}
}
write(ans, '\n');
}
}
对称数 - HDU - 6291

链接
https://cn.vjudge.net/problem/HDU-6291
思路 —— 树上莫队 + 分块查询
莫队也许不是最快的做法,因为在Vjudge上有3000+ms就跑完的
本题用莫队维护数字出现了奇数次还是偶数次(开个数组异或即可实现),然后查询的时候就把2e5个数分成sqrt(2e5)块,查询的时候看一下哪一块还有出现偶数次的数字,有的话在进入块内暴力查询
为了方便查询哪一个块有偶数次的数字出现,还需要用莫队维护一下每一块中出现偶数次的数字的数量
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
using namespace std;
const int N = 200000 + 5;
typedef long long ll;
inline char get(void) {
static char buf[1000000], *p1 = buf, *p2 = buf;
if (p1 == p2) {
p2 = (p1 = buf) + fread(buf, 1, 1000000, stdin);
if (p1 == p2) return EOF;
}
return *p1++;
}
inline int read() {
int x = 0; static char c; bool minus = false;
for (; !(c >= '0' && c <= '9'); c = get()) if (c == '-') minus = true;
for (; c >= '0' && c <= '9'; x = x * 10 + c - '0', c = get()); if (minus) x = -x;
return x;
}
struct squery{
int u, v, idx;
};
struct edge{
int v, next;
};
squery query[N];
edge e[N << 1];
int BLOCK_SIZE;
int head[N], tot, belong[N], stk[N], pstk, fa[N][20], dpt[N];
int cnt[N], mp[N], val[N];
bool is_even[N];
int ans[N];
inline void init(){
memset(head, -1, sizeof(head));
memset(fa, -1, sizeof(fa));
memset(cnt, 0, sizeof(cnt));
memset(is_even, 1, sizeof(is_even));
tot = 0;
for(int i = 1; i < N; i++){
mp[i] = sqrt(i);
cnt[mp[i]]++;
}
}
inline void addEdge(int u, int v){
e[tot] = edge{v, head[u]};
head[u] = tot++;
}
void dfs(int u, int pre, int depth){
int bottom = pstk;
dpt[u] = depth;
for(int i = head[u]; ~i; i = e[i].next){
int v = e[i].v;
if(v == pre) continue;
fa[v][0] = u;
dfs(v, u, depth + 1);
if(pstk - bottom >= BLOCK_SIZE){
while(pstk != bottom){
belong[stk[pstk--]] = u;
}
}
}
stk[++pstk] = u;
}
void initLCA(int n){
for(int j = 1; j <= 19; j++){
for(int u = 1; u <= n; u++){
if(fa[u][j - 1] == -1) continue;
fa[u][j] = fa[fa[u][j - 1]][j - 1];
}
}
}
void initBlockAndLCA(int n){
pstk = 0;
dfs(1, -1, 0);
while(pstk >= 1){
belong[stk[pstk--]] = 1;
}
initLCA(n);
}
int getFa(int u, int v){
if(dpt[u] > dpt[v]) swap(u, v);
for(int j = 19; j >= 0; j--){
if(fa[v][j] == -1 || dpt[fa[v][j]] < dpt[u]) continue;
v = fa[v][j];
}
if(u == v) return u;
for(int j = 19; j >= 0; j--){
if(fa[v][j] == -1 || fa[u][j] == -1 || fa[u][j] == fa[v][j]) continue;
u = fa[u][j], v = fa[v][j];
}
return fa[u][0];
}
void reverse(int u){
is_even[val[u]] ^= 1;
if(is_even[val[u]]){
cnt[mp[val[u]]]++;
}else{
cnt[mp[val[u]]]--;
}
}
void moveNode(int u, int v){
while(u != v){
if(dpt[u] < dpt[v]){
reverse(v);
v = fa[v][0];
}else{
reverse(u);
u = fa[u][0];
}
}
}
int solve(){
int sz = sqrt(N);
int bk = 1;
for(int i = 1; i <= sz; i++){
if(cnt[i]){
bk = i;
break;
}
}
int l = lower_bound(mp + 1, mp + N, bk) - mp;
int r = upper_bound(mp + 1, mp + N, bk) - mp;
while(l < r){
if(is_even[l]) return l;
l++;
}
return -1;
}
int main(){
int t = read();
while(t--){
int n = read(), m = read();
init();
BLOCK_SIZE = sqrt(n);
for(int i = 1; i <= n; i++){
val[i] = read();
}
for(int i = 1; i <= n - 1; i++){
int u = read(), v = read();
addEdge(u, v);
addEdge(v, u);
}
initBlockAndLCA(n);
for(int i = 0; i < m; i++){
int u = read(), v = read();
query[i] = squery{u, v, i};
}
sort(query, query + m, [](const squery& a, const squery& b) -> bool {
return (belong[a.u] != belong[b.u] ? belong[a.u] < belong[b.u] : belong[a.v] < belong[b.v]);
});
int u = query[0].u, v = query[0].v;
moveNode(u, v);
reverse(getFa(u, v));
ans[query[0].idx] = solve();
reverse(getFa(u, v));
for(int i = 1; i < m; i++){
int nu = query[i].u, nv = query[i].v;
moveNode(u, nu);
moveNode(v, nv);
int lca = getFa(nu, nv);
reverse(lca);
ans[query[i].idx] = solve();
reverse(lca);
u = nu, v = nv;
}
for(int i = 0; i < m; i++){
printf("%d\n", ans[i]);
}
}
}
口算训练 - HDU - 6287

链接
https://cn.vjudge.net/problem/HDU-6287
思路1 —— 线段树动态开点 + 质因数分解
开1e5棵线段树,第i棵都维护在pos位置上的数字x中因子i出现的次数,维护区间和
那么查询的时候就用线段树查询区间[l, r]内数字x所含的各个因子的数量是否不超过区间所含数量
耗时2500+ms
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <unordered_map>
#define lson ch[o][0], l, m
#define rson ch[o][1], m + 1, r
using namespace std;
typedef long long ll;
const int N = 1e5 + 15;
inline char get(void) {
static char buf[1000000], *p1 = buf, *p2 = buf;
if (p1 == p2) {
p2 = (p1 = buf) + fread(buf, 1, 1000000, stdin);
if (p1 == p2) return EOF;
}
return *p1++;
}
inline int read() {
int x = 0; static char c; bool minus = false;
for (; !(c >= '0' && c <= '9'); c = get()) if (c == '-') minus = true;
for (; c >= '0' && c <= '9'; x = x * 10 + c - '0', c = get()); if (minus) x = -x;
return x;
}
int seg[N * 31 * 4];
int tot;
int ch[N * 31 * 4][2];
unordered_map<int, int> root;
inline void init(){
//memset(root, 0, sizeof(root));
root.clear();
tot = 1;
}
inline void newNode(int& o){
o = tot++;
ch[o][0] = ch[o][1] = 0;
seg[o] = 0;
}
void push(int& o, int l, int r, int pos, int val){
if(!o) newNode(o);
seg[o] += val;
if(l == r) return;
int m = (l + r) >> 1;
if(pos <= m) push(lson, pos, val);
else push(rson, pos, val);
}
int query(int o, int l, int r, int ql, int qr){
if(ql <= l && r <= qr){
return seg[o];
}
int m = (l + r) >> 1;
int ans = 0;
if(ql <= m) ans += query(lson, ql, qr);
if(m < qr) ans += query(rson, ql, qr);
return ans;
}
void pushX(int x, int idx, int n){
for(int i = 2; i <= (int)sqrt(x); i++){
if(x % i == 0){
int cnt = 0;
while(x % i == 0){
x /= i;
cnt++;
}
push(root[i], 1, n, idx, cnt);
}
}
if(x != 1){
push(root[x], 1, n, idx, 1);
}
}
bool check(int x, int l, int r, int n){
for(int i = 2; i <= (int)sqrt(x); i++){
if(x % i == 0){
int cnt = 0;
while(x % i == 0){
x /= i;
cnt++;
}
if(cnt > query(root[i], 1, n, l, r)) return false;
}
}
if(x != 1){
if(1 > query(root[x], 1, n, l, r)) return false;
}
return true;
}
int main(){
int t = read();
while(t--){
init();
int n = read(), m = read();
for(int i = 1; i <= n; i++){
int x = read();
pushX(x, i, n);
}
while(m--){
int l = read(), r = read(), x = read();
puts(check(x, l, r, n) ? "Yes" : "No");
}
}
}
思路2 —— map + 前缀和 + 质因数分解
与上题的思路类似,只是因为不需要修改所以可以用map代替线段树,序列数字因子全部处理完成后求前缀和
查询时二分左右端点查询即可
然而耗时3000+ms = =||
思路3 —— vector + 二分 + 质因数分解
用vec[i]记录因子i出现的位置,一个数字产生多个则记录多个,按顺序记录
那么查询时便可以直接二分查询左右端点[l, r]出现在vec中的区间长度,若不超过因子数则是ok的
耗时1300+ms
#include <iostream>
#include <cstdio>
#include <vector>
#include <cmath>
#include <algorithm>
using namespace std;
const int N = 1e5 + 15;
inline char get(void) {
static char buf[1000000], *p1 = buf, *p2 = buf;
if (p1 == p2) {
p2 = (p1 = buf) + fread(buf, 1, 1000000, stdin);
if (p1 == p2) return EOF;
}
return *p1++;
}
inline int read() {
int x = 0; static char c; bool minus = false;
for (; !(c >= '0' && c <= '9'); c = get()) if (c == '-') minus = true;
for (; c >= '0' && c <= '9'; x = x * 10 + c - '0', c = get()); if (minus) x = -x;
return x;
}
vector<int> vec[N];
inline void init(){
for(int i = 0; i < N; i++){
vec[i].clear();
}
}
inline void push(int x, int idx){
for(int i = 2; i <= sqrt(x); i++){
while(x % i == 0){
x /= i;
vec[i].push_back(idx);
}
}
if(x != 1){
vec[x].push_back(idx);
}
}
inline bool query(int x, int l, int r){
for(int i = 2; i <= sqrt(x); i++){
int cnt = 0;
while(x % i == 0){
x /= i;
cnt++;
}
if(cnt && upper_bound(vec[i].begin(), vec[i].end(), r) - lower_bound(vec[i].begin(), vec[i].end(), l) < cnt){
return false;
}
}
if(x != 1 && upper_bound(vec[x].begin(), vec[x].end(), r) - lower_bound(vec[x].begin(), vec[x].end(), l) < 1){
return false;
}
return true;
}
int main(){
int t = read();
while(t--){
init();
int n = read(), m = read();
for(int i = 1; i <= n; i++){
int val = read();
push(val, i);
}
while(m--){
int l = read(), r = read(), val = read();
puts(query(val, l, r) ? "Yes" : "No");
}
}
return 0;
}
代码派对 - HDU 6296
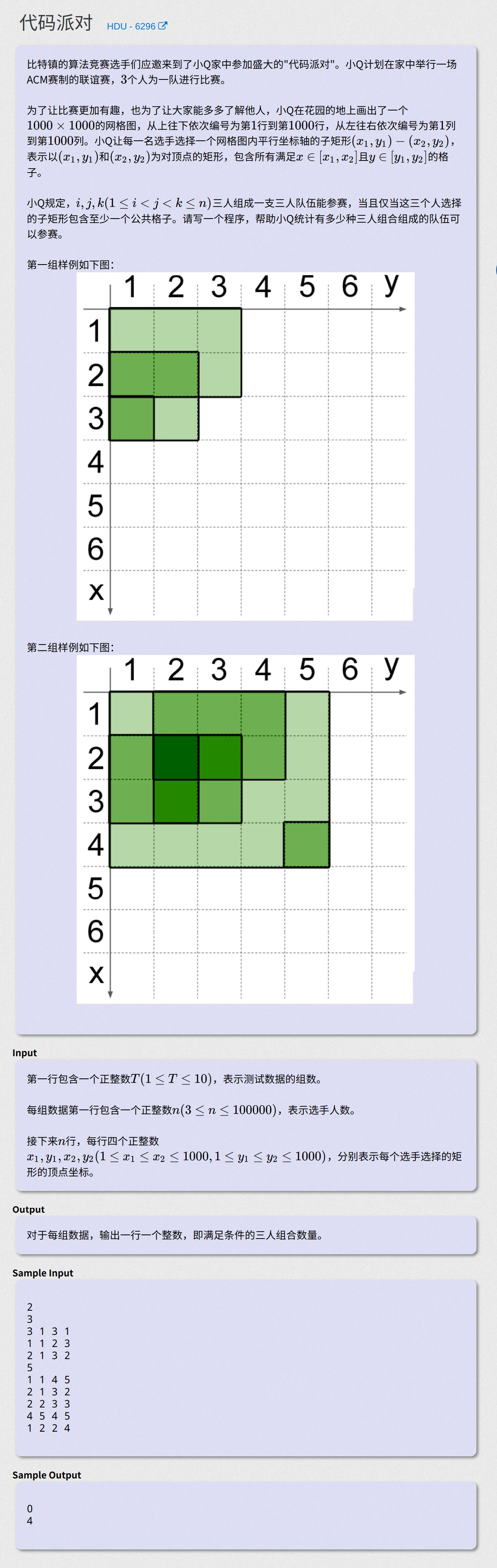
链接
https://cn.vjudge.net/problem/HDU-6296
思路 —— 二维差分 + 二维前缀和 + 容斥
这题看了好久题解才明白了QAQ
首先用二维差分与前缀和便可以计算出每个格子被矩形覆盖的次数
记 ans1 = C(num[i][j], 3),可以知道这个ans1是有重复计算的成分的
现在考虑会重复计算的原因,任取三个矩形,若他们的交集不止一个格子,那么我们计算其他格子就会重复这三个矩形的方案数,因此对于每三个矩形产生交集,若我们能只计算其中一个格子,就可以避免重复计算。从感性的角度来讲,我们当然更乐意选择边角的格子,本蒟蒻在实现中选择的是左上角
要只计算交集左上角的格子对这三个矩形组成的这一种方案数的贡献,而忽略交集中其他格子的贡献,我们自然会想到容斥。如何容斥呢,产生交集的必然是三个矩形的边界,若我们将所有矩形的左边往右缩进一格,交集的左边界自然会被往右缩进一格,此时计算方案数ans2,同理将所有矩形的上边往下缩进一格,计算方案数ans3,容易知道ans2和ans3中已经包含了其他格子对于这三个矩形组成的方案数的贡献,而不含左上角格子的贡献,因此我们可以ans1 - ans2 - ans3,但是不含左上角格子的右下区域被重复删去了两次,因此我们将所有矩形的左边往右缩进一格,同时上边往下缩进一格,得到ans4,再加上去即可
因此,最终方案数为ans1 - ans2 - ans3 + ans4
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
typedef long long ll;
const int N = 1005;
const int M = 100000 + 15;
inline int read() {
int x = 0; static char c; bool minus = false;
for (; !(c >= '0' && c <= '9'); c = getchar()) if (c == '-') minus = true;
for (; c >= '0' && c <= '9'; x = x * 10 + c - '0', c = getchar()); if (minus) x = -x;
return x;
}
int input_x[M][3], input_y[M][3];
int G[N][N];
inline ll solve(int m, int dx, int dy){
memset(G, 0, sizeof(G));
for(int i = 1; i <= m; i++){
int x1 = input_x[i][1] + dx, x2 = input_x[i][2];
int y1 = input_y[i][1] + dy, y2 = input_y[i][2];
if(x1 > x2 || y1 > y2) continue;
G[x1][y1]++;
G[x1][y2 + 1]--;
G[x2 + 1][y1]--;
G[x2 + 1][y2 + 1]++;
}
ll ans = 0;
for(int i = 1; i < N; i++){
for(int j = 1; j < N; j++){
G[i][j] = G[i][j] + G[i - 1][j] + G[i][j - 1] - G[i - 1][j - 1];
//printf("%5d", G[i][j]);
ans += (ll)G[i][j] * (G[i][j] - 1) * (G[i][j] - 2) / 6;
}
//puts("");
}
//puts("---");
return ans;
}
int main(){
int t = read();
while(t--){
int m = read();
for(int i = 1; i <= m; i++){
input_x[i][1] = read(), input_y[i][1] = read();
input_x[i][2] = read(), input_y[i][2] = read();
if(input_x[i][1] > input_x[i][2]) swap(input_x[i][1], input_x[i][2]);
if(input_y[i][1] > input_y[i][2]) swap(input_y[i][1], input_y[i][2]);
}
printf("%lld\n", solve(m, 0, 0) - solve(m, 1, 0) - solve(m, 0, 1) + solve(m, 1, 1));
}
}


