CodeForces 669D, CodeForces 570B
题
会做的题:
- (水题)Cows and Poker Game —— CodeForces - 284B
http://codeforces.com/problemset/problem/284/B - (水题)Guest From the Past —— CodeForces - 625A
http://codeforces.com/problemset/problem/625/A - (水题)Simple Game —— CodeForces - 570B
http://codeforces.com/problemset/problem/570/B - Little Artem and Dance —— CodeForces - 669D
http://codeforces.com/problemset/problem/669/D
不会做的题:
- Buy Low Sell High —— CodeForces - 867E
http://codeforces.com/problemset/problem/867/E
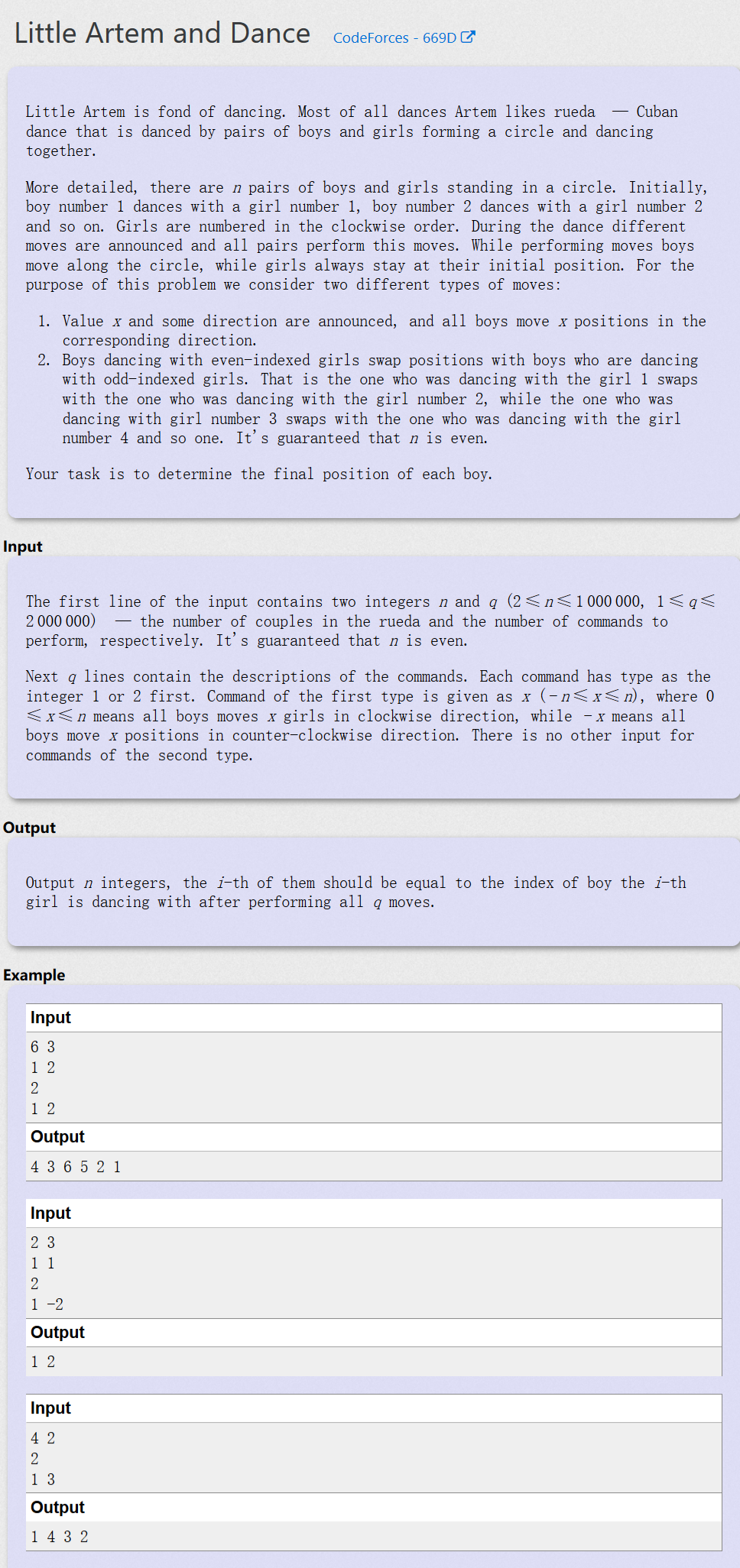
Little Artem and Dance —— CodeForces - 669D
 思路
思路
题目大意是给定一个圈圈上有N个点,N为偶数,他们的位置顺时针记为1,2,3,……,N,同时一开始每个位置上的值等于它们自身的位置的值,现在给定两种操作,第一种操作是将圈上所有值都顺时针走x个单位或逆时针走x个单位,第二种操作是将位置1和2, 3和4, 5和6, ……, n-1和n上的值进行互换,请输出q次给定操作后圆圈从位置1顺时针顺序开始的所有的值。在样例输入中,1代表操作1, x代表顺时针走x个单位,-x代表逆时针走x个单位,2代表操作2
首先注意范围分别是 n <= 1e6, q <= 2e6, 模拟全部过程妥妥TLE,但是又要输出最后的结果,而且给定的操作都是随机的,因此我们需要想一个能够部分模拟或者不模拟方法来计算出最后的结果。首先 对于所有点,操作1对于他们都是相同的,因此每次的操作1都可以累加结果, 对于操作2, 题干的交换其实可以理解为 奇数位置的点+1, 偶数位置的点-1, 因此其实只需要模拟一遍一开始在位置1的点的整个过程, 就能够计算出对于所有奇数点和偶数点最后的位置
一开始本来想用 k^=tmp 优化,没想到WA了,改成 k = (k + tmp)%2 就AC了,似乎是位运算不能接受那么大的数 QAQ
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;
const int N = 1000005;
ll op_tot[2] = {0}; // [0]为奇数点最后移动的距离,[1]为偶数点最后移动的距离
ll ans[N];
int main(){
ll n, q, op, tmp;
ll k = 1; // 位置1的点
scanf("%lld%lld", &n, &q);
for(int i = 0; i < q; i++){
scanf("%lld", &op);
if(op&1){
scanf("%lld", &tmp);
while(tmp < 0) tmp += n;
k = (k + tmp)%2; //为了方便计算奇偶,可以假设k在一个2个点的圈子里面
op_tot[1] = (op_tot[1] + tmp)%n; //%n只是为了防止溢出
op_tot[0] = (op_tot[0] + tmp)%n;
}else{
if(k){ //k如果此时走到奇数位置
op_tot[1] = (op_tot[1] + 1)%n; //所有的奇数点就+1
op_tot[0] = (op_tot[0] - 1 + n)%n; //对应的偶数点就-1,下同
}else{
op_tot[1] = (op_tot[1] - 1 + n)%n;
op_tot[0] = (op_tot[0] + 1)%n;
}
k ^= 1; //交换位置后,奇数变偶数位置,偶数位置变奇数位置
}
}
for(int i = 1; i <= n; i++){
ans[(i - 1 + op_tot[i&1])%n + 1] = i;
}
for(int i = 1; i <= n; i++){
printf((i < n ? "%lld " : "%lld\n"), ans[i]);
}
return 0;
}
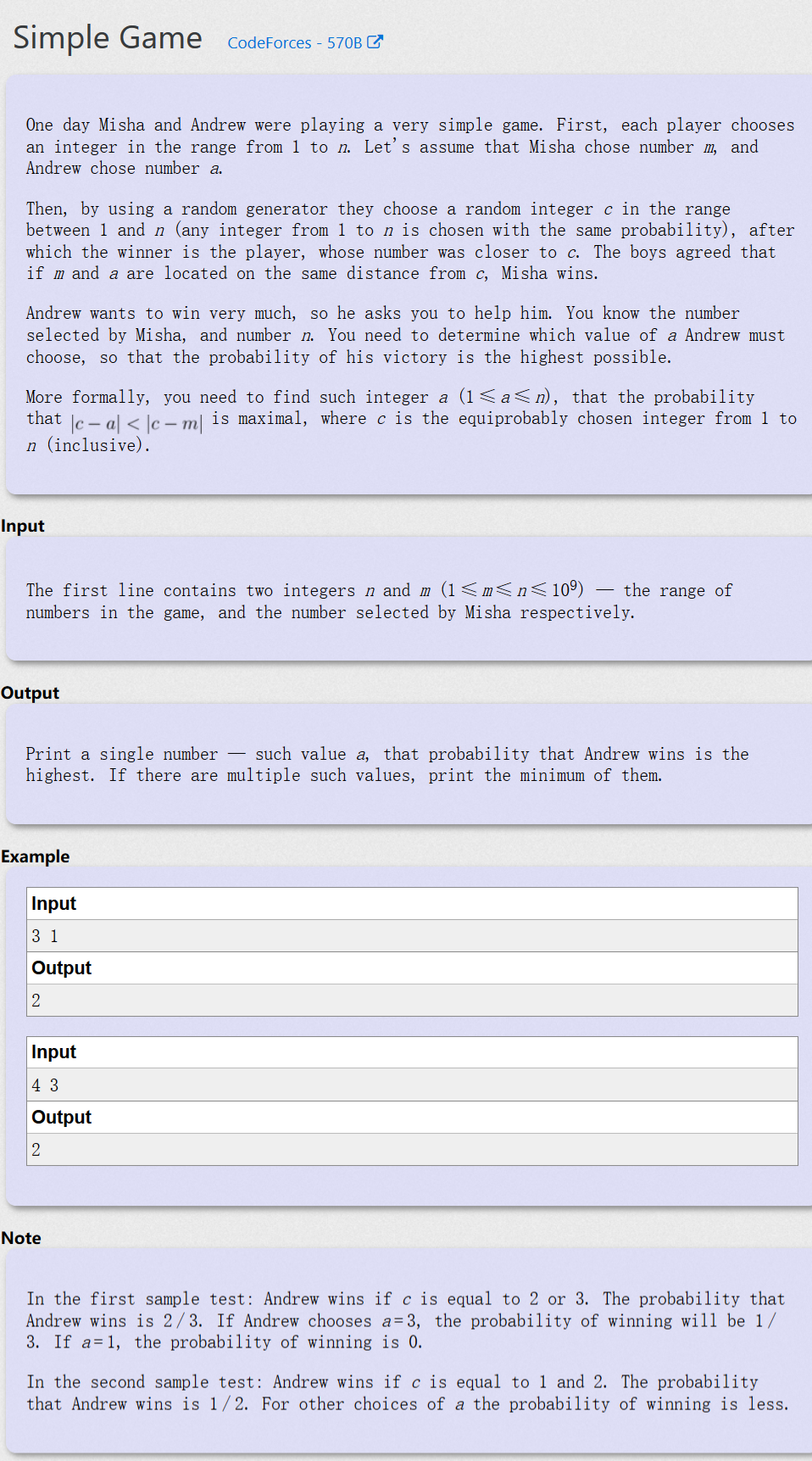
Simple Game —— CodeForces - 570B
 思路
思路
题目大意为,给定一行整数1,2,……,N,已知N,给定一个数m,现有任意一整数点c在区间[1,N]上,求在区间[1,N]上的一整数点a,使其满足|c - a| < |c - m|的概率最大
本题其实蛮水的,不难发现,当m离某一端点更远时,在那一边取离m最近的点就能满足题意,即 a = m - 1 >= n - m ? m - 1 : m + 1,然后就非常漂亮的WA了 T^T
本题还挖了个坑,当 n == 1 且 m == 1 时, 因为只有m这一个点,所以a只能取1,需要特判一下
#include <iostream>
using namespace std;
int main(){
ios::sync_with_stdio(false);
int n, m;
cin >> n >> m;
if(n == 1 && m == 1){
cout << 1 << endl;
}else{
cout << (m - 1 >= n - m ? m - 1 : m + 1) << endl;
}
return 0;
}


