扩展欧几里德 | CodeForces 898B, CodeForces 599B
前言
最近课业繁重 + 养病就一直没时间和精力更新,个人觉得那些没有标明是水题的和我自己不会做的是有价值看的题,至于水题嘛连我自己都觉得水就别说各位大佬了
然后以后的刷题记会针对某一算法来展开,单纯训练思维的题目会减少
然后这个系列呢, 立个flag, 至少30篇
题
会做的题:
- (水题)Spotlights | CodeForces - 729B
http://codeforces.com/problemset/problem/729/B - (水题)Tea Party | CodeForces - 808C
http://codeforces.com/problemset/problem/808/C - (水题)Polo the Penguin and Strings | CodeForces - 289C
http://codeforces.com/problemset/problem/289/C - (水题)Increase and Decrease | CodeForces - 246B
http://codeforces.com/problemset/problem/246/B - (水题)Pocket Book | CodeForces - 152C
http://codeforces.com/problemset/problem/152/C - (水题)Dishonest Sellers | CodeForces - 779C
http://codeforces.com/problemset/problem/779/C - (水题)Div. 64 | CodeForces - 887A
http://codeforces.com/problemset/problem/887/A - Spongebob and Joke | CodeForces - 599B
http://codeforces.com/problemset/problem/599/B - Slava and tanks | CodeForces - 877C
http://codeforces.com/problemset/problem/877/C - Proper Nutrition | CodeForces - 898B
http://codeforces.com/problemset/problem/898/B - Chloe and the sequence | CodeForces - 743B
http://codeforces.com/problemset/problem/743/B
不会做的题:
- Timofey and rectangles | CodeForces - 763B
http://codeforces.com/problemset/problem/763/B - New Year Book Reading | CodeForces - 500C
http://codeforces.com/problemset/problem/500/C - Bug in Code | CodeForces - 421D
http://codeforces.com/problemset/problem/421/D - Game of the Rows | CodeForces - 839B
http://codeforces.com/problemset/problem/839/B
Proper Nutrition | CodeForces - 898B
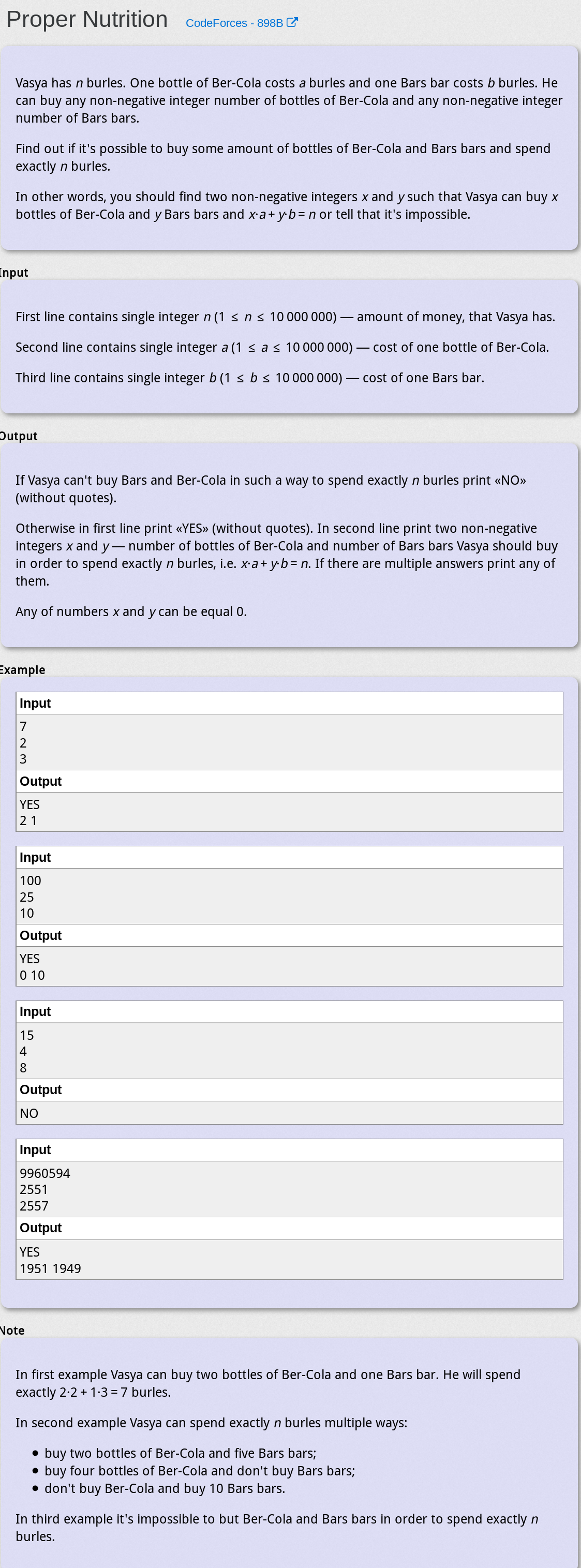 题目大意
题目大意
对于方程 ax + by = n,给定a,b,n, 求非负的x,y满足该式,无法求解输出”NO”
思路
第一种方法: 暴力(耗时140ms)
显而易见,从0开始枚举x,使得(n - a*x)%b == 0成立,到ax > n时结束枚举
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long ll;
int main(){
ll n, a, b;
while(cin >> n >> a >> b){
ll x = -1, y = -1;
for(ll i = 0; n - a*i >= 0; i++){
if((n - a*i)%b == 0){
x = i;
y = (n - a*i)/b;
}
}
if(x == -1 && y == -1){
printf("NO\n");
}else{
printf("YES\n");
printf("%lld %lld\n", x, y);
}
}
return 0;
}
第二种方法: 扩展欧几里德(耗时15ms)
没错如果只是暴力我绝对不会写题解的!
ax+by=c是标准的不定方程,可用扩展欧几里德求解,不懂扩展欧几里德算法的同学可以百度了解一下
用扩展欧几里德解不定方程我这也是第一次呢 :)
#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long ll;
ll exgcd(ll a, ll b, ll& x, ll& y){
ll d = a;
if(b == 0){
x = 1, y = 0;
}else{
d = exgcd(b, a%b, y, x); // x' = y;
y -= a/b*x; // y' = x - a/b*y;
}
return d;
}
int main(){
ll n, a, b, x, y, tmp;
while(~scanf("%lld%lld%lld", &n, &a, &b)){
tmp = __gcd(a, b);
if(n % tmp != 0){ //a,b,c一定都能除以gcd(a,b),不能除必定无解
printf("NO\n");
}else{
a /= tmp;
b /= tmp;
n /= tmp; //以上三步将方程化为 a‘x + b'y = c'
exgcd(a, b, x, y); //求解的是 a'x + b'y = 1
x = x*n; //因为求解相差c'倍所以乘上c'
x = (x%b + b)%b; //x可能为负数所以不断加上b
y = (n - a*x)/b; //再用新的x求解出y
if(y < 0){ //x是非负最小解,对于这个解y还是负数那就没解了
printf("NO\n");
}else{
printf("YES\n");
printf("%lld %lld\n", x, y);
}
}
}
return 0;
}
Spongebob and Joke | CodeForces - 599B
 题目大意
题目大意
对于方程 b(i) = f(a(i)), 给定b(i), f(i)序列求解整个a(i)序列, 如果无法求解输出“Impossible”, 有多种结果输出”Ambiguity”
思路
用数学的方法分析这一题目, 方程左右两端再加个f^(-1), 可得 f^(-1)(b(i)) = a(i), 这样子所给条件就能直接求出b(i)
这个f^(-1)是什么呢,原来f(i)是下标对应值, 那么现在f^(-1)是值对应下标,仅此而已
因此 Impossible就是f^(-1)(b(i))无对应下标, Ambiguity就是f^(-1)(b(i))有多个下标对应
用两个数组或者map存b(i)和f^(-1)就可以把整道题写出来了
另外注意 Impossible 和 Ambiguity同时成立要先输出 Impossible, 不然会WA的 T_T
#include <iostream>
#include <algorithm>
#include <cstring>
#include <map>
using namespace std;
typedef long long ll;
int cnt[N];
map<int, int> mp_f; //f^(-1)(i)
int arr[N]; //b(i)
int ans[N]; //a(i)
int ans_end;
string res(int m){
for(int i = 1; i <= m; i++){
if(cnt[arr[i]] == 0) return "Impossible";
}
for(int i = 1; i <= m; i++){
if(cnt[arr[i]] >= 2) return "Ambiguity";
ans[i] = mp_f[arr[i]];
}
return "Possible";
}
int main(){
ios::sync_with_stdio(false);
int n, m;
while(cin >> n >> m){
memset(cnt, 0, sizeof(cnt));
for(int i = 1; i <= n; i++){
int tmp;
cin >> tmp;
mp_f[tmp] = i; //值对应下标,存入f^(-1)
cnt[tmp]++; //统计值对应多个下标的可能性
if(cnt[tmp] == 1){
mp_f.insert(pii(tmp, i));
}
}
for(int i = 1; i <= m; i++){
cin >> arr[i];
}
string str = res(m);
cout << str << endl;
if(str != "Possible") continue;
for(int i = 1; i <= m; i++){
cout << ans[i];
if(i < m) cout << " ";
}
cout << endl;
}
return 0;
}


