各种背包问题
前言
背包问题真是博大精深呀,学习DP任重道远
题
不会做的题
- Balance | POJ - 1837
http://poj.org/problem?id=1837 - The Values You Can Make | CodeForces - 687C
http://codeforces.com/problemset/problem/687/C
看了题解的题
- Dima and Salad | CodeForces - 366C
http://codeforces.com/problemset/problem/366/C
Homer Simpson | UVA 10465
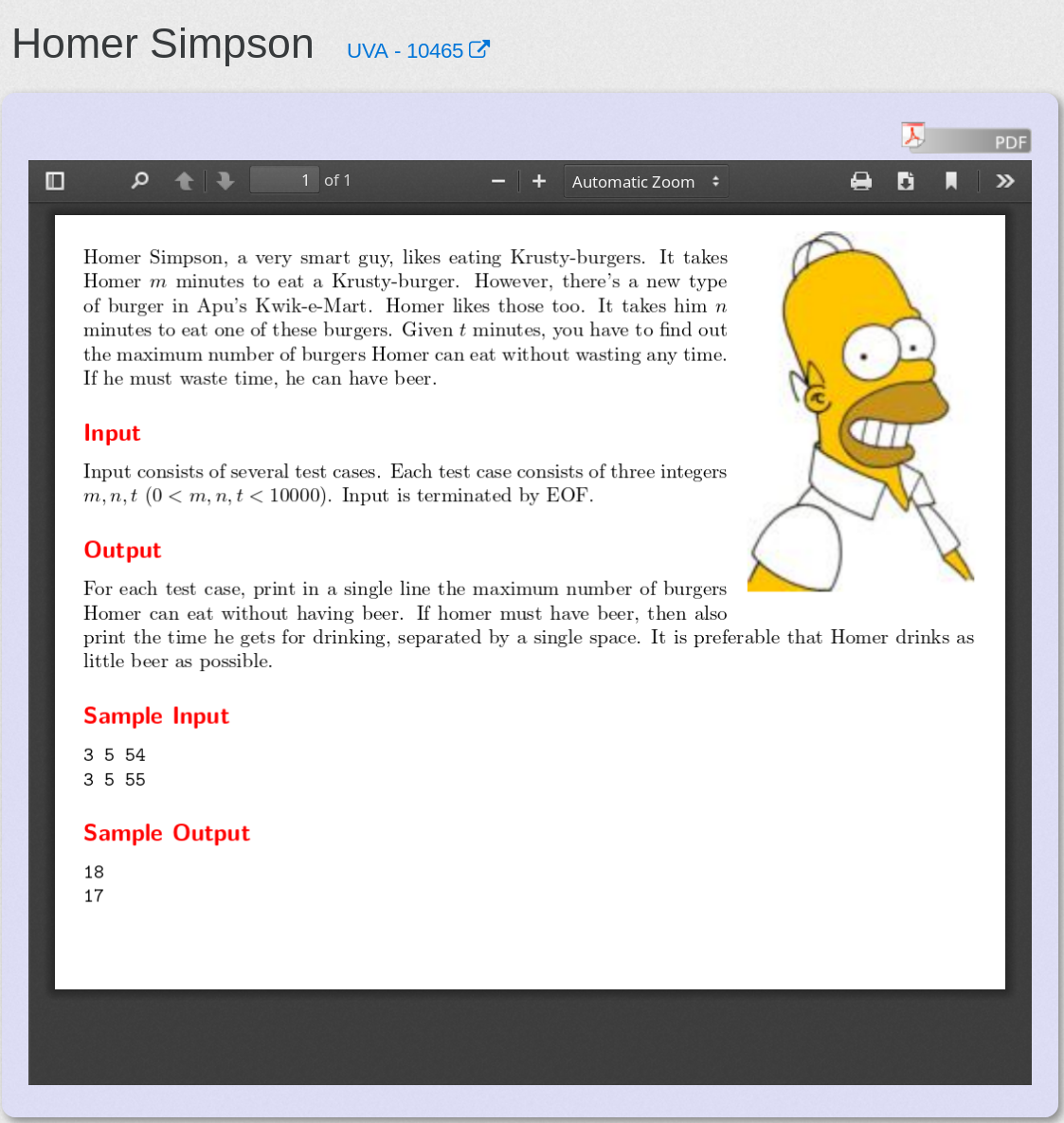 题目大意
题目大意
有两种汉堡,一种吃一个要用m分钟,另一种要n分钟,现在给t分钟,求在这个时间内在尽量不要有时间剩余的前提下,最多能吃多少汉堡,如果必须有时间剩余则也输出剩下多少时间
思路
目测是 完全背包问题,将时间作为物体的重量,数量作为物品的价格。
题目要求尽量不要有时间剩余,所以求的是背包容量满时的最优解,应将dp的背包容量的值初始化为-inf,背包容量为0的值初始化为0,这点在《背包九讲》中写得很清楚
最后从t往0扫dp的结果,存在>=0的值就是答案,背包容量i对应的剩余时间是 t - i
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 10005;
int f[N];
int c[2];
int main(){
int t;
while(~scanf("%d%d%d", &c[0], &c[1], &t)){
memset(f, -0x3f, sizeof(f));
f[0] = 0;
int ans = 0, time = 0;
for(int i = 0; i <= 1; i++){
for(int j = c[i]; j <= t; j++){
f[j] = max(f[j], f[j - c[i]] + 1);
}
}
for(int i = t; i >= 0; i--){
if(f[i] >= 0){
ans = f[i];
time = t - i;
break;
}
}
printf("%d", ans);
if(time) printf(" %d", time);
printf("\n");
}
return 0;
}
Coin Change | UVA 674
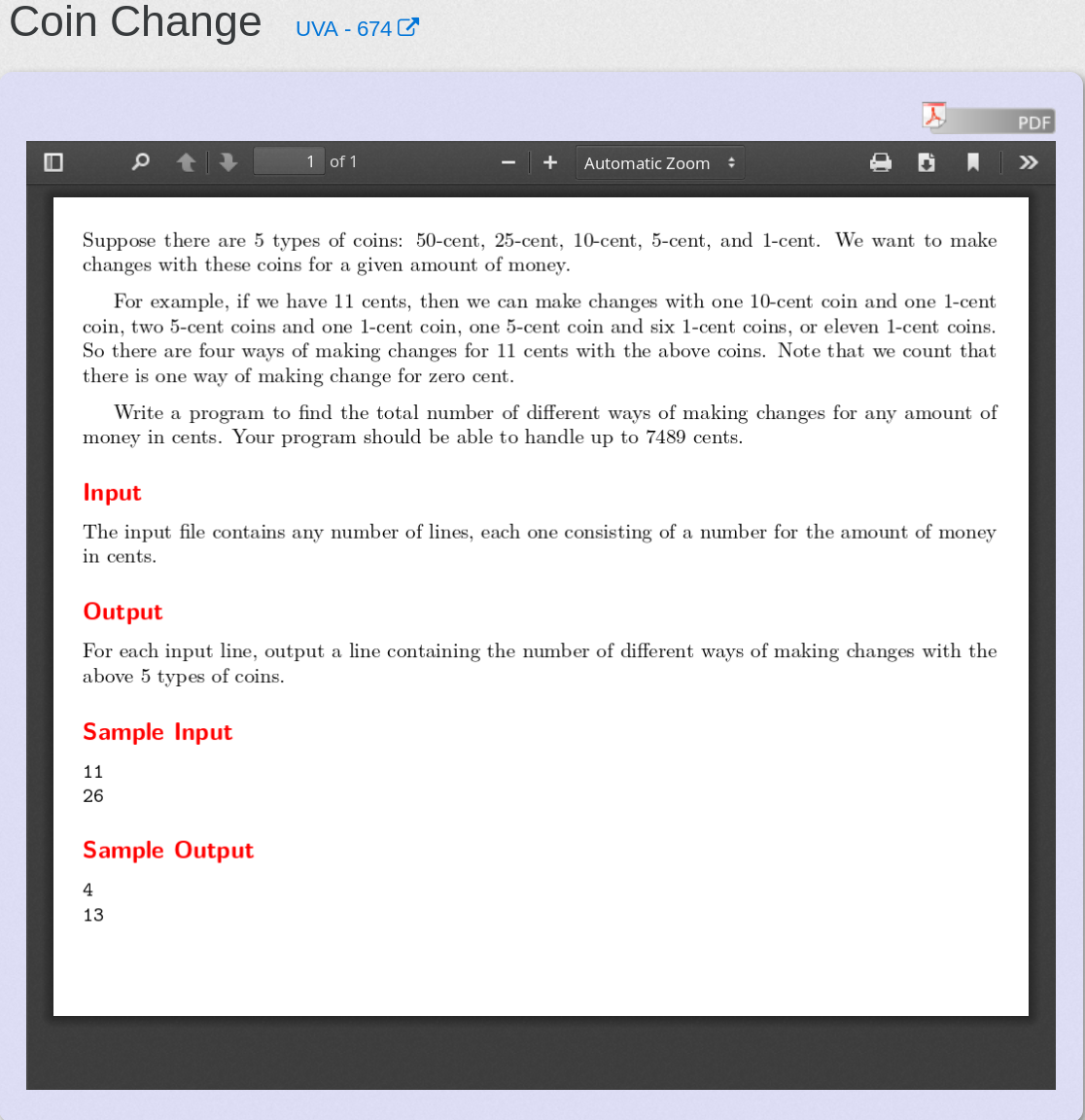 题目大意
题目大意
给定无限的50分,25分,10分,5分,1分的硬币,问其组合成某个数值的钱有多少种可能
思路
目测是 完全背包问题,并且题目给了个提示 “认为组成0有1种可能”, 所以可以列出状态方程 f[i][j] = f[i - 1][j] + f[i][j - c[i]]
其中i是前i种硬币,j是组成数值为j的钱
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 7490;
int f[N];
int c[] = {1, 5, 10, 25, 50};
int main(){
int n = 5, m = N;
memset(f, 0, sizeof(f));
f[0] = 1;
for(int i = 0; i < n; i++){
for(int j = c[i]; j < m; j++){
if(f[j - c[i]] >= 0){
f[j] += f[j - c[i]];
}
}
}
int in;
while(~scanf("%d", &in)){
printf("%d\n", f[in]);
}
return 0;
}
Bottles | CodeForces 730J
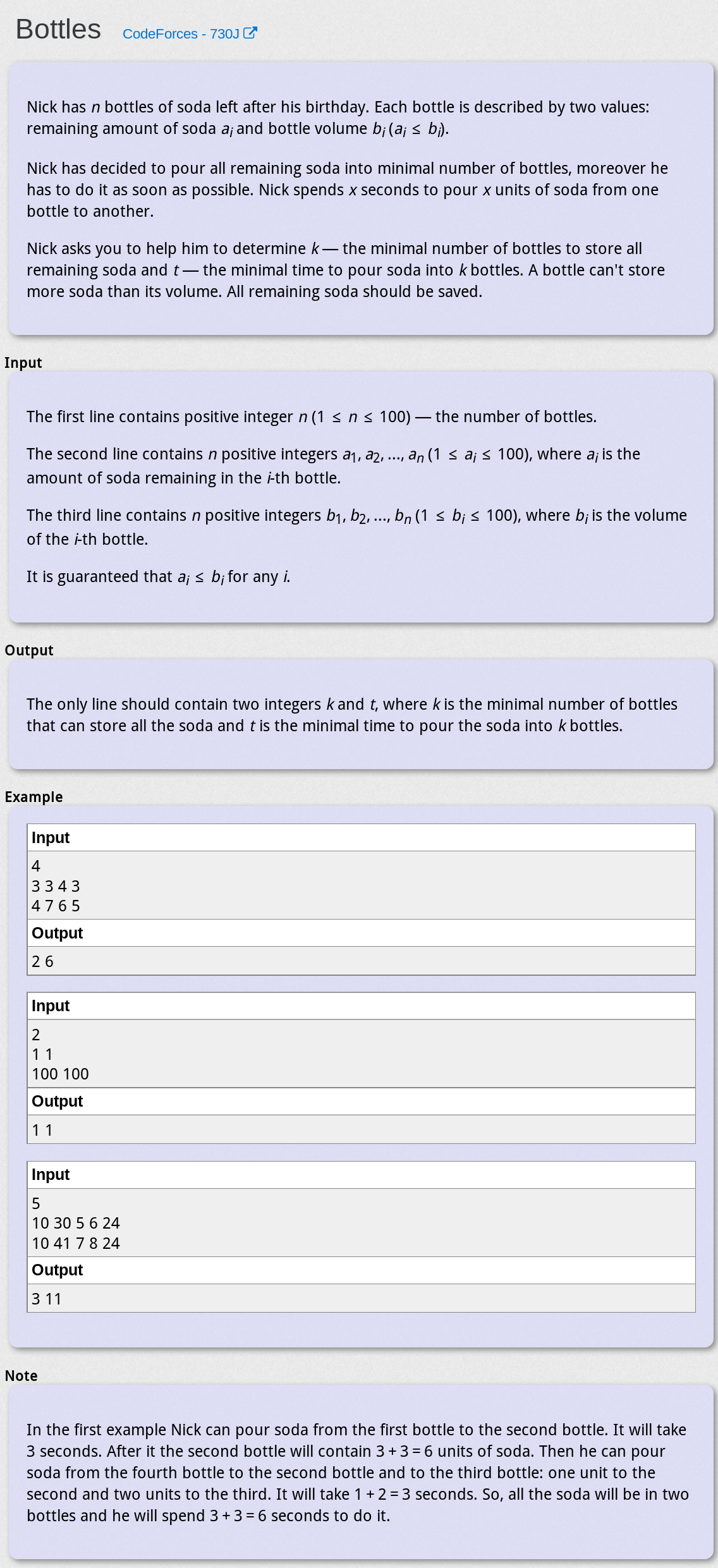 题目大意
题目大意
给定n个装有苏打水的瓶子,第i个瓶子的容量为bi L,装有ai L苏打水,现在要把全部苏打水倒入尽可能少的瓶子里,以便撤走几个瓶子,求满足要求的剩余瓶子最少数量,以及在此情况下转移苏打水最少的量
思路
要求瓶子的最少数量,而这些瓶子肯定要能装下至少∑a[i]的水,所以可以考虑把瓶子容量作为c[i]进行DP,转化为 01背包问题 进行求解
在这个问题中,主要价值就应该是瓶子的数量,而次要价值应该是所装苏打水的量,主要价值相同时,更新次要价值大者,因为要想转移苏打水最少,需要原来选择的瓶子中所装苏打水最多,毕竟∑a[i]是个定量
另外,因为dp的是瓶子容量,所以要求的是装满时的最优解,本题中因为主要价值是瓶子的数量,并且要求数量最少,故将瓶子容量初始化为inf,DP完后从f[∑a[i]]开始正着扫,扫值最小且次要价值最大者
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 102;
const int INF = 0x3f3f3f3f;
typedef long long ll;
int f[N*N], g[N*N];
int b[N], c[N];
int main(){
int n;
while(~scanf("%d", &n)){
int sum = 0, ans_nums = INF, ans_liter;
for(int i = 0; i < n; i++){
scanf("%d", &b[i]);
sum += b[i];
}
for(int i = 0; i < n; i++){
scanf("%d", &c[i]);
}
memset(f, 0x3f, sizeof(f));
memset(g, 0, sizeof(g));
f[0] = 0;
for(int i = 0; i < n; i++){
for(int j = N*N - 1; j >= c[i]; j--){
if(f[j] > f[j - c[i]] + 1){
f[j] = f[j - c[i]] + 1;
g[j] = g[j - c[i]] + b[i];
}else if(f[j] == f[j - c[i]] + 1){
g[j] = max(g[j], g[j - c[i]] + b[i]);
}
}
}
for(int i = sum; i < N*N; i++){
if(f[i] < ans_nums){
ans_nums = f[i];
ans_liter = sum - g[i];
}else if(f[i] == ans_nums && ans_liter > sum - g[i]){
ans_liter = sum - g[i];
}
}
printf("%d %d\n", ans_nums, ans_liter);
}
return 0;
}
Cash Machine | POJ 1276
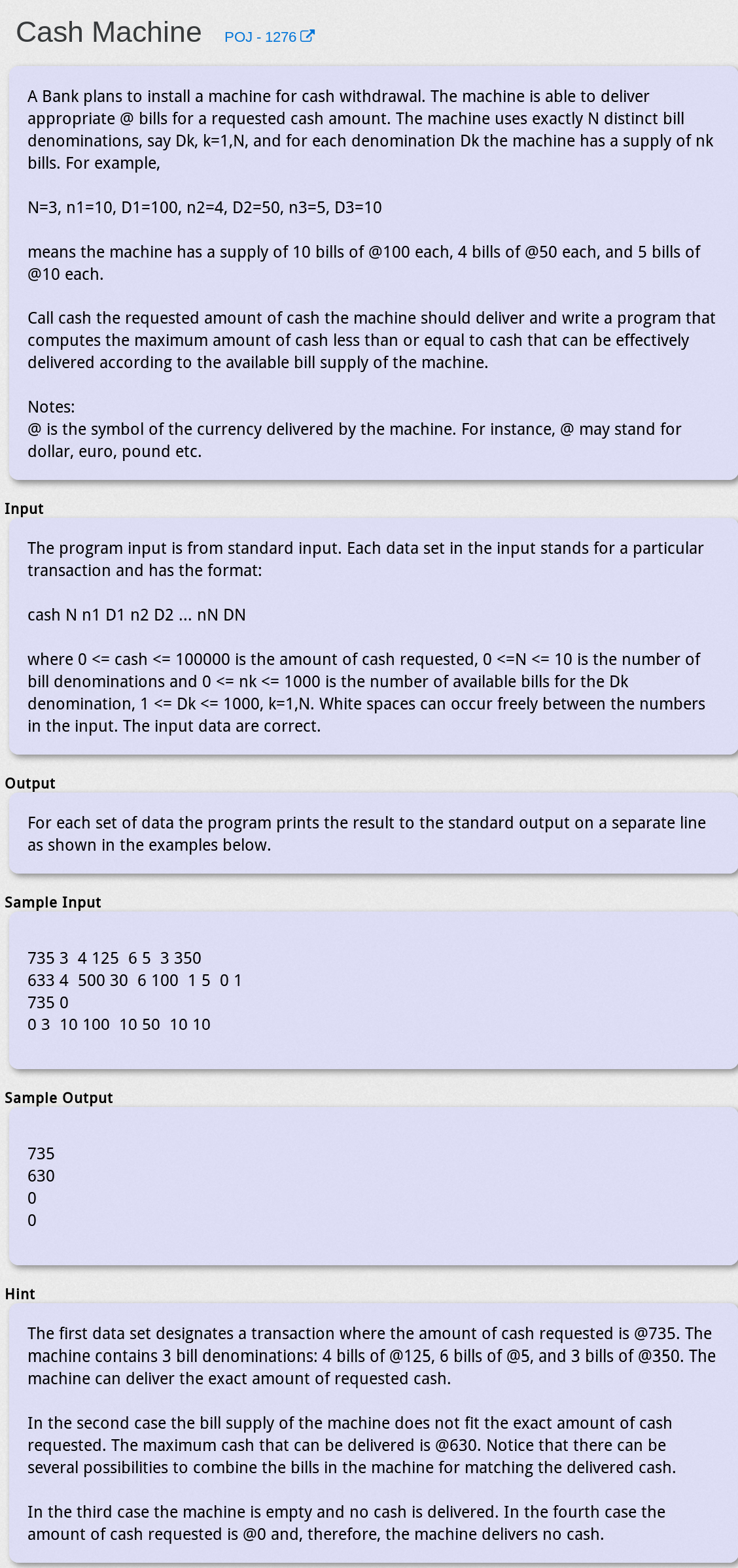 题目大意
题目大意
给定N种有限量的钱币面额,其中面额为Di的钱币有ni张,问能用这些钱币组合出不超过cash的最大面额是多少
思路
典型 多重背包问题, 用二进制思想将一件物品拆成多件物品,然后转化成01背包问题求解
《背包九讲》中有详细的说明,故不赘述
另外《背包九讲》那个拆成二进制表示的伪代码好像不对……
#include <cstdio>
#include <cmath>
#include <cstring>
#include <iostream>
using namespace std;
const int N = 100005;
int c[N], f[N];
int main(){
int v, n;
while(~scanf("%d%d", &v, &n)){
memset(f, 0, sizeof(f));
int cend = 0;
for(int i = 0; i < n; i++){
int nk, dk;
scanf("%d%d", &nk, &dk);
if(nk == 0) continue;
int j = 1, sum = 0;
while(true){
c[cend++] = dk*j;
sum += j;
j <<= 1;
if(nk - sum - j < 0) break; //和《背包九讲》的公式不同之处就在这里
}
c[cend++] = dk*(nk - sum);
}
for(int i = 0; i < cend; i++){
for(int j = v; j >= c[i]; j--){
f[j] = max(f[j], f[j - c[i]] + c[i]);
}
}
printf("%d\n", f[v]);
}
return 0;
}


