拓扑排序
更新(20180727)
首先打脸,更新了更新了
修改一下以前写的比较渣的代码
改完了,发现怎么4个月前写的代码这么辣鸡…
前言
做了些题目后发现呢,这个拓扑排序用于解决有先后次序的问题,而且特别实用!即使是在日常生活也感觉它特别的实用!
另外关于拓扑排序的计数问题,有时间啃完 + 啃得下就再发新的文
- 拓扑排序 —— 百度百科
https://baike.baidu.com/item/%E6%8B%93%E6%89%91%E6%8E%92%E5%BA%8F - 拓扑排序
http://blog.csdn.net/qq_35644234/article/details/60578189
题
不会做的题
- Frame Stacking | POJ 1128
- Permutation | HDU 4917
Genealogical tree | POJ-2367
 题目大意
题目大意
有N个人,他们知道他们的后代有谁,以及他们各自的编号,求他们从长辈到晚辈顺序的编号序列
思路
模板题来着的
//[POJ - 2367]
#include <cstdio>
#include <cstring>
#include <queue>
#include <vector>
using namespace std;
const int N = 1e4 + 15;
struct edge{
int v, val, next;
edge(int pv, int pval, int pnext): v(pv), val(pval), next(pnext) {}
edge() {}
};
edge e[N]; //e[i].next记录e[i]的相邻边为第几条边
int head[N]; //head[i]记录以i为出发点的最后一条边是第几条边
int tot; //边的总数
int idg[N]; //入度
queue<int> que;
vector<int> ans;
void addedge(int u, int v, int val){
e[tot] = edge(v, val, head[u]);
head[u] = tot++;
idg[v]++;
}
//tot : 函数完成时代表总共几条边,函数执行时代表是第几条边
//e[tot].next : 记录上一次从from出发的边是第几条边,即e[tot]的邻近边,因此可用此遍历从from出发的所有边,到-1时遍历完成
//head[u] = tot : 更新这次从from出发的边是第tot边
void init(){
memset(head, -1, sizeof(head));
memset(idg, 0, sizeof(idg));
while(!que.empty()) que.pop();
ans.clear();
tot = 0;
}
void topoSort(int n){
for(int i = 1; i <= n; i++){
if(!idg[i]) que.push(i);
}
while(!que.empty()){
int u = que.front();
que.pop();
ans.push_back(u);
for(int i = head[u]; ~i; i = e[i].next){
int v = e[i].v;
if((--idg[v]) == 0) que.push(v);
}
}
}
int main(){
int n;
while(~scanf("%d", &n)){
init();
for(int i = 1; i <= n; i++){
int v;
while(scanf("%d", &v) && v) addedge(i, v, 0);
}
topoSort(n);
for(int i = 0; i < ans.size(); i++){
printf("%d", ans[i]);
if(i < ans.size() - 1) putchar(' ');
}
}
return 0;
}
Sorting It All Out | POJ 1094
 题目大意
题目大意
给定n个字母之间的m条关系,判断能否确定唯一序列,第i条关系能判断则输出结果,第i条关系后矛盾则输出在第i条关系时矛盾,不能确定唯一则输出不能确定
思路
其实这题我查了一点点的题解,因为比较懵逼如何输出第几条关系,结果题解给出的方法是:每加入一条就进行一次topoSort……有点暴力呀这方法……
矛盾就是图中有环,topoSort结束后仍然有入度不为0的点
不能确定就是在最后一条关系式进行topoSort时,存在某次队列中的元素超过1个的情况
//[POJ-1094]
#include <cstdio>
#include <cstring>
#include <iostream>
#include <queue>
using namespace std;
const int N = 1e5 + 15;
const int inf = 0x3f3f3f3f;
struct edge{
int v, next;
edge(int pv, int pnext): v(pv), next(pnext) {}
edge() {}
};
edge e[N];
int head[N], idg[N], idg_cpy[N];
int tot;
queue<int> que;
void init(){
memset(head, -1, sizeof(head));
memset(idg_cpy, 0, sizeof(idg_cpy));
tot = 0;
}
void addedge(int u, int v){
e[tot] = edge(v, head[u]);
head[u] = tot++;
idg_cpy[v]++;
}
int topoSort(int n, string& ans){
ans.clear();
int flag = 0; //初始为确定顺序状态
int sum = 0;
memcpy(idg, idg_cpy, sizeof(idg_cpy));
for(int i = 0; i < n; i++){
if(!idg[i]) que.push(i);
}
while(!que.empty()){
if(que.size() > 1) flag = 1; //不能确定,某次队列中的元素超过1个
int u = que.front();
que.pop();
sum++;
ans.push_back(u + 'A');
for(int i = head[u]; ~i; i = e[i].next){
int v = e[i].v;
if((--idg[v]) == 0) que.push(v);
}
}
if(sum != n) flag = -1; //有环
return flag;
}
int main(){
int n, m;
while(~scanf("%d%d", &n, &m) && n + m){
init();
string ans;
int s = inf, stat = 1;
for(int i = 1; i <= m; i++){
char str[4];
scanf("%s", str);
//已经确定顺序或矛盾就不用再进行topoSort了,但是要读完
if(stat == -1 || stat == 0) continue;
int u = str[0] - 'A', v = str[2] - 'A';
addedge(u, v);
stat = topoSort(n, ans);
if(stat == 0 || stat == -1) s = i;
}
if(stat == -1) printf("Inconsistency found after %d relations.\n", s);
else if(stat == 1) printf("Sorted sequence cannot be determined.\n");
else printf("Sorted sequence determined after %d relations: %s.\n", s, ans.c_str());
}
return 0;
}
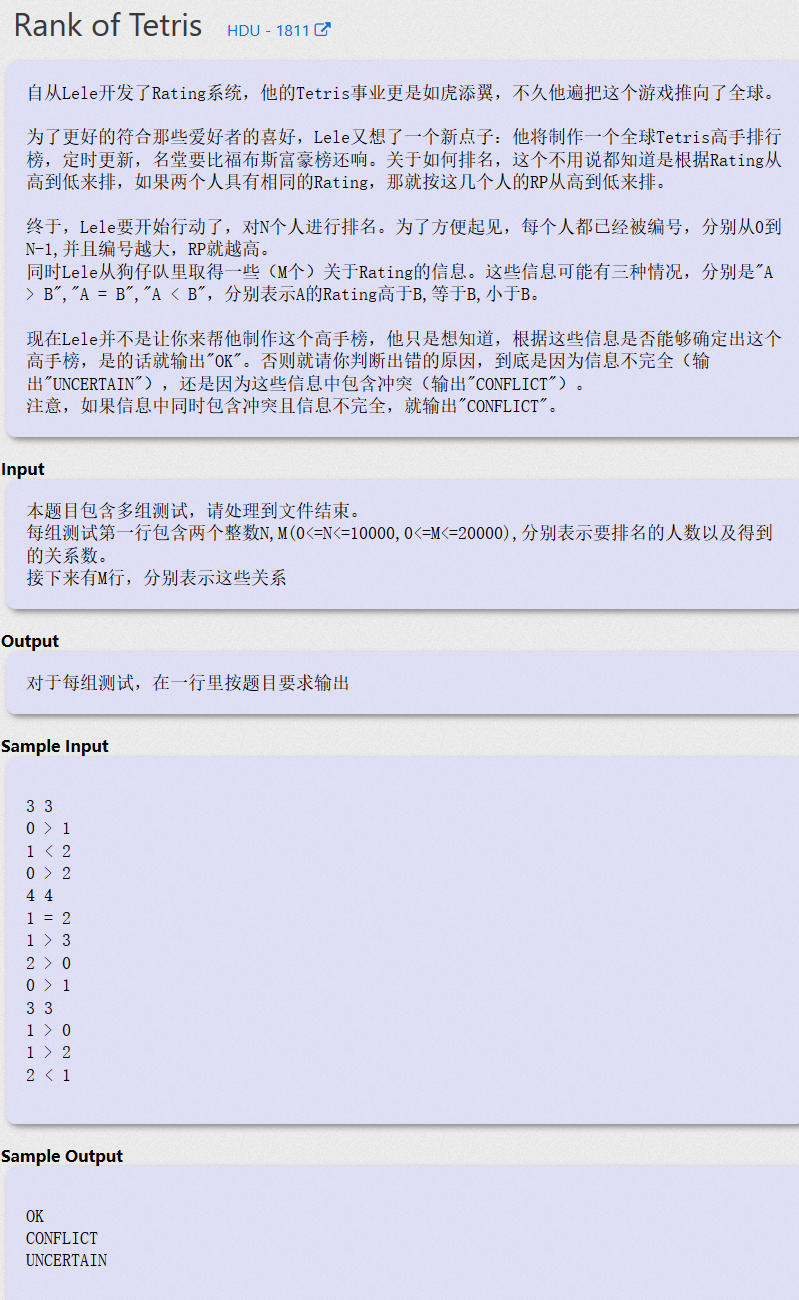
Rank of Tetris | HDU 1811
 题目大意
题目大意
中文的就不解释了(•̀ᴗ•́)و ̑̑
思路
和普通的topoSort相比,最大的区别就是有 = 号,而topoSort本身是给出先后顺序序列,没办法(或者我不知道)来解决 = 号的问题,因此可以引入 并查集 来解决
先将<和>的关系存起来,遇到 = 号就合并,读入完后再加边,然后就像普通的topoSort一样做就行
//[HDU-1811]
#include <cstdio>
#include <cstring>
#include <queue>
using namespace std;
const int N = 2e4 + 15;
struct edge{
int v, next;
edge(int pv, int pnext): v(pv), next(pnext) {}
edge() {}
};
edge e[N];
int head[N], idg[N];
int tot;
int ft[N];
queue<int> que;
int rel[N][2];
void init(int n){
memset(head, -1, sizeof(head));
memset(idg, 0, sizeof(idg));
tot = 0;
for(int i = 0; i < n; i++) ft[i] = i;
}
int find(int x) { return (ft[x] == x ? x : ft[x] = find(ft[x])); }
void merge(int x, int y){
int p = find(x), q = find(y);
if(p != q) ft[q] = p;
}
void addEdge(int u, int v){
e[tot] = edge(v, head[u]);
head[u] = tot++;
idg[v]++;
}
void topoSort(int n){
int flag = 0; //0:OK, 1:UNCERTAIN; -1:CONFLICT
int sum = 0, m = 0;
for(int i = 0; i < n; i++){
if(ft[i] != i) continue; //注意排除掉不为本身的点,因为他们都归到父节点去了
if(!idg[i]) que.push(i);
m++;
}
while(!que.empty()){
if(que.size() > 1) flag = 1;
int u = que.front();
que.pop();
sum++;
for(int i = head[u]; ~i; i = e[i].next){
int v = e[i].v;
if((--idg[v]) == 0) que.push(v);
}
}
if(sum != m) puts("CONFLICT");
else if(flag == 0) puts("OK");
else puts("UNCERTAIN");
}
int main(){
int n, m;
while(~scanf("%d%d", &n, &m)){
init(n);
int t = 0;
for(int i = 0; i < m; i++){
int a, b;
char op;
scanf("%d %c %d", &a, &op, &b);
if(op == '=') merge(a, b); // 合并 =
else{
if(op == '>') swap(a, b);
rel[t][0] = a, rel[t][1] = b; // > 转 <,都存起来
t++;
}
}
for(int i = 0; i < t; i++){
int u = find(rel[i][0]), v = find(rel[i][1]); // 加边是用父节点加
addEdge(u, v);
}
topoSort(n);
}
return 0;
}
-0你电脑炸啦 | SCU 4521
 题目大意
题目大意
照样不解释,懒~
思路
第一次看到这道题还是几个月前,现在看这题就是送分的嘛
有先后次序问题,所以可以topoSort
每次都扫描一个2x2的面积,看看除本身值以外还有哪些值,加边,然后topoSort能完成就OK,完成不了就GG
//[SCU-4521]
#include <cstdio>
#include <cmath>
#include <climits>
#include <cstring>
#include <iostream>
#include <queue>
#include <vector>
using namespace std;
const int N = 2e4 + 15;
struct edge{
int v, next;
edge(int pv, int pnext): v(pv), next(pnext) {}
edge() {}
};
edge e[N];
int head[N];
int tot;
int idg[N];
int G[5][5];
queue<int> que;
const int dx[] = {0, 1, 1, 0}; //本身,本身右方、下方和右下方(不按实际代码顺序)
const int dy[] = {0, 0, 1, 1};
void init(){
memset(head, -1, sizeof(head));
memset(idg, 0, sizeof(idg));
tot = 0;
}
void addEdge(int u, int v){
e[tot] = edge(v, head[u]);
head[u] = tot++;
idg[v]++;
}
bool topoSort(int n){
int sum = 0;
for(int i = 1; i <= n; i++){
if(!idg[i]) que.push(i);
}
while(!que.empty()){
int u = que.front();
que.pop();
sum++;
for(int i = head[u]; ~i; i = e[i].next){
int v = e[i].v;
if((--idg[v]) == 0){
que.push(v);
}
}
}
return sum == n;
}
int main(){
int t;
scanf("%d", &t);
while(t--){
init();
for(int i = 1; i <= 4; i++){
for(int j = 1; j <= 4; j++){
scanf("%d", &G[i][j]);
}
}
for(int i = 1; i <= 3; i++){
for(int j = 1; j <= 3; j++){
int now = (i - 1) * 3 + j; //本来这块地方应该出现的值
for(int k = 0; k < 4; k++){
if(G[i + dx[k]][j + dy[k]] != now){ //有别的窗口堆叠在上面,即出现先后次序
addEdge(now, G[i + dx[k]][j + dy[k]]);
}
}
}
}
printf("%s\n", topoSort(9) ? "Lucky dog!" : "BOOM!");
}
return 0;
}


