刷题记（连通分量 I） —— 2018.3.25

强连通分量，弱连通分量，双连通分量

Update - 2019/04/01

更新了一年前写的很那啥的代码
更新一些疑难点

前言

这一周真的是感受到人与人之间的差距了……作为一名渣渣花了将近一个星期来理解这三种问题的算法……而且弱连通分量还是不算的，因为弱连通分量可以用并查集解决，也可以在DFS的时候顺便hash。
不光如此，到现在我才能理解师兄的那句话“ACM的题目具有欺骗性”
ACM讲到底就是个智力游戏，要有思维力，还要在极其有限时间内（两年，三年，四年）理解非常多的算法
其实我也不知道我能在这条路上走多久哈哈哈

强连通分量
强连通分量
https://www.oyohyee.com/post/Algorithm/Strongly_connected_components
POJ 2186 —— Popular Cows 题解
https://blog.csdn.net/chang_mu/article/details/38709047
强连通分量的Tarjan算法
https://www.cnblogs.com/tgycoder/p/5048898.html
http://blog.miskcoo.com/2016/07/tarjan-algorithm-strongly-connected-components
https://comzyh.com/blog/archives/517/
双连通分量 + 割点 + 桥
https://sxkdz.org/algorithm-cut-vertex-bridge-bi-connected-component/
https://blog.csdn.net/fuyukai/article/details/51039788
https://blog.csdn.net/fuyukai/article/details/51303292

一些疑难点

Kosaraju算法中，可以直接用后序在原图上DFS，而不建逆图用逆后序DFS嘛？
这样写HDU和POJ的两道模板题都能过，但是是有问题的！
反例就是一位大佬在知乎上提出来的：
1 -> 2, 2 -> 3, 3 -> 4, 4 -> 1, 1 -> 5
参见链接：https://www.zhihu.com/question/265266923/answer/329700845
Tarjan算法中为什么已访问过的点要写 low[u] = min(low[u], dfn[v]) 而不写 low[u] = min(low[u], dfn[v]) ？
动态规划思想
low[u]用于维护自己及其之下所能回到的最早dfn
st[u]是自己的dfn
==== 分割线（以下的之前的想法） === 这样写HDU和POJ的两道模板题也都能过，而且还没发现什么反例……
但是 low[u] = min(low[u], dfn[v]) ，代表遇到当前栈中已访问的点v，且v的时间戳比目前u节点记录的最早low[u]小，就更新low[u]，从算法理解层面来讲这样写合理
点双连通分量
点双连通分量并不一定形成环，例如在下面的图中：
1 - 2, 2 - 3, 2 - 4, 1 - 5, 1 - 6, 5 - 6
点双连通分量总共是： 1 - 5 - 6 - 1, 1 - 2， 2 - 3, 2 - 4
割顶是：1, 2
强连通分量，边双连通分量
二者其实都是一样的，都是形成环
只不过前者用于有向图，后者用于无向图

Popular Cows - POJ 2186

题目大意
在牛群中，A牛喜欢B牛，B牛喜欢C牛，那么A牛喜欢C牛，即喜欢具有传递性，现在问有多少头牛是大家都喜欢的

思路
这题作为强连通分量 + 缩点的模板题
同一个强连通分量内的牛是互相喜欢的，所以缩点处理，缩点后找到出度为0的牛群的数量
如果这样的牛群只有一个，那么那个牛群的数量就是答案了，如果有多个，那么答案为0，因为至少有两个牛群中的任意一方不喜欢另一方

//Kosaraju算法解决强连通分量问题
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
using namespace std;
typedef long long ll;
const int N = 50000 + 15;

struct edge {
    int v, nxt;
};

struct Graph {
    edge e[N];
    int head[N], tot;

    void init(int n) {
        memset(head, -1, (n + 1) * sizeof(int));
        tot = 0;
    }

    void addEdge(int u, int v) {
        e[tot] = edge{v, head[u]};
        head[u] = tot++;
    }
};

Graph g, gt;
int node[N], ndtot;
int used[N];
int mp[N], out[N], cnt[N];

inline void read(int& x) {
    scanf("%d", &x);
}

void dfs(int u) {
    used[u] = 1;
    for(int i = g.head[u]; ~i; i = g.e[i].nxt){
        int v = g.e[i].v;
        if(used[v] != 1) {
            dfs(v);
        }
    }
    node[++ndtot] = u;            //逆后序入栈
}

void dfs1(int u, int fa){
    used[u] = 2;
    for(int i = gt.head[u]; ~i; i = gt.e[i].nxt){
        int v = gt.e[i].v;
        if(used[v] != 2) {
            dfs1(v, fa);
        };
    }
    mp[u] = fa;                 //缩点
    cnt[fa]++;                  //统计缩点后的数量
}

int main(){
    int n, m;
    while(~scanf("%d%d", &n, &m)){
        g.init(n);
        gt.init(n);
        ndtot = 0;
        for(int i = 1; i <= n; i++) {
            used[i] = cnt[i] = out[i] = 0;
        }

        while(m--){
            int u, v;
            read(u), read(v);
            g.addEdge(u, v);
            gt.addEdge(v, u);
        }


        for(int i = 1; i <= n; i++){
            if(used[i] != 1) {
                dfs(i);
            }
        }

        for(int i = n; i >= 1; i--) {
            if(used[node[i]] != 2) {
                dfs1(node[i], node[i]);
            }
        }

        for(int i = 0; i < g.tot; i++){
            int u = gt.e[i].v, v = g.e[i].v;
            if(mp[u] == mp[v]) {
                continue;   //在同一个连通分量的不统计出度
            }
            out[mp[u]]++;
        }

        int t = 0, ans = 0;
        for(int i = 1; i <= n; i++){
            if(mp[i] != i)  continue;
            if(out[i] == 0){
                t++;                    //出度为0的点的数量
                ans = cnt[i];
            }
        }
        if(t == 1){
            printf("%d\n", ans);
        }else{
            printf("0\n");
        }
    }
    return 0;
}

//Tarjan算法解决强连通分量问题
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#include <stack>
using namespace std;
typedef long long ll;
const int N = 50000 + 15;

struct edge {
    int u, v, nxt;
};

edge e[N];
int head[N], tot;
bool instk[N];
int mp[N], out[N], cnt[N];
int low[N], st[N], dfn;
stack<int> stk;

inline void read(int& x) {
    scanf("%d", &x);
}

inline void addEdge(int u, int v) {
    e[tot] = edge{u, v, head[u]};
    head[u] = tot++;
}

void Tarjan(int u) {
    low[u] = st[u] = ++dfn;
    stk.push(u);
    instk[u] = true;
    for(int i = head[u]; ~i; i = e[i].nxt) {
        int v = e[i].v;
        if(st[v] == 0) {
            Tarjan(v);
            low[u] = min(low[u], low[v]);
        } else if(instk[v]){
            low[u] = min(low[u], st[v]);
        }
    }
    if(low[u] == st[u]) {
        while(true) {
            int v = stk.top();
            stk.pop();
            instk[v] = false;
            mp[v] = u;
            cnt[u]++;
            if(u == v) {
                break;
            }
        }
    }
}

int main(){
    int n, m;
    while(~scanf("%d%d", &n, &m)){
        memset(head, -1, sizeof(head));
        dfn = 0;
        for(int i = 1; i <= n; i++) {
            cnt[i] = out[i] = st[i] = 0;
        }

        while(m--){
            int u, v;
            read(u), read(v);
            addEdge(u, v);
        }

        for(int i = 1; i <= n; i++){
            if(st[i] == 0) {
                Tarjan(i);
            }
        }

        for(int i = 0; i < tot; i++){
            int u = e[i].u, v = e[i].v;
            if(mp[u] == mp[v]) {
                continue;   //在同一个连通分量的不统计出度
            }
            out[mp[u]]++;
        }

        int t = 0, ans = 0;
        for(int i = 1; i <= n; i++){
            if(mp[i] != i)  continue;
            if(out[i] == 0){
                t++;                    //出度为0的点的数量
                ans = cnt[i];
            }
        }
        printf("%d\n", t == 1 ? ans : 0);
    }
    return 0;
}

Data Center Maintenance - CodeForces-950E

题目大意
数据中心有n台服务器，他们的每个客户的数据放在两个不同的服务器上，假设一天有h小时。现在数据中心的服务器在0至h - 1时间内需要各自维护一个小时，给定每台服务器维护的时刻表，这个时刻表保证每名客户能在任意时刻访问到自己的数据，现在问将其中至少多少台服务器的维护时刻推后一个小时（其中h - 1时刻推后到0时刻），能使得每名客户都还能在任意时刻访问到自己的数据

思路
“ACM的题目具有欺骗性”，这题乍一看，和强连通分量半毛钱关系都没有呀！
都是不妨想想，如果放置同一名客户的两台服务器维护时刻相差1,那么其中维护时刻小的那台向后推移，另一台就得跟着向后推移，由此可以构成一个有向图，其中被指向的点是受起点推移而推移的点，在一个圈内的点，一个推移，个个推移，所以可以求强连通分量后缩点，找到出度为0并且数量最小的点，就是答案了

#include <bits/stdc++.h>
using namespace std;
const int N = 200000 + 5;
const int inf = 0x3f3f3f3f;

struct edge {
    int v, nxt;
};
edge e[N];
int head[N], tot;

int mp[N], cnt[N], st[N], low[N], out[N], val[N];
int dfn;
bool instk[N];
stack<int> stk;

inline void read(int& x) {
    scanf("%d", &x);
}

inline void addEdge(int u, int v) {
    e[tot] = edge{v, head[u]};
    head[u] = tot++;
}

void Tarjan(int u) {
    low[u] = st[u] = ++dfn;
    stk.push(u);
    instk[u] = true;
    for(int i = head[u]; ~i; i = e[i].nxt) {
        int v = e[i].v;
        if(st[v] == 0) {
            Tarjan(v);
            low[u] = min(low[u], low[v]);
        } else if(instk[v]){
            low[u] = min(low[u], st[v]);
        }
    }
    if(low[u] == st[u]) {
        while(true) {
            int v = stk.top();
            stk.pop();
            instk[v] = false;
            mp[v] = u;
            cnt[u]++;
            if(u == v) {
                break;
            }
        }
    }
}

int main() {
    int n, m, h;
    read(n), read(m), read(h);

    tot = dfn = 0;
    for(int i = 1; i <= n; i++) {
        head[i] = -1;
        cnt[i] = st[i] = out[i] = 0;
    }

    int ans_cnt = inf, ans = 0;
    for(int i = 1; i <= n; i++) {
        read(val[i]);
    }
    for(int i = 1; i <= m; i++) {
        int u, v;
        read(u), read(v);
        if(val[u] == (val[v] + 1) % h) {
            addEdge(v, u);
        }
        if(val[v] == (val[u] + 1) % h) {
            addEdge(u, v);
        }
    }
    for(int i = 1; i <= n; i++) {
        if(st[i] == 0) {
            Tarjan(i);
        }
    }

    for(int u = 1; u <= n; u++) {
        for(int i = head[u]; ~i; i = e[i].nxt) {
            int v = e[i].v;
            if(mp[u] != mp[v]) {
                out[mp[u]]++;
            }
        }
    }

    for(int i = 1; i <= n; i++) {
        if(mp[i] != i)  continue;
        if(out[i] == 0 && ans_cnt > cnt[i]) {
            ans_cnt = cnt[i];
            ans = i;
        }
    }

    printf("%d\n", ans_cnt);
    for(int i = 1; i <= n; i++) {
        if(mp[i] == ans) {
            printf("%d ", i);
        }
    }
    printf("\n");

    return 0;
}

Mr. Kitayuta’s Technology - CodeForces-505D

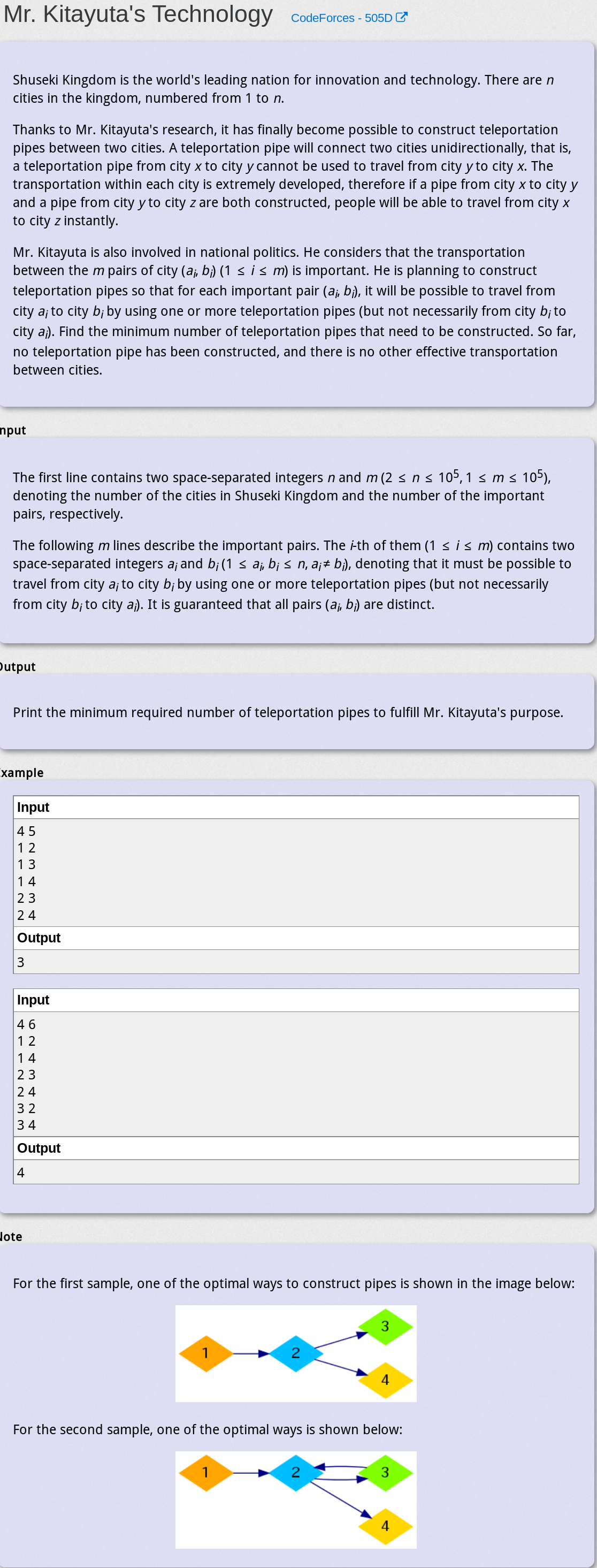
题目大意
给定一个图，求最少用几条边重新架构其中的弱连通分量而保证原图各点的连通性依旧存在

思路
翻了一下题解……自己宛若智障……
如果原来那个弱连通分量里有强连通分量，那就干脆把一整个图改为强联通图，否则就改成树，对应的答案为（点数）和（点数 - 1），再求和就行了

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 15;
const int inf = 0x3f3f3f3f;

struct edge {
    int v, nxt;
};
edge e[N];
int head[N], tot;

int mp[N], cnt[N], st[N], low[N], val[N];
int dfn;
bool instk[N];
stack<int> stk;

int ft[N], ftcnt[N];
bool isCircle[N];

int find(int x) {
    return ft[x] == x ? x : ft[x] = find(ft[x]);
}
void merge(int x, int y) {
    int p = find(x), q = find(y);
    if(p != q) {
        ft[q] = p;
    }
}

inline void read(int& x) {
    scanf("%d", &x);
}

inline void addEdge(int u, int v) {
    e[tot] = edge{v, head[u]};
    head[u] = tot++;
}

void Tarjan(int u) {
    low[u] = st[u] = ++dfn;
    stk.push(u);
    instk[u] = true;
    for(int i = head[u]; ~i; i = e[i].nxt) {
        int v = e[i].v;
        merge(u, v);
        if(st[v] == 0) {
            Tarjan(v);
            low[u] = min(low[u], low[v]);
        } else if(instk[v]){
            low[u] = min(low[u], st[v]);
        }
    }
    if(low[u] == st[u]) {
        while(true) {
            int v = stk.top();
            stk.pop();
            instk[v] = false;
            mp[v] = u;
            cnt[u]++;
            if(u == v) {
                break;
            }
        }
    }
}

int main() {
    int n, m;
    while(~scanf("%d%d", &n, &m)) {
        tot = dfn = 0;
        for(int i = 1; i <= n; i++) {
            head[i] = -1;
            st[i] = cnt[i] = ftcnt[i] = 0;
            ft[i] = i;
            isCircle[i] = false;
        }

        int ans = 0;
        while(m--) {
            int u, v;
            read(u), read(v);
            addEdge(u, v);
        }
        for(int i = 1; i <= n; i++) {
            if(st[i] == 0) {
                Tarjan(i);
            }
        }
        for(int i = 1; i <= n; i++) {
            int ift = find(i);
            if(mp[i] != i)      continue;
            if(cnt[i] != 1) {
                isCircle[ift] = true;
                ftcnt[ift] += cnt[i] - 1;
            }
            ftcnt[ift]++;
        }
        for(int i = 1; i <= n; i++) {
            int ift = find(i);
            if(ift != i)  continue;
            ans += ftcnt[i] - (isCircle[i] == 0);
        }
        printf("%d\n", ans);
    }
    return 0;
}

SPF - POJ 1523

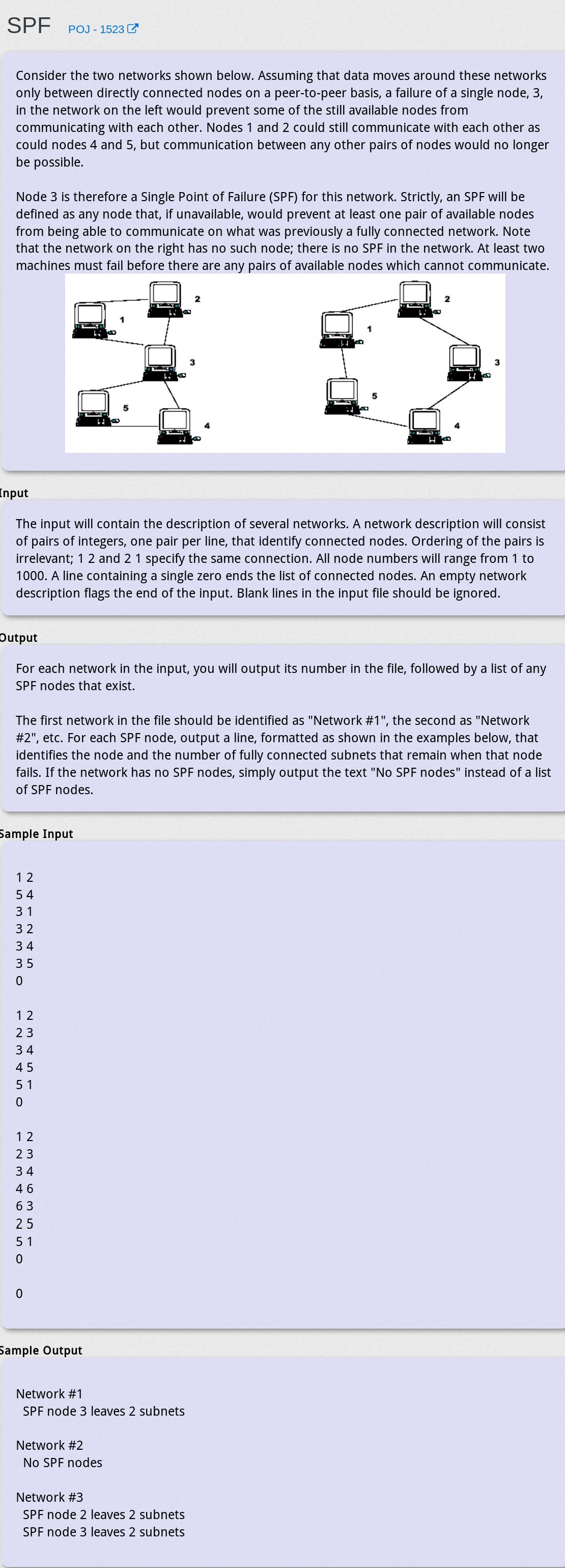题目大意
求连通图中的割点以及去掉该割点后有多少个连通分量

思路
求割点是没什么好说的，问题是求去掉割点后有多少个连通分量
有点儿考算法理解程度……回溯时 low[v] >= dfn[u]，不仅代表u是割点，也代表v这棵子树是u的一个孩子，那么如果u是根节点，去掉后连通分量数就是u的孩子数（显而易见），如果u不是根节点，去掉后连通分量数则为（u的孩子数 + 1），这个‘1’是u的父节点以上那一块

#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 1000 + 15;
const int INF = 0x3f3f3f3f;

struct edge {
    int v, nxt;
};
edge e[N * N * 2];
int head[N], tot;

int st[N], low[N], cnt[N], nodeChildNums[N];
int dfn;
bool isCut[N], isRoot[N], used[N];

inline void read(int& x) {
    scanf("%d", &x);
}

inline void addEdge(int u, int v) {
    e[tot] = edge{v, head[u]};
    head[u] = tot++;
}

void Tarjan(int u, int pre) {
    st[u] = low[u] = ++dfn;
    int childNums = 0;
    for(int i = head[u]; ~i; i = e[i].nxt) {
        int v = e[i].v;
        if(st[v] == 0) {
            childNums++;
            Tarjan(v, u);
            low[u] = min(low[u], low[v]);
            if(low[v] >= st[u]) {
                nodeChildNums[u]++;
                isCut[u] = true;
            }
        } else if(v != pre && st[v] < st[u]) {
            low[u] = min(low[u], st[v]);
        }
    }
    if(pre == -1 && childNums == 1) {
        isCut[u] = false;
    }
}

int main() {
    int u, v, csn = 1;
    while(true) {
        tot = dfn = 0;
        for(int i = 1; i < N; i++) {
            head[i] = -1;
            st[i] = nodeChildNums[i] = 0;
            isRoot[i] = isCut[i] = false;
        }

        v = -1;
        while(scanf("%d", &u) && u) {
            scanf("%d", &v);
            addEdge(u, v);
            addEdge(v, u);
        }
        if(v == -1) {
            break;
        }

        if(csn != 1) {
            puts("");
        }
        printf("Network #%d\n", csn++);
        for(int i = 1; i < N; i++) {
            if(st[i] == 0) {
                isRoot[i] = true;
                Tarjan(i, -1);
            }
        }

        bool flag = true;
        for(int i = 1; i <= 1000; i++) {
            if(isCut[i]) {
                flag = false;
                printf("  SPF node %d leaves %d subnets\n", i, nodeChildNums[i] + (isRoot[i] == false));
            }
        }
        if(flag) {
            puts("  No SPF nodes");
        }
    }
    return 0;
}

Mining Your Own Business - UVALive - 5135

题目大意
假设一开始的一个图是不与外界连通的，在这个图中至少加入多少条连接外界的边，能使得这个图去掉任意点后的其余点通过边仍能和外界连通

思路
首先，可以肯定不能加在割顶，因为把割顶去掉会直接导致割顶连接的两个点双连通分量不能连接外界
第二，一个点双连通中如果有一个割顶，那么这个双连通分量中加一条边就可以了，不加在割顶上
第三，如果一个点双连通中有多个割顶，那么这个双连通中也不需要加边，因为有多个割顶必定连接多个点双连通分量，任何一个点挂掉，必定仍然和某个双连通相连，而一个割顶的点双连通中又含有一条与外界相连的边
特殊的，如果一个图中没有割顶，那么选择任意位置的两个点加边即可
最后一波乘法原理算出有多少种可能性

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#include <stack>
using namespace std;
typedef long long ll;
const int N = 1e5 + 15;
const int inf = 0x3f3f3f3f;

struct edge {
    int u, v, nxt;
};
edge e[N];
int head[N], tot;

int st[N], low[N], cnt[N];
int dfn;
stack<int> stk;

bool isCut[N];
int bccCnt[N], bccCut[N];
int bccNo;

inline void read(int& x) {
    scanf("%d", &x);
}

inline void addEdge(int u, int v) {
    e[tot] = edge{u, v, head[u]};
    head[u] = tot++;
}

void Tarjan(int u, int pre) {
    st[u] = low[u] = ++dfn;
    int childNums = 0;
    for(int i = head[u]; ~i; i = e[i].nxt) {
        int v = e[i].v;
        if(v == pre) {
            continue;
        }

        if(st[v] == 0) {
            stk.emplace(i);
            Tarjan(v, u);
            childNums++;
            low[u] = min(low[u], low[v]);
            if(low[v] >= st[u]) {
                isCut[u] = true;
                bccNo++;

                while(true) {
                    int ecur = stk.top();
                    stk.pop();
                    bccCnt[bccNo]++;      //所属双连通分量点个数++
                    if(isCut[e[ecur].v]) {
                        bccCut[bccNo]++;    //是割点，则所属双连通分量割点数++
                    }
                    if(ecur == i) {
                        break;
                    }
                }
                bccCut[bccNo]++;          //还要算上u
                bccCnt[bccNo]++;
            }
        } else if(v != pre && st[v] < st[u]) {
            low[u] = min(low[u], st[v]);
        }
    }
    if(childNums == 1 && pre == -1) {
        isCut[u] = false;
        bccCut[bccNo]--;                  //不是割点则对应双连通分量割点数--，根节点必定在最后才计算双连通分量，因为回溯嘛
    }
}

int main() {
    int m, csn = 1;
    while(~scanf("%d", &m) && m) {
        dfn = tot = bccNo = 0;
        for(int i = 1; i < N; i++) {
            head[i] = -1;
            st[i] = bccCnt[i] = bccCut[i] = 0;
            isCut[i] = false;
        }

        int upper = 0;
        while(m--) {
            int u, v;
            read(u), read(v);
            addEdge(u, v);
            addEdge(v, u);
            upper = max(upper, max(u, v));
        }

        ll t = 0, ans = 1;
        for(int i = 1; i <= upper; i++) {
            if(st[i]) {
                continue;
            }

            bccNo = 0;
            memset(bccCnt, 0, sizeof(bccCnt));
            memset(bccCut, 0, sizeof(bccCut));
            Tarjan(i, -1);
            if(bccNo == 1) {
                t += 2;
                ans = ans * (ll)bccCnt[1] * (bccCnt[1] - 1) / 2;
            } else {
                for(int i = 1; i <= bccNo; i++) {
                    if(bccCut[i] > 1) {
                        continue;
                    }
                    t++;
                    ans = ans * (ll)(bccCnt[i] - 1);
                }
            }
        }
        printf("Case %d: %lld %lld\n", csn++, t, ans);
    }

    return 0;
}

Road Construction - POJ-3352

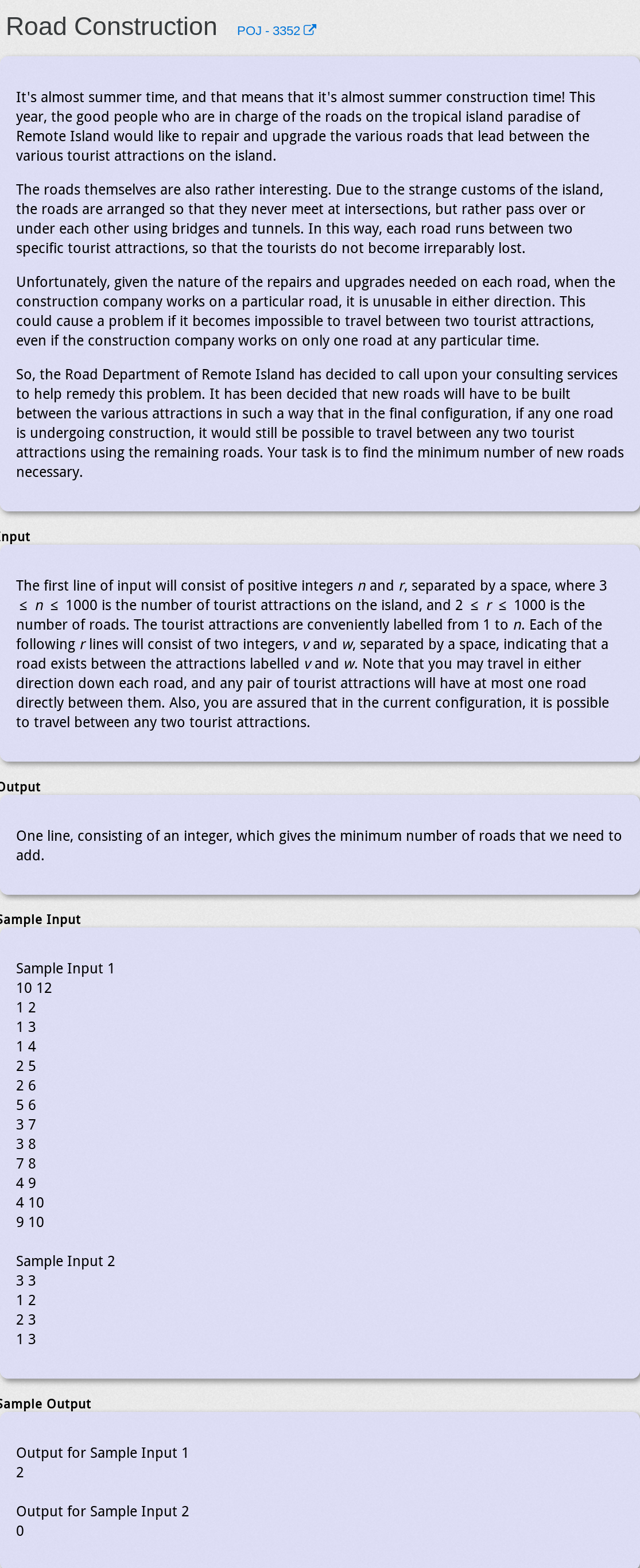
题目大意
给定一个图，问加入几条边后能使整个图是边双连通图

思路
首先原有双连通分量缩点，缩完后找度数为1的点（也就是树的叶子或者只有一个孩子的根），每两个接一条边就行，如果是奇数的话，只好任选一个叶子加一条边，所以答案是（度数为1的点的个数 + 1）/2

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#include <stack>
using namespace std;
typedef long long ll;
const int N = 1000 + 15;

struct edge {
    int u, v, nxt;
};
edge e[N << 1];
int head[N], tot;

int st[N], low[N], idg[N], mp[N];
int dfn;
stack<int> stk;

inline void read(int& x) {
    scanf("%d", &x);
}

inline void addEdge(int u, int v) {
    e[tot] = edge{u, v, head[u]};
    head[u] = tot++;
}

void Tarjan(int u, int pre) {
    low[u] = st[u] = ++dfn;
    stk.push(u);
    for(int i = head[u]; ~i; i = e[i].nxt) {
        int v = e[i].v;
        if(st[v] == 0) {
            Tarjan(v, u);
            low[u] = min(low[u], low[v]);
        } else if(v != pre){
            low[u] = min(low[u], st[v]);
        }
    }
    if(low[u] == st[u]) {
        while(true) {
            int v = stk.top();
            stk.pop();
            mp[v] = u;
            if(u == v) {
                break;
            }
        }
    }
}

int main() {
    int n, m;
    read(n), read(m);

    dfn = tot = 0;
    for(int i = 1; i <= n; i++) {
        st[i] = idg[i] = 0;
        head[i] = -1;
    }

    while(m--) {
        int u, v;
        read(u), read(v);
        addEdge(u, v);
        addEdge(v, u);
    }
    for(int i = 1; i <= n; i++) {
        if(st[i] == 0) {
            Tarjan(i, -1);
        }
    }
    for(int u = 1; u <= n; u++) {
        for(int i = head[u]; ~i; i = e[i].nxt) {
            int v = e[i].v;
            if(mp[v] != mp[u]) {
                idg[mp[v]]++;
            }
        }
    }

    int ans = 0;
    for(int i = 1; i <= n; i++) {
        if(mp[i] != i)  continue;
        if(idg[i] == 1)    ans++;
    }
    printf("%d\n", (ans + 1) >> 1);

    return 0;
}