反素数 和 Emirp



前言

昨天竟然有同学说我打广告！程序猿的事，怎么能叫广告呢[手动滑稽]
反素数有两种，一种找不到英文名，下面的博文具体阐述了那种反素数，另一种是指把一个素数颠倒过来是一个与原数不同的素数，叫做emirp
反素数的题目，简单的就是模板了，难的做不动，会涉及到各类知识，比如排列组合之类的……所以这篇文中都是模板来着的

  1. 反素数 https://blog.csdn.net/ACdreamers/article/details/25049767

不会做的题目

  1. 小明系列故事——未知剩余系 - HDU - 4542
    http://acm.hdu.edu.cn/showproblem.php?pid=4542
  2. Factors - UVALive - 6396
    https://icpcarchive.ecs.baylor.edu/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=4407

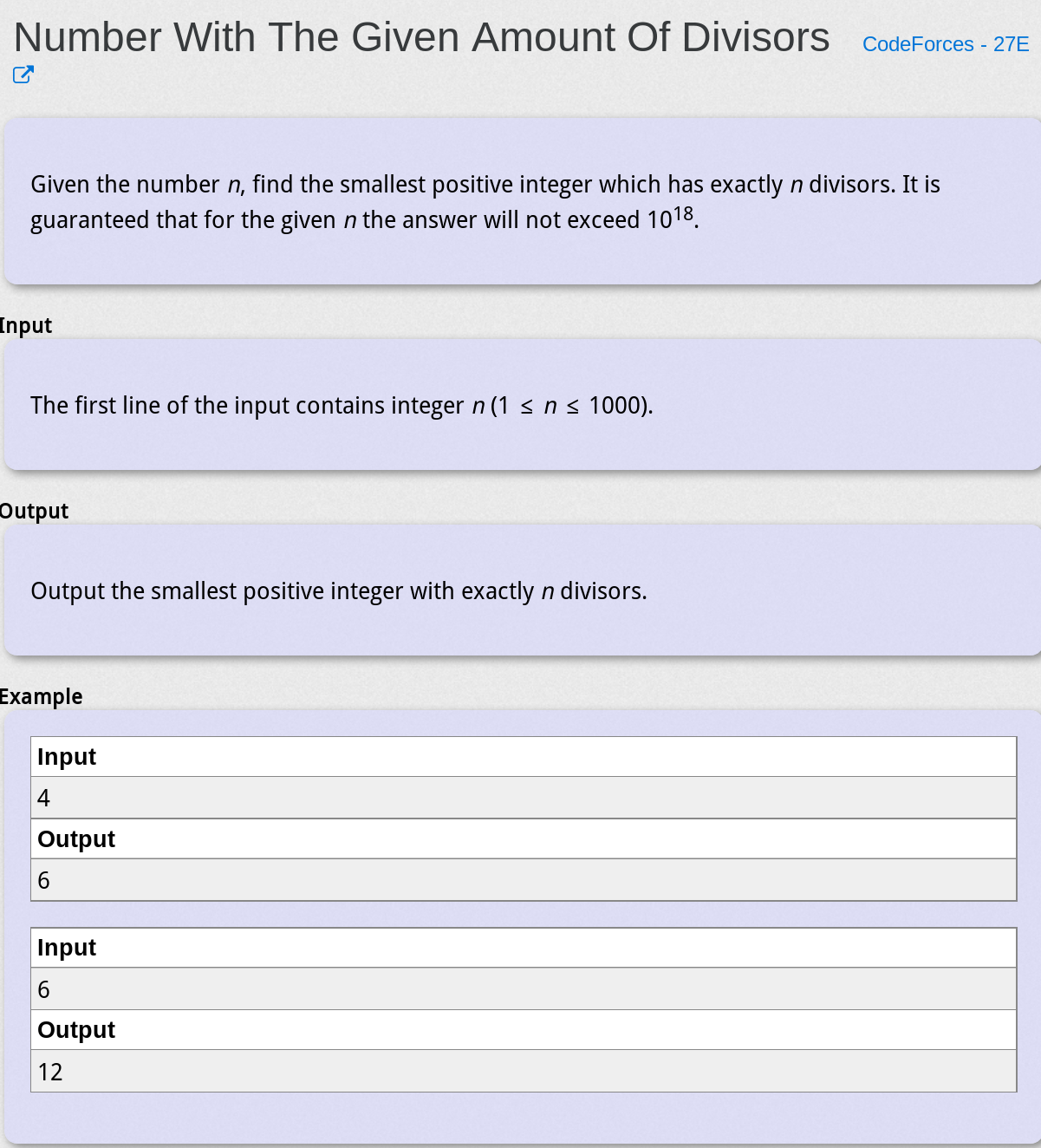
Number With The Given Amount - CodeForces-27E

题目大意
求最小的恰好有n个因子的正整数

思路
模板题

  #include <iostream>
  #include <cstdio>
  #include <algorithm>
  #include <cstring>
  using namespace std;
  typedef long long ll;
  typedef unsigned long long ull;
  const ull INF = ~0ull;

  int prime[18]       = {0, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 57};
  int prime_nums[19]  = {1 << 6, 0};

  void dfs(int depth, int cnt, ull num, int& n, ull& ans){
      if(cnt > n)     return;         //枚举超过所需的n，直接返回，剪枝
      if(cnt == n){                   //cnt == n时，更新最小值
          ans = min(ans, num);
      }
      for(int i = 1; i <= prime_nums[depth - 1]; i++){        //剪枝，因为 t[i+1] > t[i]
          if(num > (ull)1e18/prime[depth])      break;        //超过题目范围剪枝
          prime_nums[depth] = i;                              //更新t[i]，为 t[i+1] 的剪枝做准备
          num*=prime[depth];                                  //更新num值
          dfs(depth + 1, cnt*(i + 1), num, n, ans);           //cnt传的是 cnt*(i+1)，因为1是不算的，要往后挪一位
      }
      prime_nums[depth] = 0;
  }

  int main(){
      int n;
      while(~scanf("%d", &n)){
          ull ans = INF;
          dfs(1, 1, 1, n, ans);
          printf("%lld\n", ans);
      }
  }


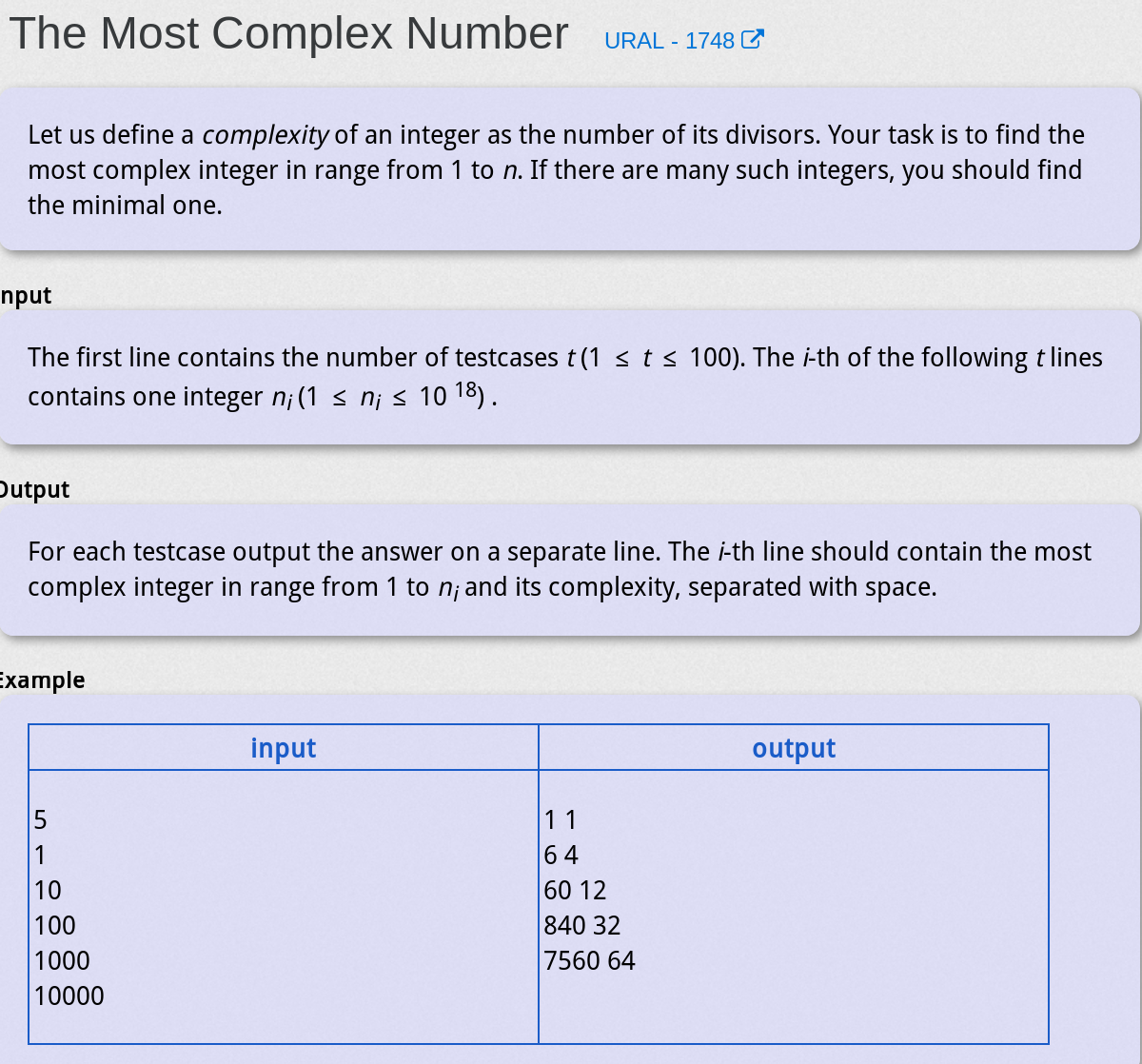
The Most Complex Number - URAL-1748

题目大意
求小于n的反素数，输出数值和因子数

思路
模板题，和上题十分类似

  #include <iostream>
  #include <cstdio>
  #include <algorithm>
  #include <cstring>
  using namespace std;
  typedef long long ll;
  typedef unsigned long long ull;
  const ull INF = ~0ull;

  ull prime[18]       = {0, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 57};
  ull prime_nums[19]  = {1 << 10, 0};

  void dfs(int depth, ull cnt, ull num, ull& upper, ull& max_num, ull& ans){  //传入的n作为上界
      if(cnt > max_num || (cnt == max_num && ans > num)){   //因子数大于 或 因子数相同但值小则更新
          ans = num;
          max_num = cnt;
      }
      for(ull i = 1; i <= prime_nums[depth - 1]; i++){
          if(num > upper/prime[depth])     break;
          prime_nums[depth] = i;
          num*=prime[depth];
          dfs(depth + 1, cnt*(i + 1), num, upper, max_num, ans);
      }
      prime_nums[depth] = 0;
  }

  int main(){
      int t;
      scanf("%d", &t);
      while(t--){
          ull n;
          ull ans = INF;
          ull max_num = 0;
          scanf("%lld", &n);
          dfs(1, 1, 1, n, max_num, ans);
          printf("%lld %lld\n", ans, max_num);
      }
  }


ucyhf - CodeForces-171F

题目大意
题干也是题

思路
看到有题解标题写“千古神题”笑出声，一点儿也不过分
首先拿题干跑循环，当整体偏移10的时候就可以看见题干，求的是Emirp序列第d位的值
那就素数打表咯，但是打多少不知道，题干只给了d <= 11184，我自己开了1e6 + 15的数组，跑到1e6的时候刚刚好溢出，此时刚好跑到11184……
真是精妙呀这题目

  #include <iostream>
  #include <cstdio>
  #include <algorithm>
  #include <cstring>
  using namespace std;
  typedef long long ll;
  typedef unsigned long long ull;
  const ull INF = ~0ull;
  const int N = 1e6 + 15;

  /*  破译题干
  int main(){
      char str[] = "qd ucyhf yi q fhycu dkcruh mxeiu huluhiu yi q tyvvuhudj fhycu dkcruh. oekh jqia yi je vydt jxu djx ucyhf.";
          for(int i = 0; i < strlen(str); i++){
              if(isalpha(str[i]))     str[i] = ((str[i] - 'a') + 10)%26 + 'a';
          }
          puts(str);
  }
  */

  bool used[N];
  int a[N], apos;

  void init(){
      memset(used, true, sizeof(used));
      apos = 1;
      used[0] = used[1] = false;
      for(int i = 2; i < N; i++){
          if(used[i]){
              for(int j = 2; i*j < N; j++){
                  used[i*j] = false;
              }
          }
      }
  }

  int reverse(int x){
      int ans = 0;
      while(x){
          ans = ans*10 + x%10;
          x /= 10;
      }
      return ans;
  }

  int main(){
      init();
      int n = 0;
      for(int i = 2; n < 11184; i++){
          int x = i;
          int y = reverse(x);
          if(x != y && used[x] && used[y]){
              a[apos++] = x;
              n++;
          }
      }

      int in;
      while(~scanf("%d", &in)){
          printf("%d\n", a[in]);
      }
      return 0;
  }