线段树的单点更新
前言
这次线段树这个部分原定3.24发,硬是拖到了今天,比较难啃,而且好像还有4个点没啃T^T
- 线段树 入门
http://blog.csdn.net/zearot/article/details/52280189 - 线段树 详解
https://www.cnblogs.com/AC-King/p/7789013.html - 线段树 约瑟夫环
http://blog.csdn.net/acceptedxukai/article/details/6926431 - 线段树
https://wenku.baidu.com/view/71fc1659ba1aa8114431d97b.html
不会做的题
- Buy Tickets - POJ - 2828
- Points - CodeForces - 19D
敌兵布阵 - HDU 1166
 题目大意
题目大意
此处省略1e9个字
思路
单点更新的模板题来着的
#include <cstdio>
#include <cmath>
#include <climits>
#include <cstring>
#include <iostream>
#define lson l, m, rt << 1 //经常用所以用define
#define rson m + 1, r, rt << 1 | 1
using namespace std;
const int N = 50005;
int sum[N << 2], add[N << 2];
int a[N];
void pushUp(int rt) { sum[rt] = sum[rt << 1] + sum[rt << 1 | 1]; } //本题线段树维护的是区间和
void build(int l, int r, int rt = 1){
if(l == r){
sum[rt] = a[l];
return;
}
int m = (l + r) >> 1;
build(lson); //递归建树
build(rson);
pushUp(rt); //更新信息
}
void update(int p, int val, int l, int r, int rt = 1){
if(l == r){
sum[rt] += val; //更新
return;
}
int m = (l + r) >> 1;
if(p <= m) update(p, val, lson); //找到p点在树中的位置
else update(p, val, rson);
pushUp(rt);
}
int query(int ql, int qr,int l, int r, int rt = 1){
if(ql <= l && r <= qr){ //[l,r]在[ql,qr]中则返回[l,r]中的区间和,剩下部分怎么办?
return sum[rt]; //(接上句)交由其他递归去完成
}
int m = (l + r) >> 1;
int ans = 0;
if(ql <= m) ans += query(ql, qr, lson);
if(qr > m) ans += query(ql, qr, rson);
return ans;
}
int main(){
int t;
char ops[10];
scanf("%d", &t);
for(int caseno = 1; caseno <= t; caseno++){
int n;
scanf("%d", &n);
for(int i = 1; i <= n; i++){
scanf("%d", &a[i]);
}
build(1, n);
printf("Case %d:\n", caseno);
int a, b;
while(scanf("%s", ops)){
if(strcmp(ops, "End") == 0) break;
scanf("%d%d", &a, &b);
if(strcmp(ops, "Query") == 0){
printf("%d\n", query(a, b, 1, n));
}
if(strcmp(ops, "Add") == 0){
update(a, b, 1, n);
}
if(strcmp(ops, "Sub") == 0){
update(a, -b, 1, n);
}
}
}
return 0;
}
Billboard - HDU 2795
 题目大意
题目大意
要在h*w的公告牌上贴1*wi的公告,尽量贴在上面,在此基础上尽量贴在左边,给定每一个wi,求它贴在第几行
思路
一开始看似乎和线段树没什么关系……
不过想想,我们可以用线段树维护每一行剩下多少,然后维护区间最大值,如果最大值都小过现在要贴的公告,那就不要递归那个子树就行,然后优先递归左子树
#include <iostream>
#include <cstdio>
#include <algorithm>
#define lson l, m, rt << 1
#define rson m + 1, r, rt << 1 | 1
typedef long long ll;
const int N = 200005;
const ll INF = 0x3f3f3f3f;
using namespace std;
int sum[N << 2];
void pushUp(int rt) { sum[rt] = max(sum[rt << 1], sum[rt << 1 | 1]); }
void build(int val, int l, int r, int rt = 1){
if(l == r){
sum[rt] = val;
return;
}
int m = (l + r) >> 1;
build(val, lson);
build(val, rson);
pushUp(rt);
}
void update(int p, int val, int l, int r, int rt = 1){
if(l == r){
sum[rt] -= val;
return;
}
int m = (l + r) >> 1;
if(p <= m) update(p, val, lson);
else update(p, val, rson);
pushUp(rt);
}
int query(int val, int l, int r, int rt = 1){
if(l == r){
return sum[rt] >= val ? l : -1; //小于val就返回-1
}
int m = (l + r) >> 1;
int ans = -1; //当下面两个都跑不出结果时可返回-1
if(sum[rt << 1] >= val) ans = query(val, lson); //优先跑左子树,在val不超过左子树区间最小值的情况下
if(ans <= 0 && sum[rt << 1 | 1] >= val) ans = query(val, rson); //有答案了就不用再跑了,没答案也要满足val不超过有子树最小值
return ans;
}
int main(){
int h, w, q;
while(~scanf("%d%d%d", &h, &w, &q)){
h = min(h, q); //一点点小坑,题目给的h的范围很大,但是只要q和h取最小就可以了,q的上界足够小能开数组
build(w, 1, h);
while(q--){
int val, ans;
scanf("%d", &val);
ans = query(val, 1, h);
if(ans > 0){
update(ans, val, 1, h);
}
printf("%d\n", ans);
}
}
return 0;
}
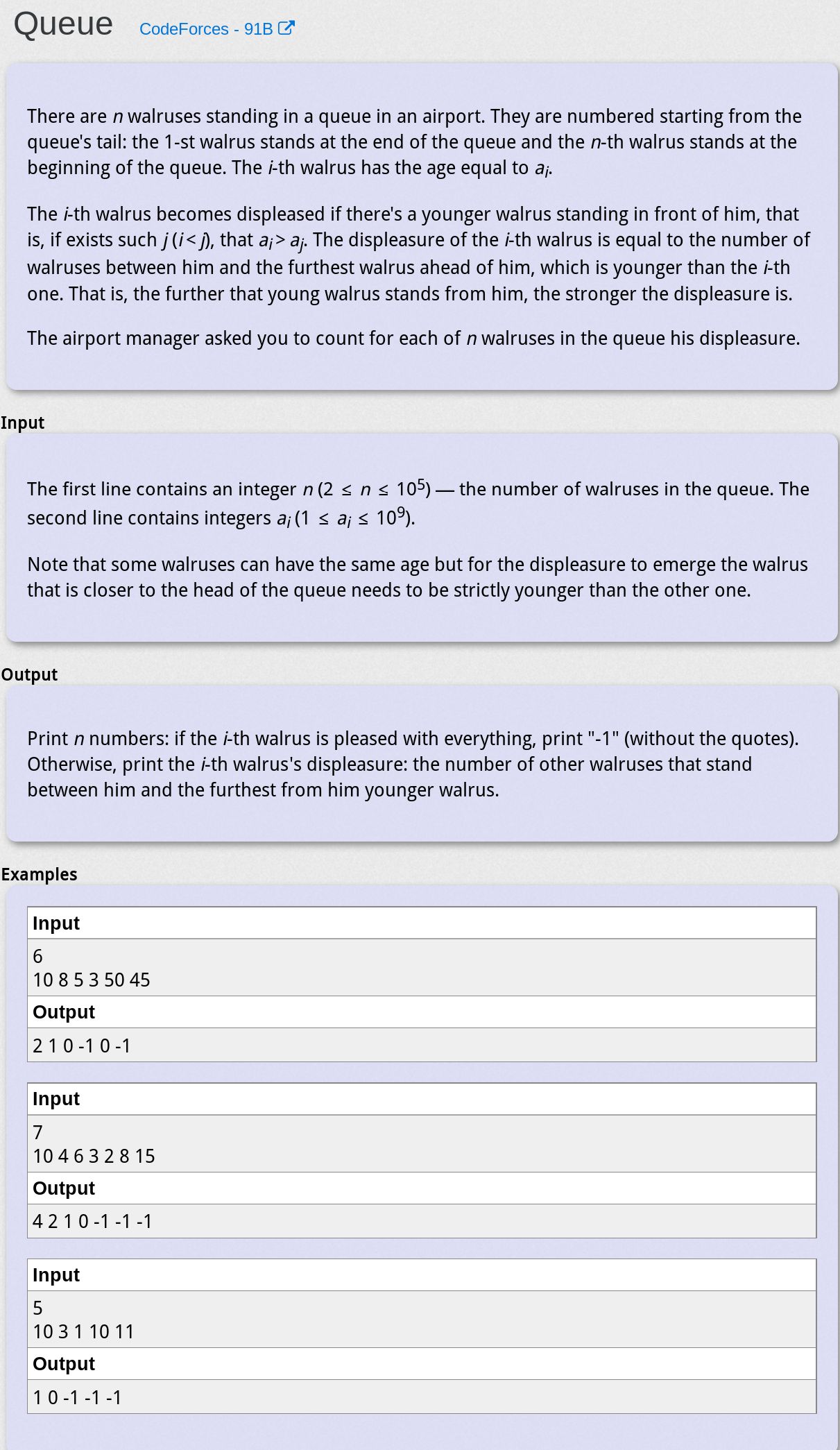
Queue - CodeForces 91B
 题目大意
题目大意
给定一个数组,如果存在i < j但是ai > aj,则i对应的值为 j - i - 1 的最大值(也就是说j取最大能满足ai > aj的),现求出每个i的对应值
思路
用线段树维护一下每个区间段内的最小值,那么查询时便无需查询ai < sum[rt]的部分,可以快速得到解
另外本题求最大的j,所以优先递归右子树,和上题类似
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <vector>
#define lson l, m, rt << 1
#define rson m + 1, r, rt << 1 | 1
#define mid int m = (l + r) >> 1
typedef long long ll;
const int N = 1e5 + 15;
const ll INF = 0x3f3f3f3f;
using namespace std;
int a[N], sum[N << 2], ans[N];
void pushUp(int rt){ sum[rt] = min(sum[rt << 1], sum[rt << 1 | 1]); }
void build(int l, int r, int rt = 1){
if(l == r){
sum[rt] = a[l];
return;
}
mid;
build(lson);
build(rson);
pushUp(rt);
}
int query(int p, int val, int l, int r, int rt = 1){
if(l == r){
return l;
}
mid;
if(p > m || sum[rt << 1 | 1] < val) return query(p, val, rson);
else return query(p, val, lson);
}
int main(){
int n;
while(~scanf("%d", &n)){
for(int i = 1; i <= n; i++){
scanf("%d", &a[i]);
}
build(1, n);
for(int i = 1; i <= n; i++){
printf((i < n ? "%d " : "%d\n"), query(i, a[i], 1, n) - i - 1);
}
}
return 0;
}
Who Gets the Most Candies - POJ-2886
 题目大意
题目大意
有N个小孩围成一圈,他们的编号顺时针编号从1到N,每个小孩手上有一张写着整数的卡片,现在从第k个小孩开始出圈。第k个小孩手上的卡片假设为A,如果A是正数,则下一个出圈的小孩为从第k个小孩开始的顺时针方向的第A个,如果是负数,则是逆时针方向的第A个。现在第i个出圈的小孩可以获得f(i)个糖果,f(i)为i的因子数,现在问谁获得的苹果最多?(如果有多个出圈的小孩获得同样数量的苹果,取最前面的小孩)
思路
啃了线段树单点更新 + 线段树模拟约瑟夫环 + 反素数后,这题就没那么难
本质上本题求 1 - N 的反素数,根据题的范围可以离线打表
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;
/* 离线打表法
const int N = 500000 + 5;
int a[N];
int anti_prime[N], anti_prime_cnt[N], pos;
int prime[18] = {0, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 57};
void dfs(int depth, int cnt, int num){
if(a[num] < cnt){
a[num] = cnt;
}
for(int i = 1; i <= 30; i++){
if(num > N/prime[depth]) break;
num *= prime[depth];
dfs(depth + 1, cnt*(i + 1), num);
}
}
int main(){
memset(a, 0, sizeof(a));
dfs(1, 1, 1);
pos = 0;
int x = 0;
for(int i = 1; i < N; i++){
if(a[i] > x){
anti_prime[pos] = i;
anti_prime_cnt[pos++] = a[i];
x = a[i];
}
}
printf("int anti_prime[%d] = {", pos);
printf("%d", anti_prime[0]);
for(int i = 1; i < pos; i++){
printf(", %d", anti_prime[i]);
}
printf("};\n");
printf("int anti_prime_cnt[%d] = {", pos);
printf("%d", anti_prime_cnt[0]);
for(int i = 1; i < pos; i++){
printf(", %d", anti_prime_cnt[i]);
}
printf("};\n");
return 0;
}*/
#define lson l, m, rt << 1
#define rson m + 1, r, rt << 1 | 1
#define mid int m = (l + r) >> 1
const int N = 500000 + 5;
int sum[N << 2], a[N << 2], b[N << 2];
int anti_prime[35] = {1, 2, 4, 6, 12, 24, 36, 48, 60, 120, 180, 240, 360, 720, 840, 1260, 1680, 2520, 5040, 7560, 10080, 15120, 20160, 25200, 27720, 45360, 50400, 55440, 83160, 110880, 166320, 221760, 277200, 332640, 498960};
int anti_prime_cnt[35] = {1, 2, 3, 4, 6, 8, 9, 10, 12, 16, 18, 20, 24, 30, 32, 36, 40, 48, 60, 64, 72, 80, 84, 90, 96, 100, 108, 120, 128, 144, 160, 168, 180, 192, 200};
char str[N][15], pos;
int val[N];
void pushUp(int rt) { sum[rt] = sum[rt << 1] + sum[rt << 1 | 1]; }
void build(int l, int r, int rt = 1){
a[rt] = l;
b[rt] = r;
if(l == r){
sum[rt] = 1;
}else{
mid;
build(lson);
build(rson);
pushUp(rt);
}
}
int update(int p, int rt = 1){
int ans;
if(a[rt] == b[rt]){
sum[rt] = 0;
return a[rt];
}else{
if(p <= sum[rt << 1]) ans = update(p, rt << 1);
else ans = update(p - sum[rt << 1], rt << 1 | 1); //进入右子树要变换相对位置
}
pushUp(rt);
return ans;
}
void init(){
pos = 0;
}
void solve(int n, int start){
init();
build(1, n);
int m = start;
int seq = 1; //表示当前序列的第几个人,不代表编号
int pend = upper_bound(anti_prime, anti_prime + 35, n) - 1 - anti_prime;
int end = anti_prime[pend];
int t = 0; //循环次数控制
int ans;
while(t < end){
seq--;
if(m >= 0){ //非负则是 m - 1 个,因为第seq个人GG后,它的下一个人变成第seq个人,本身就是1了
seq = ((seq + m - 1)%sum[1] + sum[1])%sum[1];
}else{ //负则是 m 个
seq = ((seq + m)%sum[1] + sum[1])%sum[1];
}
seq++;
int k = update(seq); //更新顺便找编号
m = val[k];
t++;
if(t == end) ans = k;
}
printf("%s %d\n", str[ans], anti_prime_cnt[pend]);
}
int main(){
int n, start;
while(~scanf("%d%d", &n, &start)){
for(int i = 1; i <= n; i++){
scanf("%s%d", str[i], &val[i]);
}
solve(n, start);
}
}


