字典树的静态建树
前言
数学大战即将来袭!所以写的少一些,还没怎么看数学呢!
字典树又称前缀树,顾名思义,用公共前缀来存储字符串,优点是效率高,但是缺点也明显,就是每个节点都要有一个next指针数组,极大的浪费内存
字典树可以动态建树,即每个节点都是new出来的,也可以静态建树,即用一个tot变量为每个节点连上一个node数组中的元素,因为ACM追求时间效率,所以本文通篇采用静态建树
- 动态建树与静态建树
https://www.cnblogs.com/George1994/p/6346790.html - Trie树详解
https://segmentfault.com/a/1190000008877595
不会做的题
- POJ 2513 - Colored Sticks
- HDU 2846 - Repository
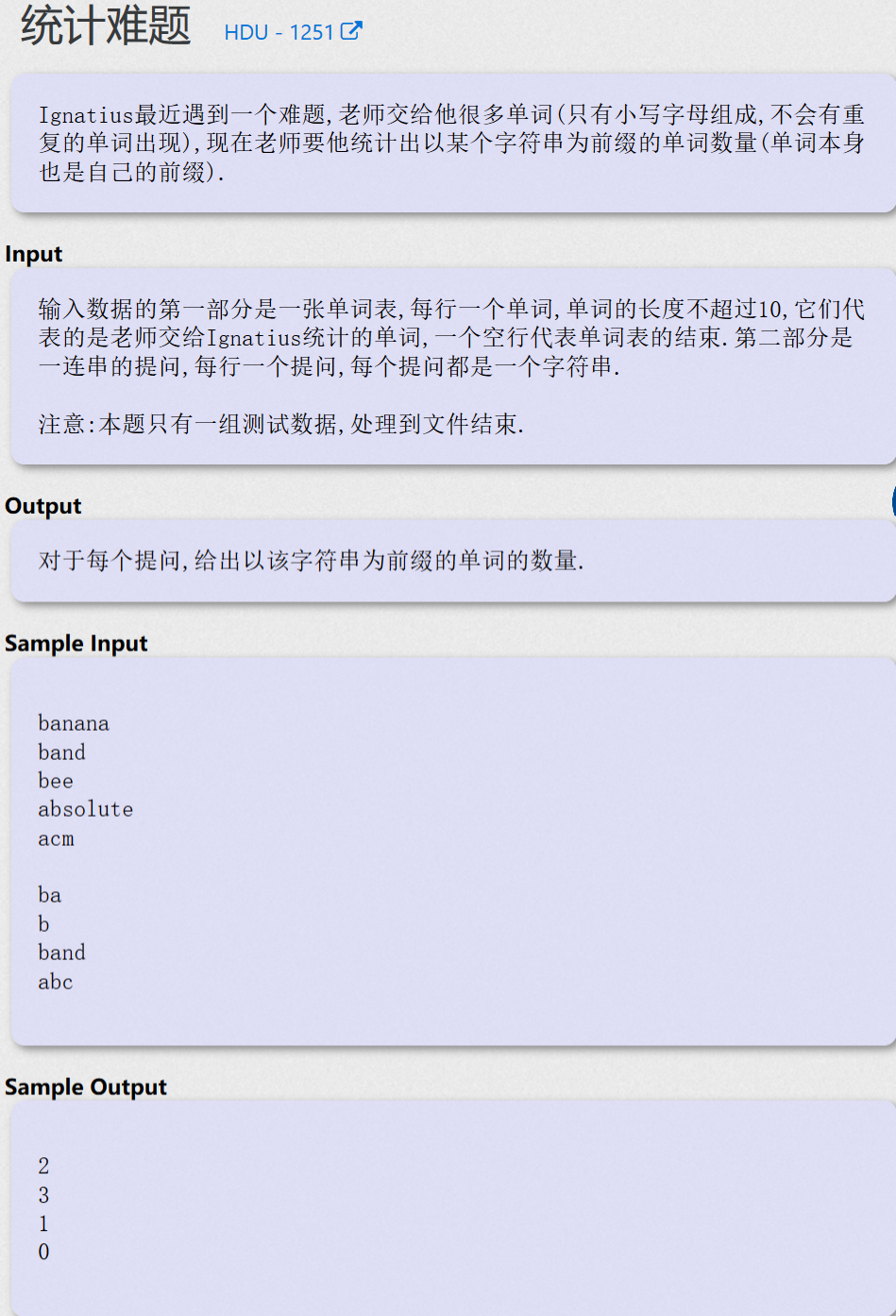
统计难题 - HDU 1251
 题目大意
题目大意
OMIT!
思路
这道题太邪门了……选G++过不了题,会Memory Limit Exceeded……选C++才过了
还有,不给范围,天!诛!地!灭!
这道题就是所走过之处,cnt++,然后查询的时候输出cnt就完事了
不过这题get了个点是gets的话,如果为空行,那么str[0]会被它改为NULL
#include <cstdio>
#include <cstring>
using namespace std;
const int N = 5e5 + 15;
int cnt[N]; //计数
int nxt[N][26]; //next指针
char str[12];
int tot; //节点分配
inline void init(){
tot = 1; //从1开始,因为0给了root节点
memset(cnt, 0, sizeof(cnt));
memset(nxt[0], -1, sizeof(nxt));
}
void push(char* s){
int p = 0;
for( ; * s; s++){
int idx = * s - 'a';
if(nxt[p][idx] == -1){ //如果下一个节点不存在
nxt[p][idx] = tot++; //分配节点
}
cnt[nxt[p][idx]]++; //走过之处cnt++
p = nxt[p][idx]; //走向下一个节点
}
}
int query(char* s){
int p = 0;
for( ; *s; s++){
int idx = * s - 'a';
if(nxt[p][idx] == -1) return 0; //没走完直接返回0
p = nxt[p][idx];
}
return cnt[p];
}
int main(){
init();
while(gets(str)){
if(!(*str)) break;
push(str);
}
while(gets(str)){
printf("%d\n", query(str));
}
}
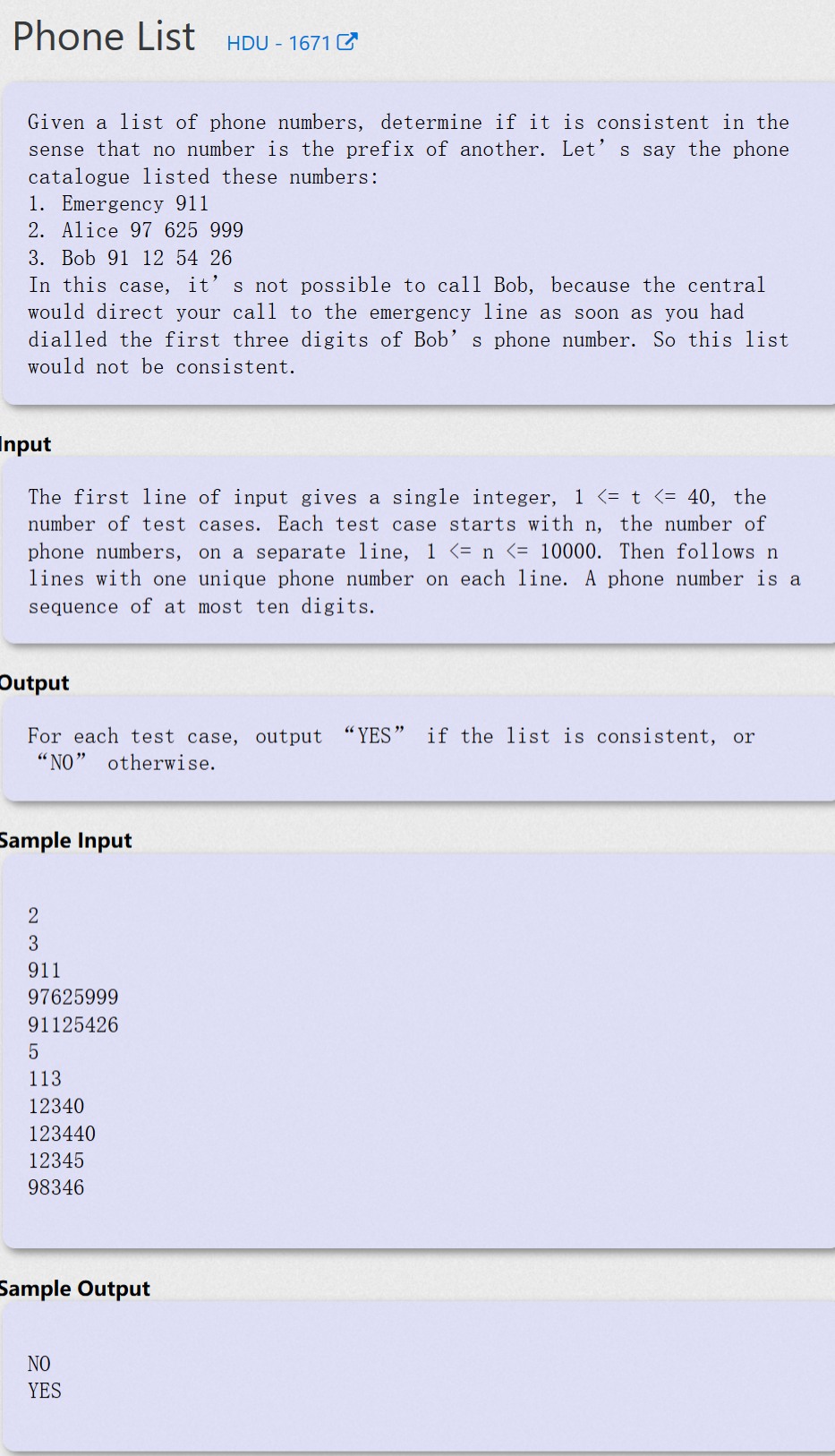
Phone List - HDU 1671
 题目大意
题目大意
给定电话号码,求是否任意一个电话号码都不是其他电话号码的前缀
思路
模板题
一边加入单词一边建树,那么“任意一个电话号码都不是其他电话号码的前缀”就体现在:
① 这个单词不是别的单词的前缀: 加入过程中有new一个新结点,说明一定不是别的单词的前缀
② 别的单词不是这个单词的前缀: 加入过程中没经过end == true的节点,说明别的单词一定不是它的前缀
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 1e5 + 15;
bool mend[N];
int nxt[N][10];
int tot; //控制节点的分配
inline void init(){
tot = 1;
memset(mend, false, sizeof(mend));
memset(nxt[0], -1, sizeof(nxt));
}
inline bool push(char str[]){
bool ans = false;
bool after = true;
int p = 0;
for( ; * str; str++){
int idx = * str - '0';
if(nxt[p][idx] == -1){ //如果没有这个节点就创建
nxt[p][idx] = tot++;
after = false; //后面肯定无节点
}
ans |= (mend[nxt[p][idx]]); //判断是否经过某个单词的end
p = nxt[p][idx];
}
mend[p] = true;
return (ans == false && after == false);
}
int main(){
char str[12];
int t;
scanf("%d", &t);
while(t--){
bool flag = true;
init();
int n;
scanf("%d", &n);
while(n--){
scanf("%s", str);
if(flag && !push(str)) flag = false;
}
printf("%s\n", flag ? "YES" : "NO");
}
}
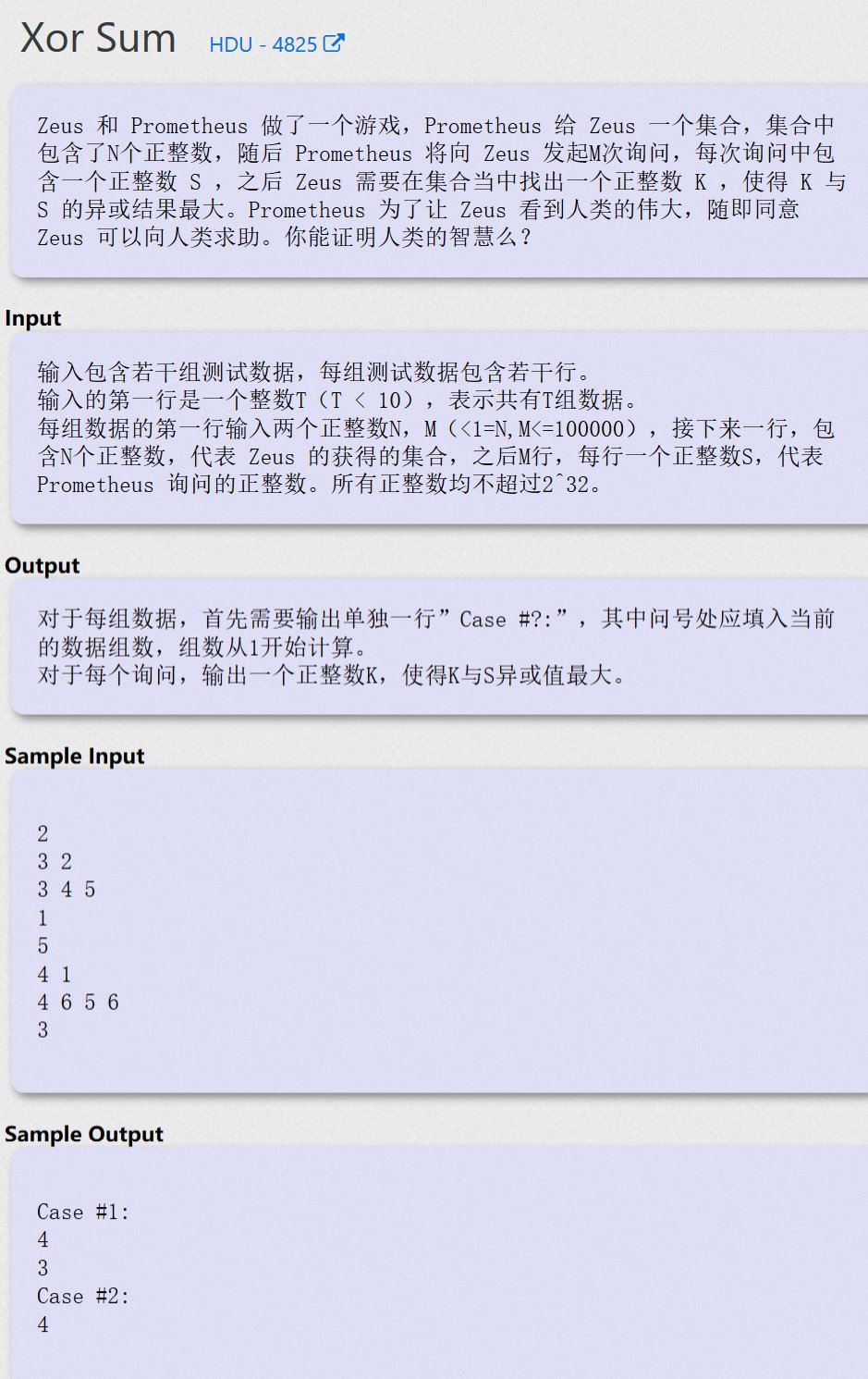
Xor Sum - HDU 4825
 题目大意
题目大意
Omit as well
思路
这题目一开始看上去和Trie树并没有什么关系……
但是不妨想一想,要是异或值最大,就要 每一位都和当前的查询的数的对应位相反
所以可以先把所给集合的每一个数以二进制形式存入树中,查询的数取反后查询,如果有这一位,那么就往下执行,如果没有,那就只能先妥协,走另一边,而另一边是一定有节点的,因为我们的数字都是全部位存进去的,而位只能是0和1,所以集合只要非空,一定有一条边可以走到底,不管它是不是妥协的
#include <cstdio>
#include <cstring>
using namespace std;
const int N = 4e6 + 15;
struct pNode{
unsigned val;
pNode* next[2];
};
pNode node[N];
pNode* root;
int tot;
inline void nodeInit(pNode*& nd){
nd->val = -1;
memset(nd->next, 0, sizeof(nd->next));
}
inline void init(){
tot = 0;
root = &node[tot++];
nodeInit(root);
}
void push(unsigned val){
unsigned b = val;
pNode* p = root;
for(int t = 0; t < 32; t++, b <<= 1){
unsigned idx = ((b >> 31)&1);
pNode*& pnext = p->next[idx];
if(!pnext){
pnext = &node[tot++];
nodeInit(pnext);
}
p->val = val;
p = pnext;
}
p->val = val;
}
int query(unsigned val){
unsigned b = ~val;
pNode* p = root;
for(int t = 0; t < 32; t++, b <<= 1){
unsigned idx = ((b >> 31)&1);
if(p->next[idx]) p = p->next[idx];
else p = p->next[idx^1];
}
return p->val;
}
int main(){
int t;
int caseno = 1;
scanf("%d", &t);
while(t--){
init();
int n, m;
scanf("%d%d", &n, &m);
while(n--){
unsigned v;
scanf("%u", &v);
push(v);
}
printf("Case #%d:\n", caseno++);
while(m--){
unsigned q;
scanf("%u", &q);
printf("%u\n", query(q));
}
}
return 0;
}
T9 - POJ 1451
 题目大意
题目大意
题目太长,很想omit
本题其实就是输入法的9键模式
注意本题中相同前缀的机率是相加的(因为这个WA了 T^T)
就这样,基本Omit!
思路
开个数组保存字典,然后建两棵树
第一棵树插入字符串,所走之处把对应字符串的机率加上去,并且写入对应字符串在字典中的位置,这样就得到了前缀机率相加后的字典树
第二棵树插入字符串对应数字,所走之处不断更新当前机率最大对应的字符串在字典中的位置,并更新节点的最大机率
最后问啥查啥,注意走到str[i] == ‘1’就可以了
(这题真的是模板题嘛?)
#include <cstdio>
#include <cstring>
using namespace std;
const int N = 1000 + 15;
const int M = 100 + 15;
struct pNode{
int p, lv;
pNode* next[26];
};
const int trans[] = {2,2,2,3,3,3,4,4,4,5,5,5,6,6,6,7,7,7,7,8,8,8,9,9,9,9};
char str[N][M];
int lv[N];
pNode node[N], word[N]; //node是字符串对应数字的节点数组,word是字符串节点数组
pNode *root, *wroot;
int tot, wtot;
inline void nodeInit(pNode*& nd){
memset(nd->next, 0, sizeof(nd->next));
nd->p = -1, nd->lv = 0;
}
inline void init(){
tot = 0, wroot = 0;
root = &node[tot++];
wroot = &word[wtot++];
nodeInit(root);
nodeInit(wroot);
}
void build_word(int n){
for(int i = 0; i < n; i++){
char* s = str[i];
pNode* p = wroot;
while(*s){
int idx = *s - 'a';
pNode*& pnext = p->next[idx];
if(!pnext){
pnext = &word[wtot++];
nodeInit(pnext);
}
pnext->p = i;
pnext->lv += lv[i];
p = pnext;
s++;
}
}
}
void build(int n){
build_word(n);
for(int i = 0; i < n; i++){
char* s = str[i];
pNode* p = root;
pNode* wp = wroot;
while(*s){
int idx = trans[* s - 'a'];
pNode*& pnext = p->next[idx];
pNode*& wpnext = wp->next[* s - 'a'];
if(!pnext){
pnext = &node[tot++];
nodeInit(pnext);
}
if((pnext->lv) < (wpnext->lv)){
pnext->lv = wpnext->lv;
pnext->p = wpnext->p;
}
p = pnext;
wp = wpnext;
s++;
}
}
}
void query(char s[]){
int i;
pNode* p = root;
for(i = 0; s[i] != '1'; i++){
int idx = s[i] - '0';
pNode*& pnext = p->next[idx];
if(!pnext) break;
for(int j = 0; j <= i; j++) putchar(str[pnext->p][j]);
puts("");
p = pnext;
}
while(s[i] != '1'){
puts("MANUALLY");
i++;
}
}
int main(){
char q[M];
int t;
int caseno = 1;
scanf("%d", &t);
while(t--){
init();
int n, m;
scanf("%d", &n);
for(int i = 0; i < n; i++){
scanf("%s%d", str[i], &lv[i]);
}
build(n);
scanf("%d", &m);
printf("Scenario #%d:\n", caseno++);
while(m--){
scanf("%s", q);
query(q);
puts("");
}
puts("");
}
}


