后缀自动机(SAM)
前言
本来以为能20号发,太高估自己了 T^T,个人目前对于SAM的理解可能连60%都不到 QAQ
本文解题都在HihoCoder有,各位有需要自己到HihoCoder看解题提示,篇幅有限(主要是懒)就没放在里面
- SAM
HihoCoder
https://blog.csdn.net/wmdcstdio/article/details/44780707
https://kyleyoung-ymj.github.io/Suffix-Automaton/
https://wenku.baidu.com/view/90f22eec551810a6f4248606.html
hihoCoder 1445 : 后缀自动机二·重复旋律5
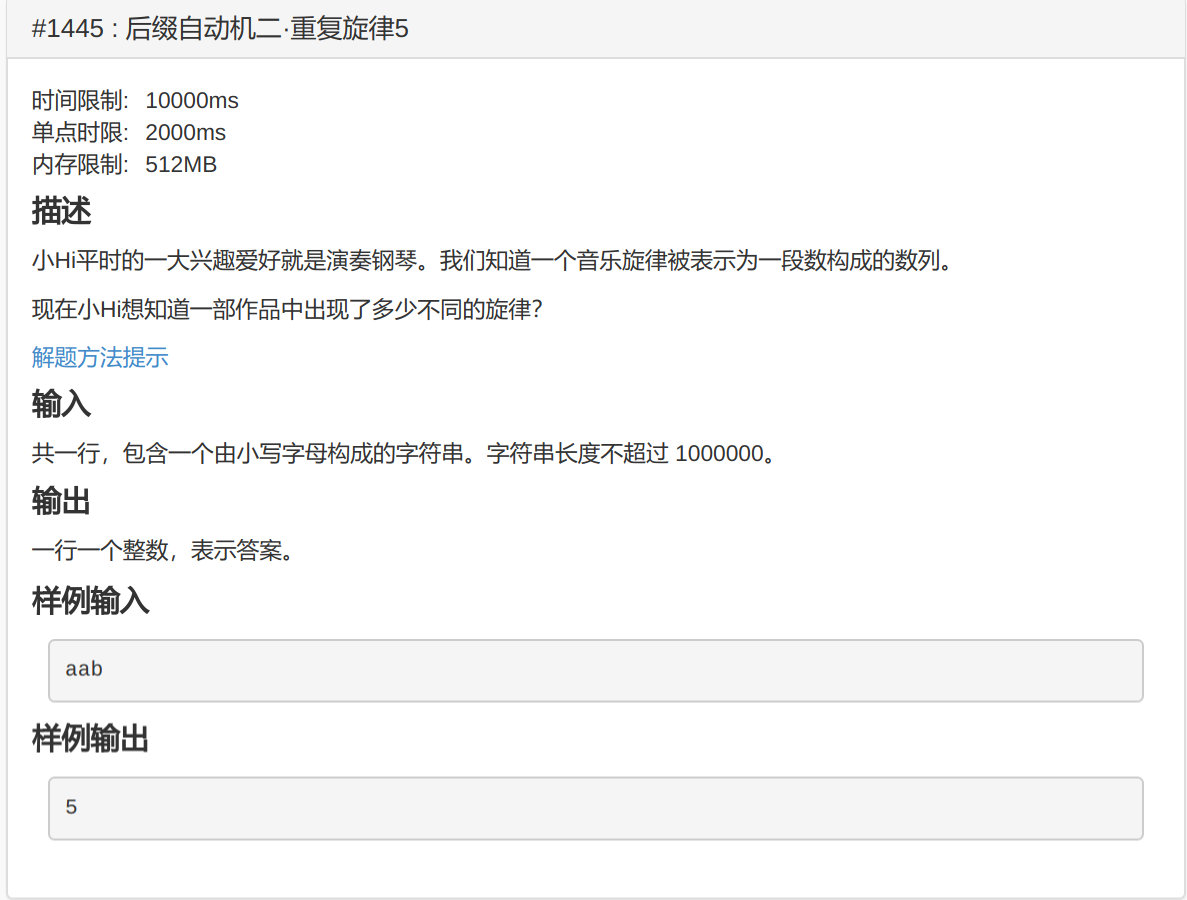
#include <cstdio>
#include <cstring>
using namespace std;
typedef long long ll;
const int N = (int)1e6 + 15;
char str[N];
struct SuffixMaton{
// SZ: 字符集大小
// tot: 静态分配节点ID
// lst: 上一个节点ID
// slink: suffix link,后缀链接
// len: 状态中的maxlen
// trans: 状态转移
const static int SZ = 26;
int tot, lst;
int slink[N << 1], len[N << 1], trans[N << 1][SZ];
// NewNode函数:分配新节点,需要清空trans
int NewNode(){
int ret = ++tot;
memset(trans[ret], 0, sizeof(trans[ret]));
return ret;
}
void init(){
tot = 0;
lst = NewNode(); //分配S状态的节点
slink[lst] = len[lst] = 0; //把S状态的slink设为NULL,len设为0
}
void push(int val){
int p = lst, np = NewNode(); //为新字符新建一个状态np
len[np] = len[p] + 1; //新状态maxlen为前一个状态maxlen + 1,这是显然的
//对于lst到root(S状态)的路径中,无经val转移的,直接令其等于np
//最终如果转移到NULL,那么状态np的suffix link应连接到S状态
for(; p && trans[p][val] == 0; p = slink[p]) trans[p][val] = np;
if(p == 0) slink[np] = 1;
else{
//否则,则说明子串存在
//记状态q为trans[p][val],即p经过val转移的状态
//如果len[q] = len[p] + 1,则说明可以直接将slink连到q
int q = trans[p][val];
if(len[q] == len[p] + 1) slink[np] = q;
else{
//否则,不能直接将slink连接到那个里面
//新建状态q的分割状态q,将 <= len[p] + 1的部分以及q的其他属性复制到那个状态里面
//将q和np的slink连接到nq
int nq = ++tot;
slink[nq] = slink[q];
len[nq] = len[p] + 1;
memcpy(trans[nq], trans[q], sizeof(trans[q]));
slink[q] = slink[np] = nq;
//重定向原来指向q的
for(trans[p][val] = nq, p = slink[p]; p && trans[p][val] == q; p = slink[p]) trans[p][val] = nq;
}
}
lst = np;
}
};
SuffixMaton sam;
int main(){
while(~scanf("%s", str)){
sam.init();
for(int i = 0; str[i]; i++){
sam.push(str[i] - 'a');
}
ll ans = 0;
for(int i = 2; i <= sam.tot; i++){
ans += (sam.len[i] - sam.len[sam.slink[i]]);
}
printf("%lld\n", ans);
}
}
hihoCoder 1449 : 后缀自动机三·重复旋律6
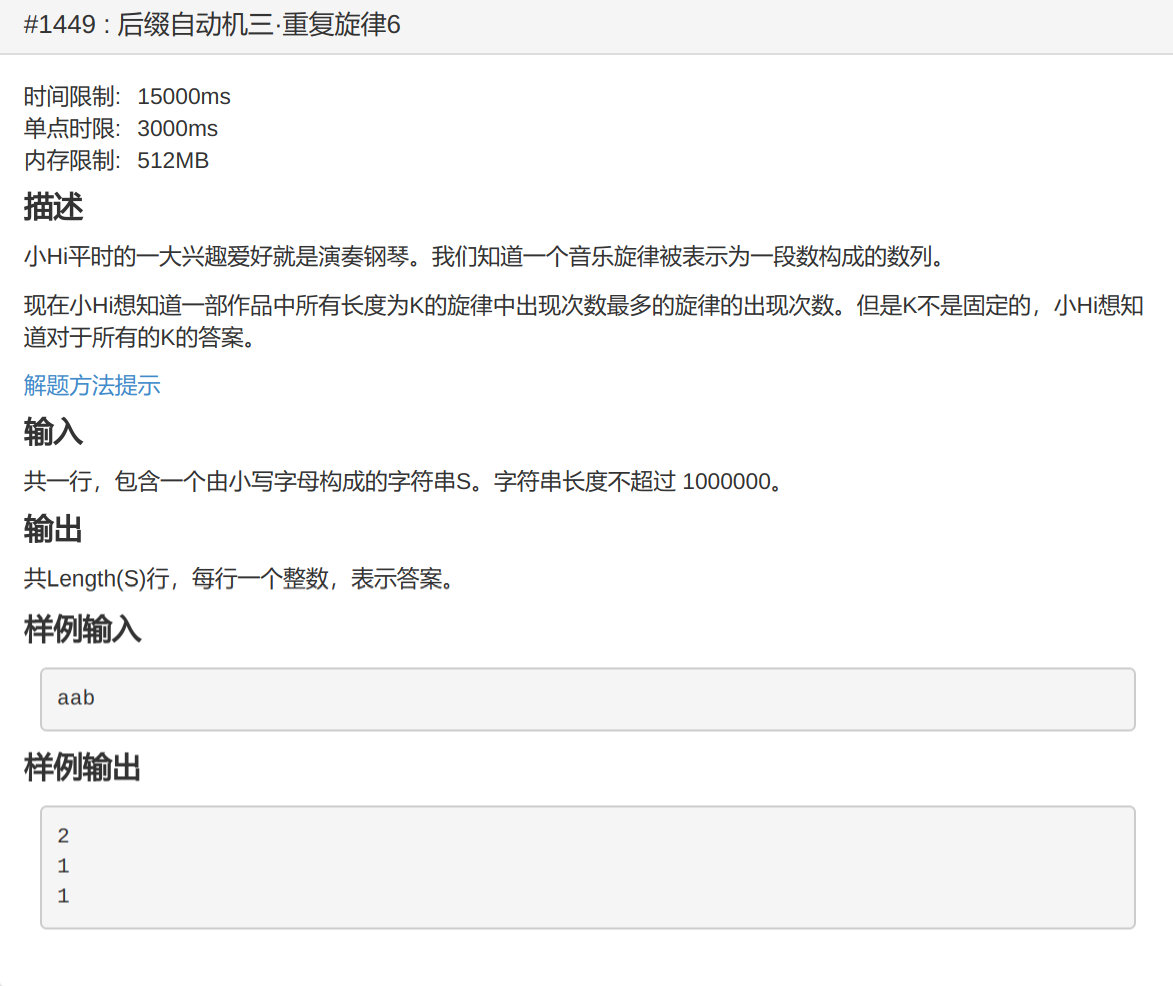
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;
const int N = 1e6 + 15;
char str[N];
struct SuffixMaton{
const static int SZ = 26;
int tot, lst;
int slink[N << 1], len[N << 1], trans[N << 1][SZ], endsz[N << 1];
int NewNode(){
int ret = ++tot;
memset(trans[ret], 0, sizeof(trans[ret]));
return ret;
}
void init(){
tot = 0;
lst = NewNode();
slink[lst] = len[lst] = 0;
endsz[0] = 0; // 空节点不为绿色
endsz[1] = 1; // 非空节点为绿色
}
void push(int val){
int p = lst, np = NewNode();
len[np] = len[p] + 1;
endsz[np] = 1;
for(; p && trans[p][val] == 0; p = slink[p]) trans[p][val] = np;
if(p == 0) slink[np] = 1;
else{
int q = trans[p][val];
if(len[q] == len[p] + 1) slink[np] = q;
else{
int nq = ++tot;
endsz[nq] = 0;
slink[nq] = slink[q];
len[nq] = len[p] + 1;
memcpy(trans[nq], trans[q], sizeof(trans[q]));
slink[q] = slink[np] = nq;
for(trans[p][val] = nq, p = slink[p]; p && trans[p][val] == q; p = slink[p]) trans[p][val] = nq;
}
}
lst = np;
}
//利用parent树性质,endpos集合性质,求出 |endpos|
int que[N << 1], idg[N << 1], head, tail;
void topoSort(){
head = tail = 0;
memset(idg, 0, sizeof(idg));
for(int i = 2; i <= tot; i++) idg[slink[i]]++;
for(int i = 1; i <= tot; i++){
if(idg[i] == 0) que[tail++] = i;
}
while(head != tail){
int u = que[head++];
int preu = slink[u];
endsz[preu] += endsz[u];
idg[preu]--;
if(preu && idg[preu] == 0) que[tail++] = preu;
}
}
int ans[N];
void solve(){
memset(ans, 0, sizeof(ans));
topoSort();
int slen = strlen(str);
for(int i = 1; i <= tot; i++){
ans[len[i]] = max(ans[len[i]], endsz[i]);
}
for(int i = slen - 1; i >= 1; i--){
ans[i] = max(ans[i], ans[i + 1]);
}
for(int i = 1; i <= slen; i++){
printf("%d\n", ans[i]);
}
}
};
SuffixMaton sam;
int main(){
while(~scanf("%s", str)){
sam.init();
for(int i = 0; str[i]; i++){
sam.push(str[i] - 'a');
}
sam.solve();
}
}
hihoCoder 1457 : 后缀自动机四·重复旋律7

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;
const int N = 2e6 + 15;
const int MOD = 1e9 + 7;
char str[N];
struct SuffixMaton{
const static int SZ = 11;
int tot, lst;
int slink[N << 1], len[N << 1], trans[N << 1][SZ];
int NewNode(){
int ret = ++tot;
memset(trans[ret], 0, sizeof(trans[ret]));
return ret;
}
void init(){
tot = 0;
lst = NewNode();
slink[lst] = len[lst] = 0;
}
void push(int val){
int p = lst, np = NewNode();
len[np] = len[p] + 1;
for(; p && trans[p][val] == 0; p = slink[p]) trans[p][val] = np;
if(p == 0) slink[np] = 1;
else{
int q = trans[p][val];
if(len[q] == len[p] + 1) slink[np] = q;
else{
int nq = ++tot;
slink[nq] = slink[q];
len[nq] = len[p] + 1;
memcpy(trans[nq], trans[q], sizeof(trans[q]));
slink[q] = slink[np] = nq;
for(trans[p][val] = nq, p = slink[p]; p && trans[p][val] == q; p = slink[p]) trans[p][val] = nq;
}
}
lst = np;
}
int que[N << 1], head, tail;
int cnt[N << 1], idg[N << 1];
ll sum[N << 1];
void topoSort(){
memset(cnt, 0, sizeof(cnt));
memset(idg, 0, sizeof(idg));
memset(sum, 0, sizeof(sum));
//求出trans构成的DAG的入度
for(int u = 1; u <= tot; u++){
for(int val = 0; val < SZ; val++){
if(trans[u][val]) idg[trans[u][val]]++;
}
}
//DAG一开始入度的点必定是S状态
//cnt其实是S状态到该点且不经过val=10的路径数(因为从S状态到任意点的路径是任意一子串),故可递推求出
//sum可根据公式 sum[v] = (sum[v] + sum[u] * 10 + val * cnt[u]) % MOD 递推
//注意经过val=10的点已经跨字符串,不计入
head = tail = 0;
que[tail++] = 1;
cnt[1] = 1;
while(head != tail){
int u = que[head++];
for(int val = 0; val < SZ; val++){
int v = trans[u][val];
if(v == 0) continue;
if(val != 10){
sum[v] = (sum[v] + sum[u] * 10 + val * cnt[u]) % MOD;
cnt[v] += cnt[u];
}
idg[v]--;
if(idg[v] == 0) que[tail++] = v;
}
}
}
ll ans;
void solve(){
topoSort();
ans = 0;
for(int i = 2; i <= tot; i++){
ans = (ans + sum[i]) % MOD;
}
printf("%lld\n", ans);
}
};
SuffixMaton sam;
int main(){
int t;
while(~scanf("%d", &t)){
sam.init();
while(t--){
scanf("%s", str);
for(int i = 0; str[i]; i++) sam.push(str[i] - '0');
if(t > 0) sam.push(10);
}
sam.solve();
}
}
hihoCoder 1465 : 后缀自动机五·重复旋律8
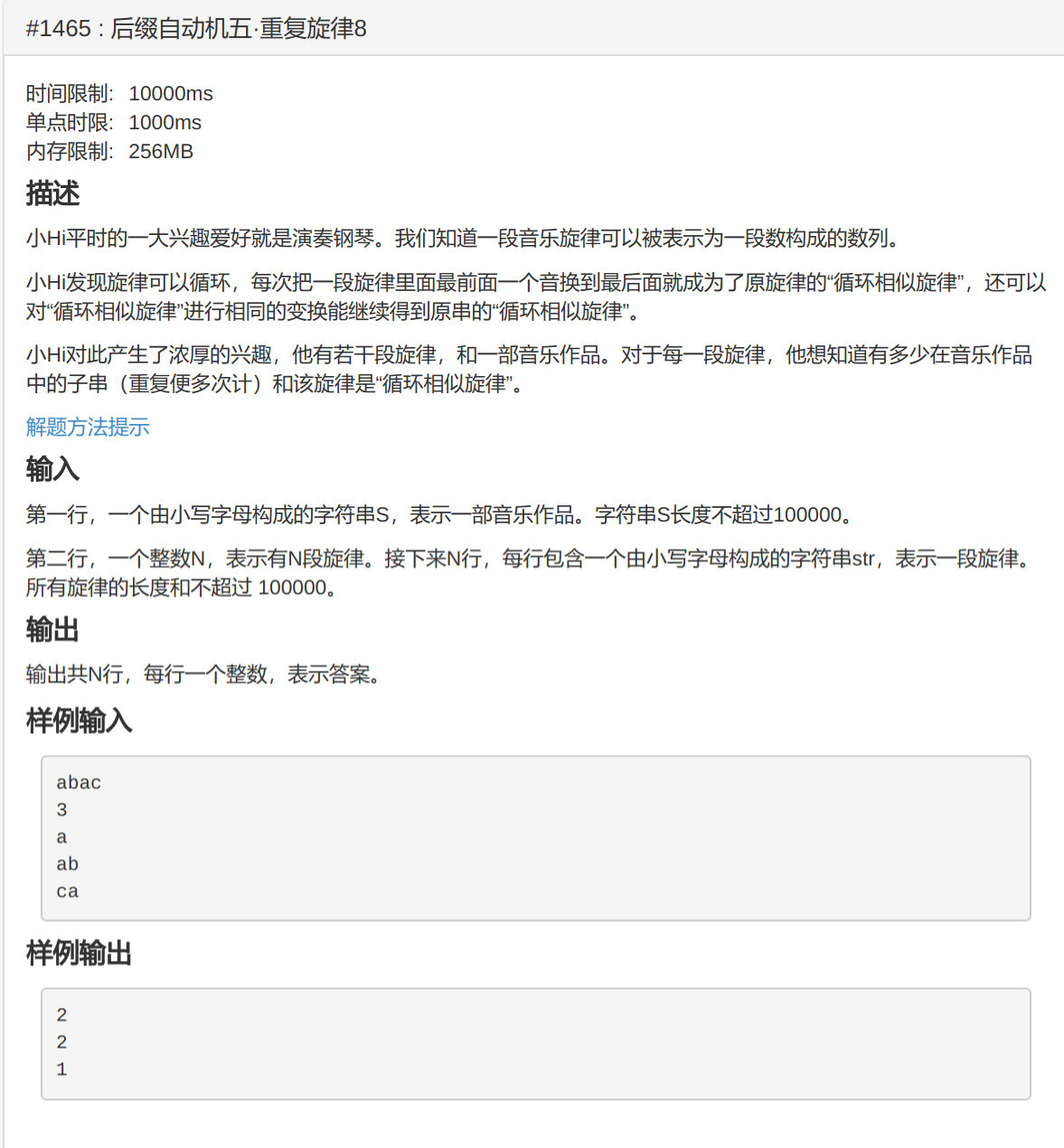
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;
const int N = 2e5 + 15;
char s[N], p[N];
struct SuffixMaton{
const static int SZ = 26;
int tot, lst;
int slink[N << 1], len[N << 1], trans[N << 1][SZ], endsz[N << 1];
int NewNode(){
int ret = ++tot;
memset(trans[ret], 0, sizeof(trans[ret]));
return ret;
}
void init(){
tot = 0;
lst = NewNode();
slink[lst] = len[lst] = 0;
endsz[0] = 0;
endsz[1] = 1;
}
void push(int val){
int p = lst, np = NewNode();
len[np] = len[p] + 1;
endsz[np] = 1;
for(; p && trans[p][val] == 0; p = slink[p]) trans[p][val] = np;
if(p == 0) slink[np] = 1;
else{
int q = trans[p][val];
if(len[q] == len[p] + 1) slink[np] = q;
else{
int nq = ++tot;
endsz[nq] = 0;
slink[nq] = slink[q];
len[nq] = len[p] + 1;
memcpy(trans[nq], trans[q], sizeof(trans[q]));
slink[q] = slink[np] = nq;
for(trans[p][val] = nq, p = slink[p]; p && trans[p][val] == q; p = slink[p]) trans[p][val] = nq;
}
}
lst = np;
}
int que[N << 1], idg[N << 1], head, tail;
void getEndSz(){
head = tail = 0;
memset(idg, 0, sizeof(idg));
for(int i = 2; i <= tot; i++) idg[slink[i]]++;
for(int i = 1; i <= tot; i++){
if(idg[i] == 0) que[tail++] = i;
}
while(head != tail){
int u = que[head++];
int preu = slink[u];
if(preu == 0) continue;
endsz[preu] += endsz[u];
idg[preu]--;
if(preu && idg[preu] == 0) que[tail++] = preu;
}
}
bool used[N << 1];
ll solve(){
int n = strlen(p);
for(int i = 0; i < n; i++) p[i + n] = p[i];
p[n << 1] = 0;
memset(used, false, sizeof(used));
ll ans = 0;
int u = 1, l = 0;
for(int i = 0; p[i]; i++){
while(u != 1 && trans[u][p[i] - 'a'] == 0) u = slink[u], l = len[u];
if(trans[u][p[i] - 'a']) u = trans[u][p[i] - 'a'], l++;
else u = 1, l = 0;
if(l > n){
while(len[slink[u]] >= n) u = slink[u], l = len[u];
}
if(l >= n && !used[u]) ans += endsz[u], used[u] = true;
}
return ans;
}
};
SuffixMaton sam;
int main(){
while(~scanf("%s", s)){
sam.init();
for(int i = 0; s[i]; i++) sam.push(s[i] - 'a');
sam.getEndSz();
int t;
scanf("%d", &t);
while(t--){
scanf("%s", p);
printf("%lld\n", sam.solve());
}
}
}


