Edmonds-Karp算法、Dinic算法、ISAP算法、最大流最小割定理
前言
回家以后学习速度急速下降 QAQ
本文只涉及网络流的基础,真的只有基础…(说难听了叫做只有模板)
- 综合
http://acm.pku.edu.cn/summerschool/gw_netflow.pdf - Dinic
https://www.cnblogs.com/SYCstudio/p/7260613.html
https://baike.baidu.com/item/Dinic%E7%AE%97%E6%B3%95/3956790?fr=aladdin - ISAP
https://www.renfei.org/blog/isap.html
https://www.cnblogs.com/jffifa/archive/2012/05/14/NetworkFlow.html
http://mindlee.com/2011/11/19/network-flow/
Flow Problem - HDU 3549
 题意
题意
给定n个点,m条边,求从点1到点n的最大流(模板题)
思路
Edmonds-Karp + 邻接矩阵
// Edmonds-Karp
#include <cstdio>
#include <cstring>
#include <queue>
using namespace std;
const int N = 15 + 15;
const int inf = 0x3f3f3f3f;
int cap[N][N];
int flow[N];
int pre[N];
queue<int> que;
int bfs(int n, int src, int des){
memset(pre, -1, sizeof(pre));
while(!que.empty()) que.pop();
flow[src] = inf;
que.push(src);
while(!que.empty()){
int u = que.front();
que.pop();
for(int v = 1; v <= n; v++){
if(v != src && cap[u][v] > 0 && pre[v] == -1){
flow[v] = min(cap[u][v], flow[u]);
pre[v] = u;
que.push(v);
}
}
}
return pre[des] == -1 ? 0 : flow[des];
}
int solve(int n, int src, int des){
memset(flow, 0, sizeof(flow));
int sum = 0, aug;
while((aug = bfs(n, src, des))){
sum += aug;
for(int v = des, u = pre[des]; v != src; v = u, u = pre[u]){
cap[u][v] -= aug;
cap[v][u] += aug;
}
}
return sum;
}
int main(){
int t, csn = 1;
scanf("%d", &t);
while(t--){
memset(cap[0], 0, sizeof(cap));
int n, m;
scanf("%d%d", &n, &m);
while(m--){
int u, v, val;
scanf("%d%d%d", &u, &v, &val);
cap[u][v] += val;
}
printf("Case %d: %d\n", csn++, solve(n, 1, n));
}
}
Dinic + 邻接表 + 弧优化
// Dinic
#include <cstdio>
#include <cstring>
#include <queue>
using namespace std;
const int N = 15 + 15;
const int M = 1000 + 15;
const int inf = 0x3f3f3f3f;
struct edge{
int v, val, nxt;
};
int dpt[N], head[N], cur[N];
edge e[M << 1];
int tot;
queue<int> que;
inline void init(){
memset(head, -1, sizeof(head));
tot = 0;
}
void addEdge(int u, int v, int val){
e[tot].v = v;
e[tot].val = val;
e[tot].nxt = head[u];
head[u] = tot++;
}
// 在残留网络中分层,即求出点到源点的距离
// 最后如果dpt[des]为0,说明不可分层,不存在增广路
bool getDpt(int src, int des){
while(!que.empty()) que.pop();
memset(dpt, 0, sizeof(dpt));
dpt[src] = 1;
que.push(src);
while(!que.empty()){
int u = que.front();
que.pop();
for(int i = head[u]; ~i; i = e[i].nxt){
int v = e[i].v;
if(e[i].val > 0 && dpt[v] == 0){
dpt[v] = dpt[u] + 1;
que.push(v);
}
}
}
return dpt[des];
}
int dfs(int u, int dist, int src, int des){
if(u == des) return dist;
//cur[u]为弧优化,返回时从下一条边开始搜
for(int& i = cur[u]; ~i; i = e[i].nxt){
int v = e[i].v;
if(dpt[v] == dpt[u] + 1 && e[i].val){
int aug = dfs(v, min(dist, e[i].val), src, des);
if(aug > 0){
e[i].val -= aug;
e[i^1].val += aug;
return aug;
}
}
}
return 0;
}
int Dinic(int src, int des){
int ans = 0;
while(getDpt(src, des)){
int aug;
memcpy(cur, head, sizeof(head));
while((aug = dfs(src, inf, src, des))) ans += aug;
}
return ans;
}
int main(){
int t, csn = 1;
scanf("%d", &t);
while(t--){
init();
int n, m;
scanf("%d%d", &n, &m);
while(m--){
int u, v, val;
scanf("%d%d%d", &u, &v, &val);
addEdge(u, v, val);
addEdge(v, u, 0);
}
printf("Case %d: %d\n", csn++, Dinic(1, n));
}
}
ISAP + 邻接表 + 弧优化 + GAP
// ISAP
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 15 + 15;
const int M = 1e3 + 15;
const int inf = 0x3f3f3f3f;
struct edge{
int v, val, nxt;
};
int d[N], head[N], gap[N], cur[N], pre[N];
edge e[M << 1];
int tot;
inline void init(){
memset(head, -1, sizeof(head));
memset(d, 0, sizeof(d));
memset(gap, 0, sizeof(gap));
tot = 0;
}
void addEdge(int u, int v, int val){
e[tot].v = v;
e[tot].val = val;
e[tot].nxt = head[u];
head[u] = tot++;
}
int ISAP(int n, int src, int des){
memcpy(cur, head, sizeof(head));
int sum = 0;
int u = pre[src] = src;
gap[0] = n;
//当src到des无路径时,d[src]必定会大于或等于n
while(d[src] < n){
//如果u到达des,则增广
if(u == des){
int aug = inf, v;
for(u = pre[des], v = des; v != src; v = u, u = pre[u]) aug = min(aug, e[cur[u]].val);
for(u = pre[des], v = des; v != src; v = u, u = pre[u]){
e[cur[u]].val -= aug;
e[cur[u]^1].val += aug;
}
sum += aug;
continue;
}
//非递归式dfs,寻找可增广路径
bool flag = false;
for(int& i = cur[u]; ~i; i = e[i].nxt){
int v = e[i].v;
if(d[u] == d[v] + 1 && e[i].val){
pre[v] = u;
u = v;
flag = true;
break;
}
}
//若无允许弧,则寻找残留网络中邻接边d最小值,令d[u] = min{...}+1
//更新GAP
//回退到上一个点继续搜
if(!flag){
int mind = n;
for(int i = head[u]; ~i; i = e[i].nxt){
int v = e[i].v;
if(e[i].val && d[v] < mind){
mind = d[v];
cur[u] = i;
}
}
if((--gap[d[u]]) == 0) break;
d[u] = mind + 1;
gap[d[u]]++;
u = pre[u];
}
}
return sum;
}
int main(){
int t, csn = 1;
scanf("%d", &t);
while(t--){
init();
int n, m;
scanf("%d%d", &n, &m);
while(m--){
int u, v, val;
scanf("%d%d%d", &u, &v, &val);
addEdge(u, v, val);
addEdge(v, u, 0);
}
printf("Case %d: %d\n", csn++, ISAP(n, 1, n));
}
}
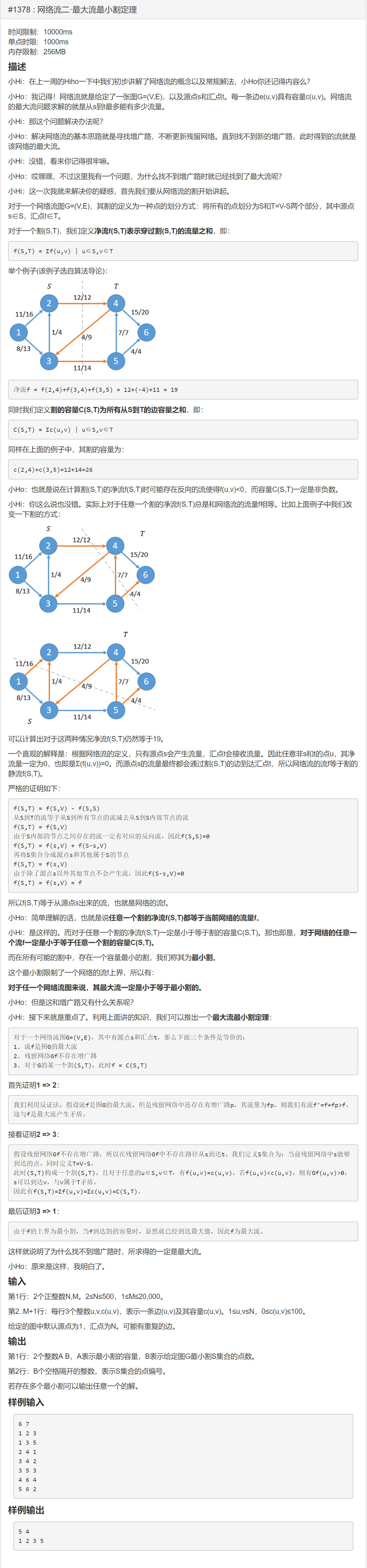
hihoCoder #1378:网络流二·最大流最小割定理
 思路
思路
根据定理1,最大流 = 最小割
根据定理3,跑完最大流后再搜一遍在残留网络中S能连接到的点就ok
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 500 + 15;
const int M = 2e4 + 15;
const int inf = 0x3f3f3f3f;
struct edge{
int v, val, nxt;
};
int d[N], head[N], gap[N], cur[N], pre[N], que[N];
edge e[M << 1];
int tot, qhead, qtail;
inline void init(){
memset(head, -1, sizeof(head));
memset(d, 0, sizeof(d));
memset(gap, 0, sizeof(gap));
tot = 0;
}
void addEdge(int u, int v, int val){
e[tot].v = v;
e[tot].val = val;
e[tot].nxt = head[u];
head[u] = tot++;
}
int ISAP(int n, int src, int des){
memcpy(cur, head, sizeof(head));
int sum = 0;
int u = pre[src] = src;
gap[0] = n;
while(d[src] < n){
if(u == des){
int aug = inf, v;
for(u = pre[des], v = des; v != src; v = u, u = pre[u]) aug = min(aug, e[cur[u]].val);
for(u = pre[des], v = des; v != src; v = u, u = pre[u]){
e[cur[u]].val -= aug;
e[cur[u]^1].val += aug;
}
sum += aug;
continue;
}
bool flag = false;
for(int& i = cur[u]; ~i; i = e[i].nxt){
int v = e[i].v;
if(d[u] == d[v] + 1 && e[i].val){
pre[v] = u;
u = v;
flag = true;
break;
}
}
if(!flag){
int mind = n;
for(int i = head[u]; ~i; i = e[i].nxt){
int v = e[i].v;
if(e[i].val && d[v] < mind){
mind = d[v];
cur[u] = i;
}
}
if((--gap[d[u]]) == 0) break;
d[u] = mind + 1;
gap[d[u]]++;
u = pre[u];
}
}
return sum;
}
int ans[N], pans;
bool used[N];
void getCut(int src){
memset(used, false, sizeof(used));
pans = 0;
qhead = qtail = 0;
que[qtail++] = src;
used[src] = true;
while(qhead != qtail){
int u = que[qhead++];
ans[pans++] = u;
for(int i = head[u]; ~i; i = e[i].nxt){
int v = e[i].v;
if(used[v] || e[i].val == 0) continue;
que[qtail++] = v;
used[v] = true;
}
}
}
int main(){
int n, m;
while(~scanf("%d%d", &n, &m)){
init();
while(m--){
int u, v, val;
scanf("%d%d%d", &u, &v, &val);
addEdge(u, v, val);
addEdge(v, u, 0);
}
int maxn = ISAP(n, 1, n);
getCut(1);
printf("%d %d\n", maxn, pans);
for(int i = 0; i < pans; i++){
printf("%d", ans[i]);
if(i < pans - 1) putchar(' ');
}
puts("");
}
}


