状压搜索、迭代加深搜索、剪枝、记忆化搜索
前言
继续填搜索的坑,不过估计是永远也填不完的 QAQ
- 埃及分数问题 与 迭代加深搜索
https://www.cnblogs.com/hchlqlz-oj-mrj/p/5389223.html - 剪枝
https://hrbust-acm-team.gitbooks.io/acm-book/content/search/search_opt.html
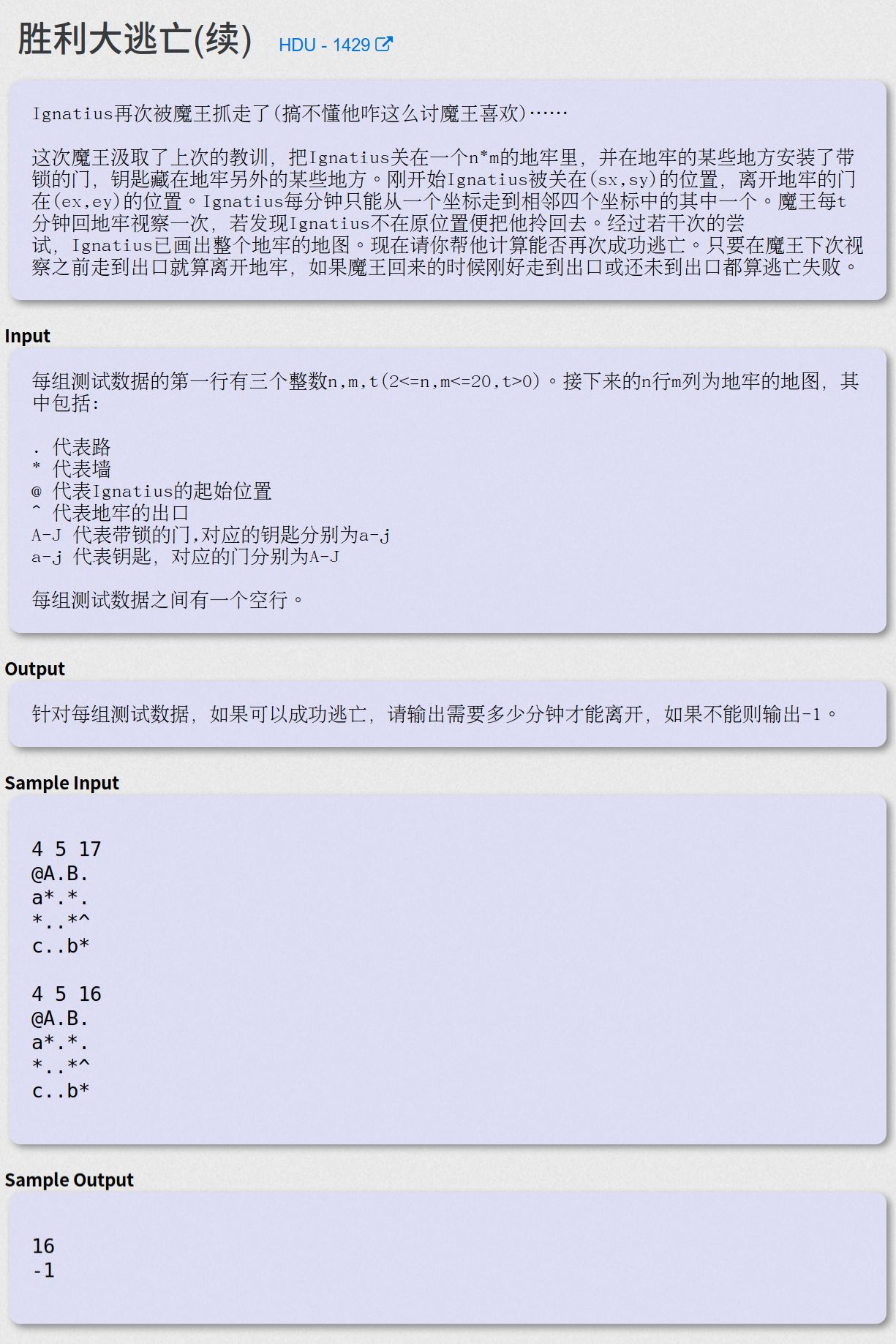
胜利大逃亡(续) - HDU - 1429
思路 —— 状压搜索
这题与普通的搜索题的区别在于有钥匙和锁的门,借助状压DP的思想以及门只有从A到J十个,我们的used数组可以开多一维表示目前在点(x,y)拿到了哪些钥匙,而搜索时使用BFS,也多加一个变量用于表示当前拿到哪些钥匙,再对应搜索即可
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
const int N = 20 + 3;
const int inf = 0x3f3f3f3f;
struct Node{
pii dor;
int step, st;
};
bool used[N][N][1 << 10];
char G[N][N];
const int dx[] = {1, 0, -1, 0};
const int dy[] = {0, 1, 0, -1};
int bfs(pii src, pii des, int n, int m, int k){
memset(used, false, sizeof(used));
queue<Node> que;
que.push(Node{src, 0, 0});
while(!que.empty()){
Node u = que.front();
que.pop();
if(u.step >= k) return inf; //加上这个剪枝会快很多
int x = u.dor.first, y = u.dor.second;
for(int k = 0; k < 4; k++){
int nx = x + dx[k], ny = y + dy[k];
int nst = u.st;
if(nx < 0 || nx >= n || ny < 0 || ny >= m) continue;
if(G[nx][ny] == '*') continue;
//还没拿到这个门的钥匙则不能往里走
if(G[nx][ny] >= 'A' && G[nx][ny] <= 'J' && (u.st & (1 << (G[nx][ny] - 'A'))) == 0) continue;
//拿到新的钥匙则更新状态
if(G[nx][ny] >= 'a' && G[nx][ny] <= 'j') nst |= (1 << (G[nx][ny] - 'a'));
if(used[nx][ny][nst]) continue;
used[nx][ny][nst] = true;
if(make_pair(nx, ny) == des) return u.step + 1;
que.push(Node{make_pair(nx, ny), u.step + 1, nst});
}
}
return inf;
}
int main(){
int n, m, k;
while(~scanf("%d%d%d", &n, &m, &k)){
for(int i = 0; i < n; i++) scanf("%s", G[i]);
pii src, des;
for(int i = 0; i < n; i++){
for(int j = 0; j < m; j++){
if(G[i][j] == '@') src = make_pair(i, j);
if(G[i][j] == '^') des = make_pair(i, j);
}
}
int ans = bfs(src, des, n, m, k);
printf("%d\n", ans < k ? ans : -1);
}
}
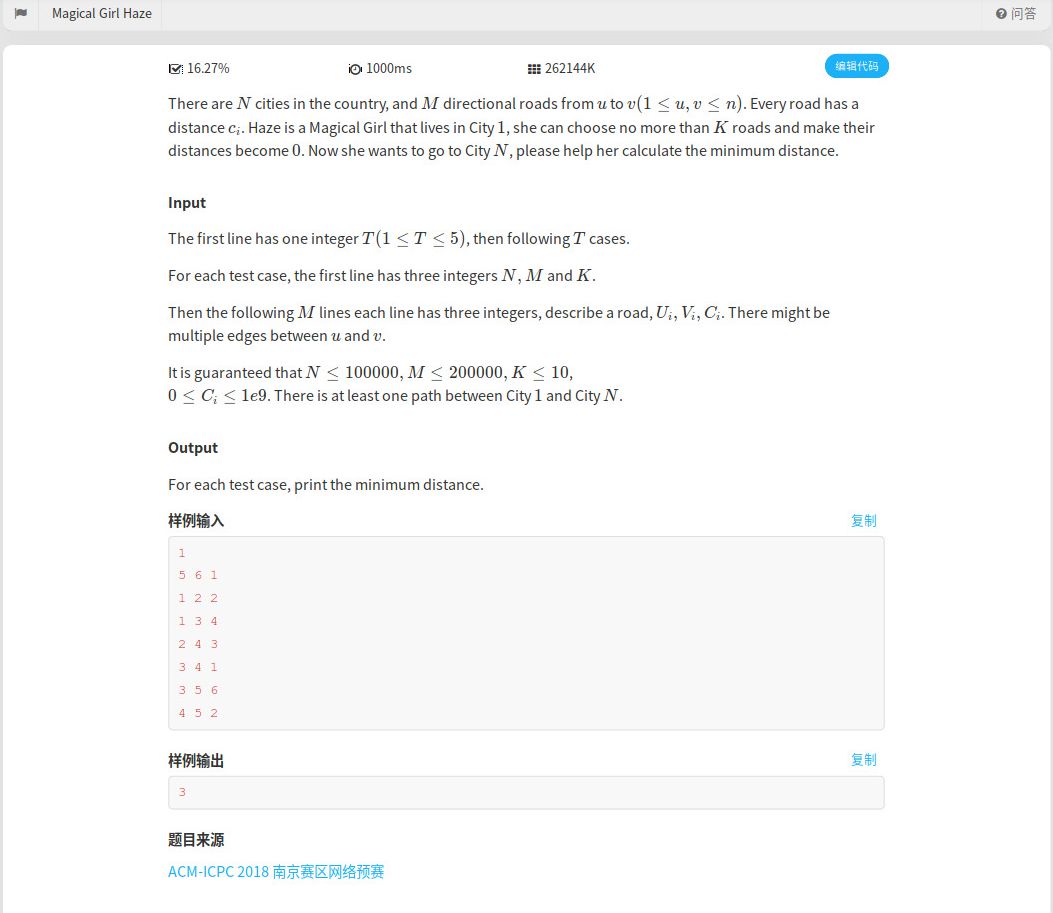
Magical Girl Haze - ACM-ICPC 2018 南京赛区网络预赛
题意
给定一幅图,求将K条边置为0后,从点1到点n的最短路的值
思路 —— 最短路 + 状压思想
借助状压DP的思想,在跑Dijkstra的时候在d数组上多开一维记录下在删除k条边时到达这一点的最短路的值,队列中也是多开一维记录下当前已经删除了k条边,再进入进入下一个点时,可以不删边进入,在当前还能继续删边时,还要再加入一个删边进入了的点
另外,在队列中让删边多的点先出队列能提高运行效率(不确定不这样做会不会TLE)
最后,答案是d[n][k]
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
const int N = 1e5 + 3;
const int M = 2e5 + 3;
const ll inf = 1LL << 60;
struct edge{
int v, w, nxt;
};
struct Node{
int u;
ll w;
int k;
bool operator < (const Node& b) const{
if(w != b.w) return w > b.w;
else return k < b.k;
}
};
priority_queue<Node> que;
ll d[N][12];
edge e[M];
int head[N];
int tot;
inline int read(){
char ch = getchar(); int x = 0, f = 1;
while(ch < '0' || ch > '9') {if(ch == '-') f = -1; ch = getchar();}
while('0' <= ch && ch <= '9') {x = x * 10 + ch - '0'; ch = getchar();}
return x * f;
}
inline void init(){
memset(head, -1, sizeof(head));
tot = 0;
}
inline void addEdge(int u, int v, int w){
e[tot] = edge{v, w, head[u]};
head[u] = tot++;
}
ll dijkstra(int n, int lim){
while(!que.empty()) que.pop();
fill(d[0], d[N - 1] + 12, inf);
d[1][0] = 0;
que.push(Node{1, 0, 0});
while(!que.empty()){
Node nd = que.top();
que.pop();
int u = nd.u, w = nd.w, k = nd.k;
if(w > d[u][k]) continue;
if(u == n) return w;
for(int i = head[u]; ~i; i = e[i].nxt){
int v = e[i].v;
if(d[v][k] > d[u][k] + e[i].w){
d[v][k] = d[u][k] + e[i].w;
que.push(Node{v, d[v][k], k});
}
if(k + 1 <= lim && d[v][k + 1] > d[u][k]){
d[v][k + 1] = d[u][k];
que.push(Node{v, d[v][k + 1], k + 1});
}
}
}
return inf;
}
int main(){
int t = read();
while(t--){
int n = read(), m = read(), k = read();
init();
while(m--){
int u = read(), v = read(), w = read();
addEdge(u, v, w);
}
printf("%lld\n", dijkstra(n, k));
}
}
埃及分数 - Vijos 1308
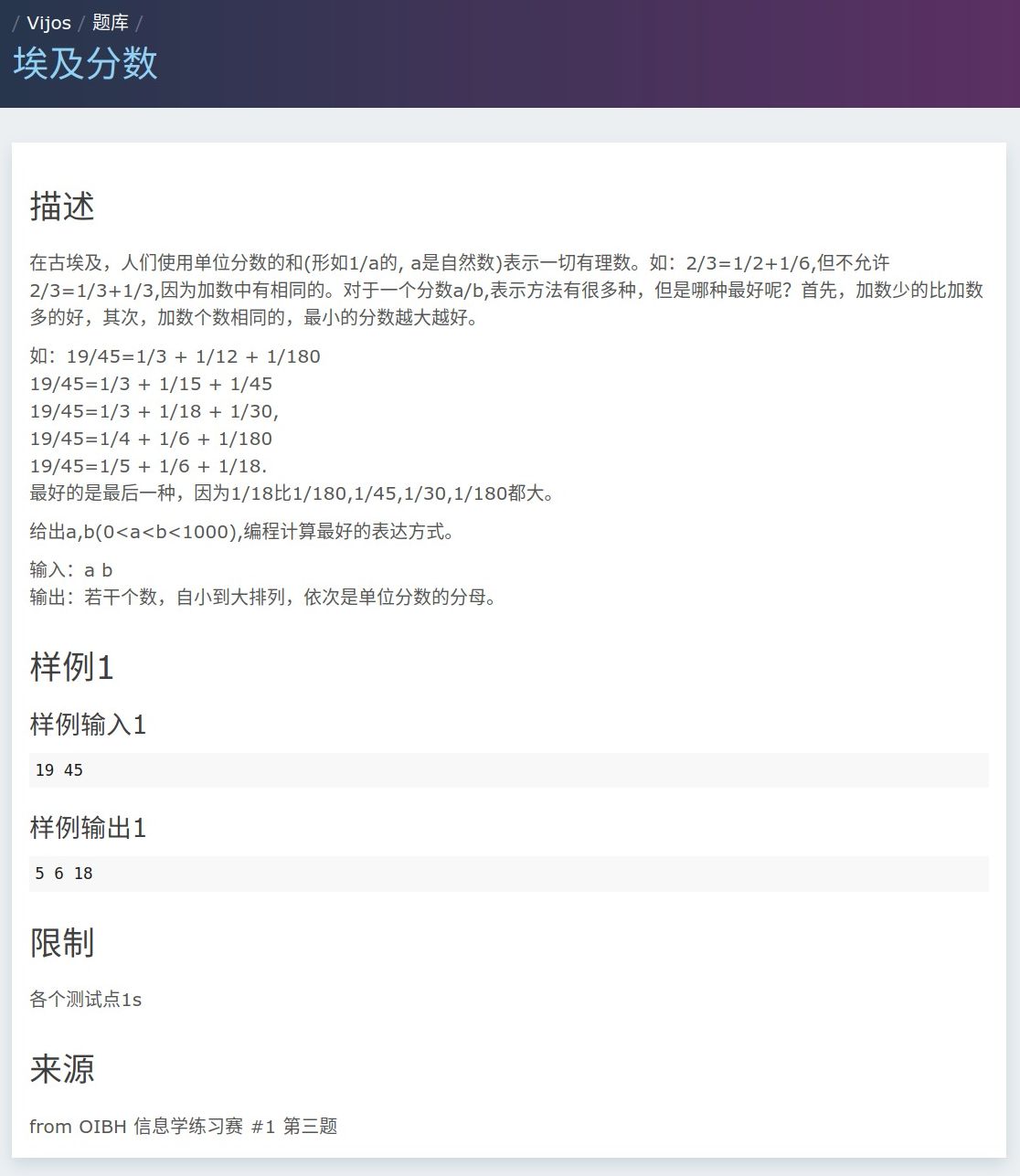
思路 —— 迭代加深搜索
具体见上面的博客链接,蒟蒻觉得那个写得蛮好的
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
typedef long long ll;
const int N = 20;
const double eps = 1e-6;
ll ans[N], tmp[N] = {0};
bool dfs(int i, int lim, ll a, ll b){
if(i > lim){
if(a == 0 && ans[lim] > tmp[lim]) memcpy(ans, tmp, sizeof(tmp));
return a == 0;
}
ll l = max(b/a, tmp[i - 1] + 1), r = b/a*(lim - i + 1);
bool flag = false;
for(ll j = l; j <= r; j++){
ll nb = b*j/__gcd(b, j);
ll na = a*nb/b - nb/j;
if(na < 0) continue;
tmp[i] = j;
if(dfs(i + 1, lim, na, nb)) flag = true;
}
return flag;
}
int main(){
ll a, b;
while(~scanf("%lld%lld", &a, &b) && (a | b)){
memset(ans, 0x3f, sizeof(ans));
int lim = 1;
while(!dfs(1, lim, a, b)) lim++;
for(int i = 1; i <= lim; i++){
printf("%lld", ans[i]);
if(i < lim) putchar(' ');
}
puts("");
}
}
Addition Chains - POJ - 2248
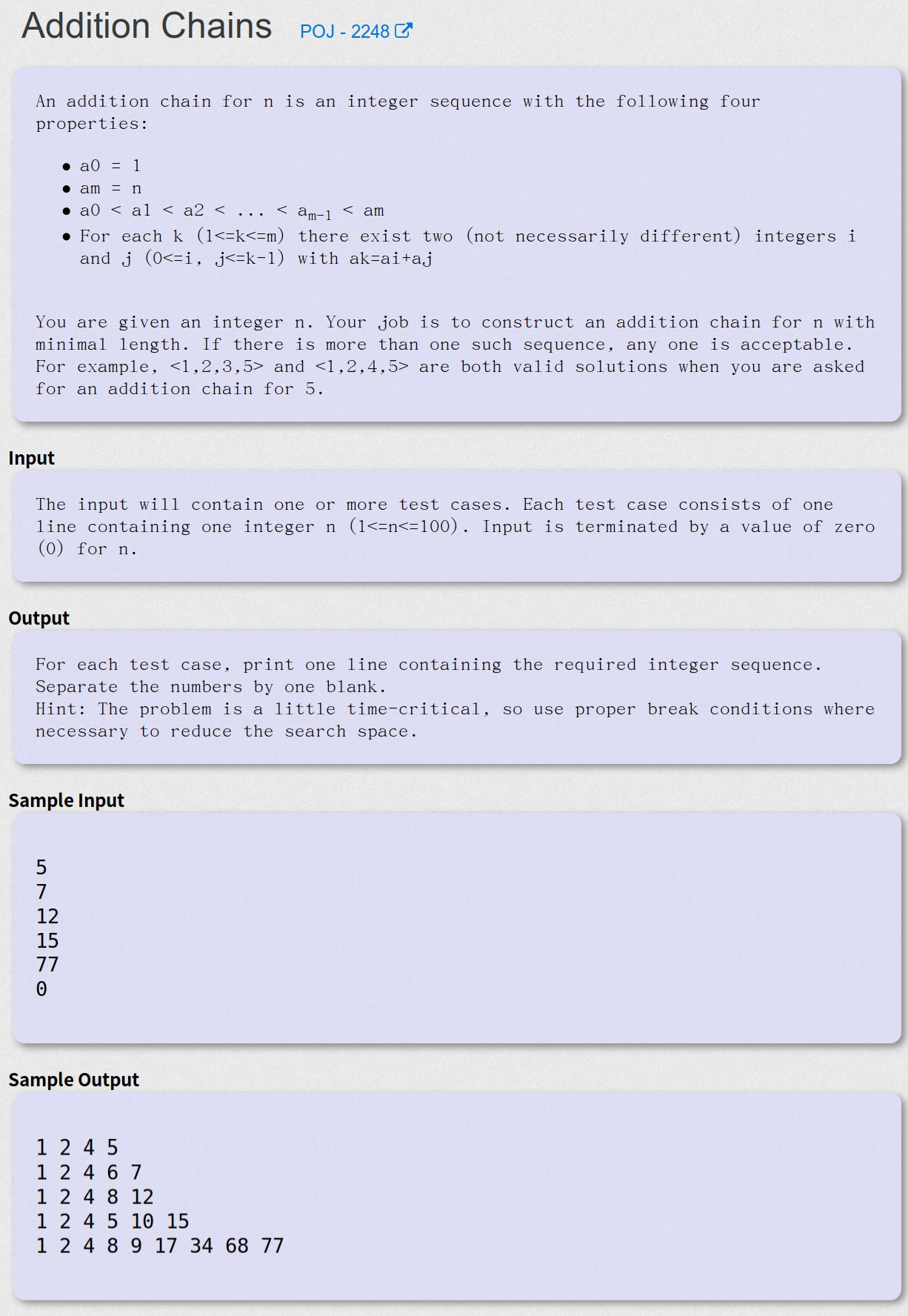
题意
给定一个数n,求一个严格递增的序列满足1, .., n,,且对于任意一个(1 <= k <= m)上的数ak,都存在ak = ai + aj(除了开头的1不需要满足),且序列元素个数需满足最小
思路 —— 迭代加深搜索
考虑使用迭代加深搜索,逐层递增进行搜索
每次算一个数,同时要用打表思维打出下一个数有哪些数是可以填的
最后就是普通的搜索
#include <iostream>
#include <cstring>
#include <cstdio>
#include <vector>
#include <map>
#include <set>
#include <algorithm>
using namespace std;
typedef long long ll;
const int N = 200 + 15;
int cnt[N] = {0, 1};
int tmp[N] = {1}, ans[N] = {1};
bool dfs(int i, int lim, int m){
if(i > lim){
memcpy(ans, tmp, sizeof(tmp));
return true;
}
int l, r;
if(i == 1) l = r = 1;
else if(i == lim) l = max(m, tmp[i - 1] + 1), r = m;
else l = tmp[i - 1] + 1, r = m - 1;
bool flag = false;
for(int x = l; x <= r; x++){
if(!cnt[x]) continue;
tmp[i] = x;
for(int j = i; j >= 1; j--){
cnt[x + tmp[j]]++;
}
if(dfs(i + 1, lim, m)) flag = true;
for(int j = i; j >= 1; j--){
cnt[x + tmp[j]]--;
}
if(flag) return true;
}
return flag;
}
int main() {
int m;
while(scanf("%d", &m) && m){
if(m == 1){
puts("1");
}else{
int n = 2;
while(!dfs(1, n, m)) n++;
for(int i = 1; i <= n; i++){
printf("%d", ans[i]);
if(i < n) putchar(' ');
}
puts("");
}
}
return 0;
}
N皇后问题 - HDU - 2553
思路 —— 状压搜索
其实用状压DP的思路迁移一下就可以了
具体见代码
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
typedef long long ll;
const int N = 20;
const double eps = 1e-6;
int a[N];
//ld:y=x的对角线不可放位置
//m:x=0的线不可放的位置
//rd:y=-x的对角线不可放的位置
int dfs(int dpt, int n, int ld, int m, int rd){
if(dpt > n) return 1;
int st = ~(ld | m | rd); //取反,得到可放的位置
if(!st) return 0;
int ans = 0;
for(int cur = (1 << (n - 1)), j = 1; cur >= 1; cur >>= 1, j++){
if((st & cur) == 0) continue; //当前位置不可放,则continue
//更新ld,m,rd的信息
ans += dfs(dpt + 1, n, (ld | cur) << 1, m | cur, (rd | cur) >> 1);
}
return ans;
}
int main(){
for(int i = 1; i <= 10; i++) a[i] = dfs(1, i, 0, 0, 0);
int n;
while(scanf("%d", &n) && n){
printf("%d\n", a[n]);
}
}
Tempter of the Bone - ZOJ - 2110
题意
给定一个迷宫,走过的路不能再走,问是否能在t时刻到达出口
思路 —— 奇偶剪枝
实际上只是普通的DFS加上奇偶剪枝
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
const int N = 10;
const int dx[] = {1, 0, -1, 0};
const int dy[] = {0, 1, 0, -1};
char G[N][N];
bool used[N][N];
inline int mabs(int x){ return x > 0 ? x : -x; }
inline int getDistance(const pii& u, const pii& v){
return mabs(u.first - v.first) + mabs(u.second - v.second);
}
bool dfs(pii u, pii des, int step, int lim, int n, int m){
if(u == des) return step == lim;
int x = u.first, y = u.second, d = getDistance(u, des);
//当前步数 + 到des的最短距离还比lim大,那么肯定到不了,剪枝
if(step + d > lim) return false;
//lim - step与d的奇偶性不同,即剩下要走的步数和最短步数奇偶性不同
//根据奇偶剪枝,肯定走不到,减掉
if((lim - step - d)&1) return false;
for(int k = 0; k < 4; k++){
int nx = x + dx[k], ny = y + dy[k];
if(nx < 0 || nx >= n || ny < 0 || ny >= m) continue;
if(G[nx][ny] == 'X' || used[nx][ny]) continue;
used[nx][ny] = true;
if(dfs(make_pair(nx, ny), des, step + 1, lim, n, m)) return true;
used[nx][ny] = false;
}
return false;
}
int main(){
int n, m, k;
while(~scanf("%d%d%d", &n, &m, &k) && (n | m | k)){
for(int i = 0; i < n; i++) scanf("%s", G[i]);
pii src, des;
for(int i = 0; i < n; i++){
for(int j = 0; j < m; j++){
if(G[i][j] == 'S'){
src = make_pair(i, j);
}else if(G[i][j] == 'D'){
des = make_pair(i, j);
}
}
}
memset(used, false, sizeof(used));
used[src.first][src.second] = true;
puts(dfs(src, des, 0, k, n, m) ? "YES" : "NO");
}
}
Free Candies - UVA - 10118

题意
给定4堆糖果,每堆n个,每次能从某一堆的顶部拿一个糖果放入容量为5的背包中,若背包中有两个糖果种类相同,则可消除那两个糖果并加1分,问总最大得分
思路 —— 记忆化搜索
4堆糖果各自剩余的数量若固定,则在此状态下能拿到的最大分数也是固定的
因为假设已达到这样一个状态,则不管如何达到这样一个状态,背包中的糖果一定是相同的(顺序可能不同),毕竟能消除的已经消除了,才能达到这样一个状态
那么就记录这个状态的值,做记忆化搜索即可
#include <iostream>
#include <cstdio>
#include <map>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 40 + 1;
int arr[4][N], ptr[4] = {0};
int dp[N][N][N][N];
int cnt[N];
inline void init(){
memset(dp, -1, sizeof(dp));
memset(cnt, 0, sizeof(cnt));
}
int dfs(int p, int n){
if(p >= 5) return 0;
if(dp[ptr[0]][ptr[1]][ptr[2]][ptr[3]] != -1) return dp[ptr[0]][ptr[1]][ptr[2]][ptr[3]];
int ans = 0;
for(int i = 0; i < 4; i++){
if(ptr[i] >= n) continue;
int val = arr[i][ptr[i]];
ptr[i]++;
cnt[val]++;
if(cnt[val] >= 2){
cnt[val] = 0;
ans = max(ans, dfs(p - 1, n) + 1);
cnt[val] = 2;
}else{
ans = max(ans, dfs(p + 1, n));
}
cnt[val]--;
ptr[i]--;
}
dp[ptr[0]][ptr[1]][ptr[2]][ptr[3]] = ans;
return ans;
}
int main(){
int n;
while(~scanf("%d", &n) && n){
init();
for(int j = 0; j < n; j++){
for(int i = 0; i < 4; i++){
scanf("%d", &arr[i][j]);
}
}
printf("%d\n", dfs(0, n));
}
}


