欧拉路、Fleury算法、有向图的欧拉路
前言
会欧拉路之后基本上能秒杀一笔画问题 ヾ(o◕∀◕)ノヾ
参考资料蒟蒻建议是HihoCoder的欧拉路三题
欧拉路·一 - HihoCoder - 1176
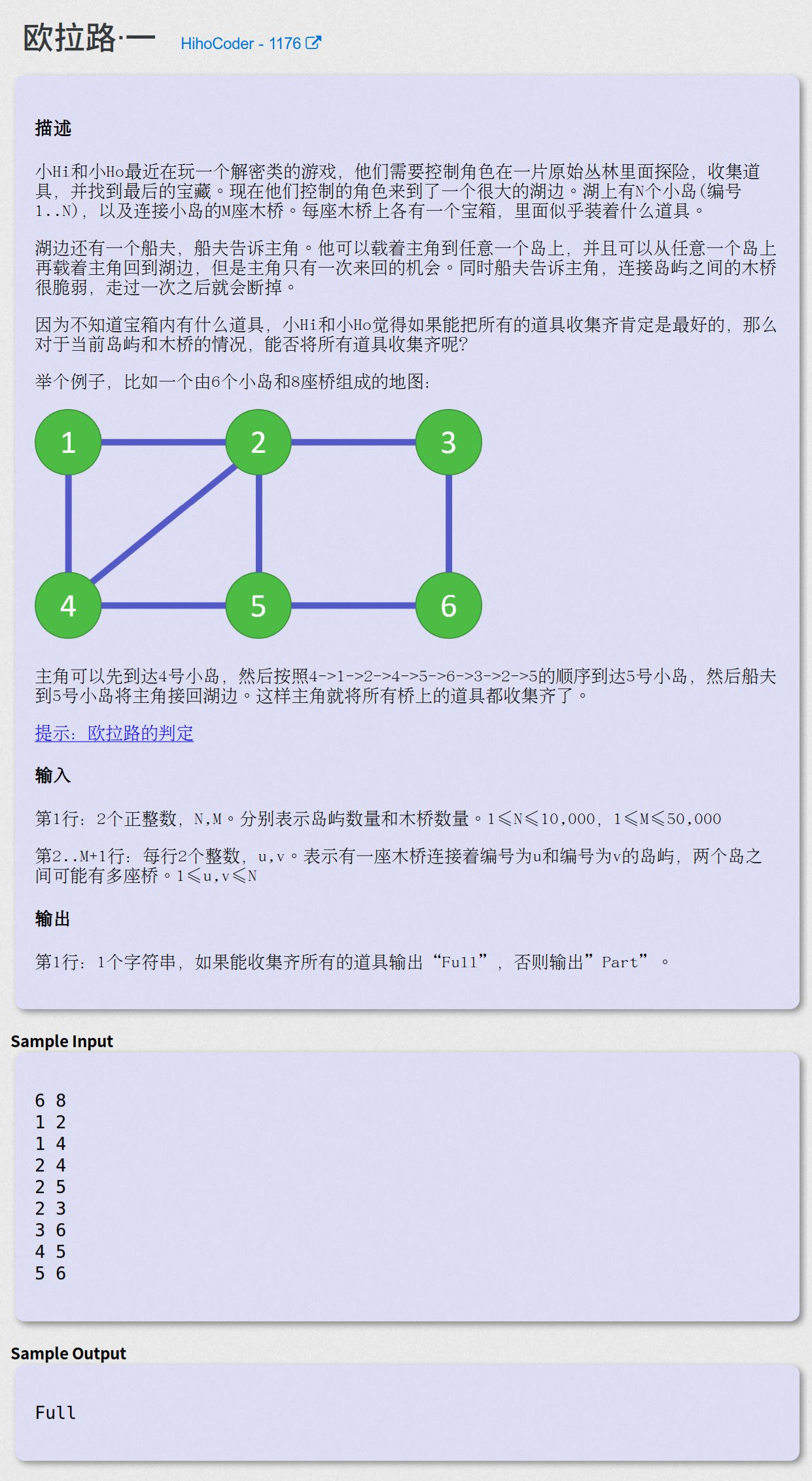
思路 —— 欧拉路存在的判定
不需要真的加边,只需要判断每个点的度数,度数为奇数的点的个数为0或2即可
#include <iostream>
#include <cstdio>
#include <map>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1e4 + 5;
const int M = 5e4 + 5;
typedef long long ll;
int dg[N];
inline void init(){
memset(dg, 0, sizeof(dg));
}
bool judge(int n){
int cnt = 0;
for(int i = 1; i <= n; i++){
if(dg[i]&1) cnt++;
}
return (cnt == 0 || cnt == 2);
}
int main(){
int n, m;
while(~scanf("%d%d", &n, &m)){
while(m--){
int u, v;
scanf("%d%d", &u, &v);
dg[v]++;
dg[u]++;
}
puts(judge(n) ? "Full" : "Part");
}
}
欧拉路·二 - HihoCoder - 1181

思路 —— Fleury算法找欧拉路
Fleury算法模板题
#include <iostream>
#include <cstdio>
#include <map>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1e3 + 5;
const int M = 5e3 + 5;
typedef long long ll;
struct edge{
int v, nxt;
};
edge e[M << 1];
int head[N], tot, dg[N];
int ans[M << 1], pp;
bool used[M << 1];
inline void init(){
memset(dg, 0, sizeof(dg));
memset(head, -1, sizeof(head));
memset(used, false, sizeof(used));
tot = 0, pp = 0;
}
inline void addEdge(int u, int v){
e[tot] = edge{v, head[u]};
head[u] = tot++;
dg[v]++;
}
int getSrc(int n){
for(int i = 1; i <= n; i++){
if(dg[i]&1){
return i;
}
}
return 1;
}
void dfs(int u){
for(int i = head[u]; ~i; i = e[i].nxt){
int v = e[i].v;
if(used[i]) continue;
used[i] = used[i^1] = true;
dfs(v);
}
ans[pp++] = u;
}
int main(){
int n, m;
while(~scanf("%d%d", &n, &m)){
init();
while(m--){
int u, v;
scanf("%d%d", &u, &v);
addEdge(u, v);
addEdge(v, u);
}
dfs(getSrc(n));
for(int i = 0; i < pp; i++){
printf("%d", ans[i]);
if(i < pp - 1) putchar(' ');
}
puts("");
}
}
The Best Path - HDU - 5883
题意
给定一幅连通图,问是否存在一条路径能经过每条边正好一次,能的话求出经过的点权值异或最大值(按重数计)
思路
首先明显是欧拉路
先判断是否存在欧拉路,再判断是否为欧拉回路
若非欧拉回路,则权值最大值只能是经过的路径上的点的异或值
若是欧拉回路,则因为起点也是终点,会经过两次所以异或值不计,路径的异或值就是除起点外经过的点的异或值
最后一个问题是,如何才能知道一个点经过了几次?这与度数相关,要形成欧拉路,除了起点和终点,其他点必定入度=出度,因此 度数/2 就是经过的次数,而起点和终点如果不是同一个点,则是 (度数 + 1)/2,如果是同一个点,因为一进一出,因此也是 (度数 + 1)/2
现在要取得最大值,对于非欧拉回来直接算经过奇数次的点的异或值即可,对于欧拉回路则在原来的基础上枚举起点,最终结果再异或a[i]即可(原来经过奇数次,现在会经过偶数次,反之则相反)
#include <iostream>
#include <cstdio>
#include <map>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 100000 + 5;
typedef long long ll;
int a[N], dg[N];
int main(){
int t;
scanf("%d", &t);
while(t--){
memset(dg, 0, sizeof(dg));
int n, m;
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i++){
scanf("%d", &a[i]);
}
while(m--){
int u, v;
scanf("%d%d", &u, &v);
dg[u]++;
dg[v]++;
}
int cnt = 0, xorsum = 0;
for(int i = 1; i <= n; i++){
if(dg[i]&1) cnt++;
if(((dg[i] + 1) >> 1)&1) xorsum ^= a[i];
}
if(cnt != 0 && cnt != 2) puts("Impossible");
else if(cnt == 2){
printf("%d\n", xorsum);
}else{
int ans = xorsum ^ a[1];
for(int i = 2; i <= n; i++){
ans = max(ans, xorsum ^ a[i]);
}
printf("%d\n", ans);
}
}
}
Catenyms - POJ - 2337
题意
给定一些字符串,问能否恰巧用每个字符串一次,组成一个当前首字母与上一个字符串尾字母相同,当前尾字母与下一个字符串首字母相同的字符串(要求字典序最小)
思路 —— 有向图的欧拉路
以首位字母为点,当前字符串为边建图,那么要求的字符串就是欧拉路形成的字符串
本题要求字典序最小,因此加边前先按字典序降序排序,然后再加边,因为邻接表实际上是逆序加入的,所以到时候遍历是正序,即字典序逐渐增加的顺序
另外题目不保证图连通,因此还要注意检查答案是否是所有的边
最后注意是有向图,因此要逆序输出
#include <iostream>
#include <cstdio>
#include <map>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1000 + 5;
const int M = 27;
typedef long long ll;
struct edge{
int v, w, next;
};
char tmps[M];
string s[N];
edge e[N];
int head[M];
int tot;
int in[M], out[M];
int ans[N << 1], pp;
bool used[N];
inline int mabs(int x){ return x > 0 ? x : -x; }
inline void init(){
pp = tot = 0;
memset(head, -1, sizeof(head));
memset(used, false, sizeof(used));
memset(in, 0, sizeof(in));
memset(out, 0, sizeof(out));
}
inline void addEdge(int u, int v, int idx){
e[tot] = edge{v, idx, head[u]};
head[u] = tot++;
out[u]++;
in[v]++;
}
int getSrc(int minsrc){
int cnt1 = 0, cnt2 = 0;
int src = minsrc;
for(int i = 0; i < M; i++){
if(mabs(in[i] - out[i]) > 1) return -1;
if(in[i] == out[i] + 1) {cnt1++;}
if(in[i] == out[i] - 1) {cnt2++; src = i;}
}
if((!cnt1 && !cnt2) || (cnt1 == 1 && cnt2 == 1)){
return src;
}else{
return -1;
}
}
void dfs(int u){
for(int i = head[u]; ~i; i = e[i].next){
if(used[i]) continue;
used[i] = true;
dfs(e[i].v);
ans[pp++] = e[i].w;
}
}
int main(){
int t;
scanf("%d", &t);
while(t--){
init();
int n;
scanf("%d", &n);
for(int i = 0; i < n; i++){
scanf("%s", tmps);
s[i] = string(tmps);
}
sort(s, s + n, greater<string>());
int src = 100;
for(int i = 0; i < n; i++){
addEdge(s[i][0] - 'a', s[i][s[i].size() - 1] - 'a', i);
src = min(src, s[i][0] - 'a');
}
src = getSrc(src);
if(src == -1) puts("***");
else{
dfs(src);
if(pp < n || pp < 3) puts("***");
else{
for(int i = pp - 1; i >= 0; i--){
printf("%s", s[ans[i]].c_str());
if(i > 0) putchar('.');
}
puts("");
}
}
}
}
Tanya and Password - CodeForces - 508D
题意
从一个字符串给出所有连续三位的子区间的字符串,求原字符串
思路 —— 状压搜索
以每个字符串前两位和后两位为点,该字符串为边建图
剩下与上题一样
另外,本题卡递归式的DFS,要用非递归的 QAQ
#include <iostream>
#include <cstdio>
#include <stack>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
const int M = 2e5 + 5;
const int N = 128*128 + 5;
typedef long long ll;
struct edge{
int v, w, nxt;
};
edge e[M];
int head[N], in[N], out[N], tot, pre[M];
bool used[M];
int ans[M], pp;
char s[M];
inline void init(){
memset(used, false, sizeof(used));
memset(head, -1, sizeof(head));
memset(in, 0, sizeof(in));
memset(out, 0, sizeof(out));
tot = pp = 0;
}
inline void addEdge(int u, int v, int idx){
e[tot] = edge{v, idx, head[u]};
head[u] = tot++;
in[v]++;
out[u]++;
}
int getSrc(int minsrc){
int cnt1 = 0, cnt2 = 0;
int src = minsrc;
for(int i = 0; i < N; i++){
if(in[i] == out[i] + 1) {cnt1++;}
else if(in[i] == out[i] - 1) {cnt2++; src = i;}
else if(in[i] != out[i]) return -1;
}
if((!cnt1 && !cnt2) || (cnt1 == 1 && cnt2 == 1)){
return src;
}else{
return -1;
}
}
void dfs(int src){
stack<int> stk, estk;
stk.push(src);
while(!stk.empty()){
int u = stk.top();
bool flag = true;
for(int& i = head[u]; ~i; i = e[i].nxt){
if(used[i]) continue;
used[i] = true;
flag = false;
int v = e[i].v;
stk.push(v);
estk.push(i);
break;
}
if(flag){
if(!estk.empty()){
ans[pp++] = estk.top();
estk.pop();
}
stk.pop();
}
}
}
int main(){
int n;
while(~scanf("%d", &n)){
init();
int src;
for(int i = 0; i < n; i++){
scanf("%s", s);
addEdge(s[0]*128 + s[1], s[1]*128 + s[2], i);
src = s[0] * 128 + s[1];
}
src = getSrc(src);
if(src != -1) dfs(src);
if(src == -1 || pp < n){
puts("NO");
}else{
puts("YES");
printf("%c%c", src/128, src%128);
for(int i = pp - 1; i >= 0; i--){
putchar(e[ans[i]].v%128);
}
puts("");
}
}
}


