刷题记（最近公共祖先（LCA）） —— 2018.9.7

UPDATE: 2019.05.13
· 修改RMQ做法的代码
CONTENT: LCA的RMQ算法、Tarjan算法、倍增算法

Update (2019.05.13)

修改RMQ做法的代码

BB (2019.05.13)

昨天GDCPC剩两个钟的时候和jjdl说你要是把I题A掉了，我就发pyq和说说通报表扬jjdl
不过蒟蒻觉得公号也应该通报表扬！jjdl niubility！！（破音）

BB

LCA是寒假集训的内容，当时一脸懵逼，现在好多了！

Introduction

LCA为最近公共祖先，有倍增、RMQ、Tarjan三种解法

LCA
https://blog.csdn.net/my_sunshine26/article/details/72717112
LCA —— 倍增
https://zhyack.github.io/posts/2015_12_22_LCA-Binary-Lifting-Note.html
LCA —— RMQ
https://www.cnblogs.com/549294286/p/3783423.html

关于对倍增算法的理解

倍增算法是个神奇的东西
首先用一次DFS，将所有点的深度找出来，以及所以点的父亲fa[u][0]找出来
然后初始化fa数组，此时fa数组代表的是u节点往上走 2^j 步是谁，那么可以用DP推出fa数组，即fa[u][j] = fa[fa[u][j - 1]][j - 1] 最后是找LCA，对于给定的点u和v，首先尝试将其跳到同一深度，只需要往下枚举j，一直跳 2^j 步，整个过程满足dpt[v] > dpt[u]即可，此时如果u和v是相同的，那么LCA就是u，如果不同，就两个节点接着一起跳 2^j 步，整个过程满足fa[u][j] != fa[v][j]即可，最后他们的LCA是fa[u][0]
为什么这样做是正确的呢？对于第一个使u和v达到同一深度的过程，假设需要跳x步，我们知道任何一个数都可以用二进制数表示，假设其为11101011，那么往下枚举j的过程实际就是不断从高位往低位消除1的过程，如果该位为1。自然是能跳的，如果为0，则减去 2^j 会变成负数，也就是跳过头，具体体现在dpt[v] <= dpt[u]，而对于第二个过程同理
蒟蒻感觉整个倍增算法充满了DP的味道，所以很多需要DP结合LCA的东西可以直接在倍增算法上面改

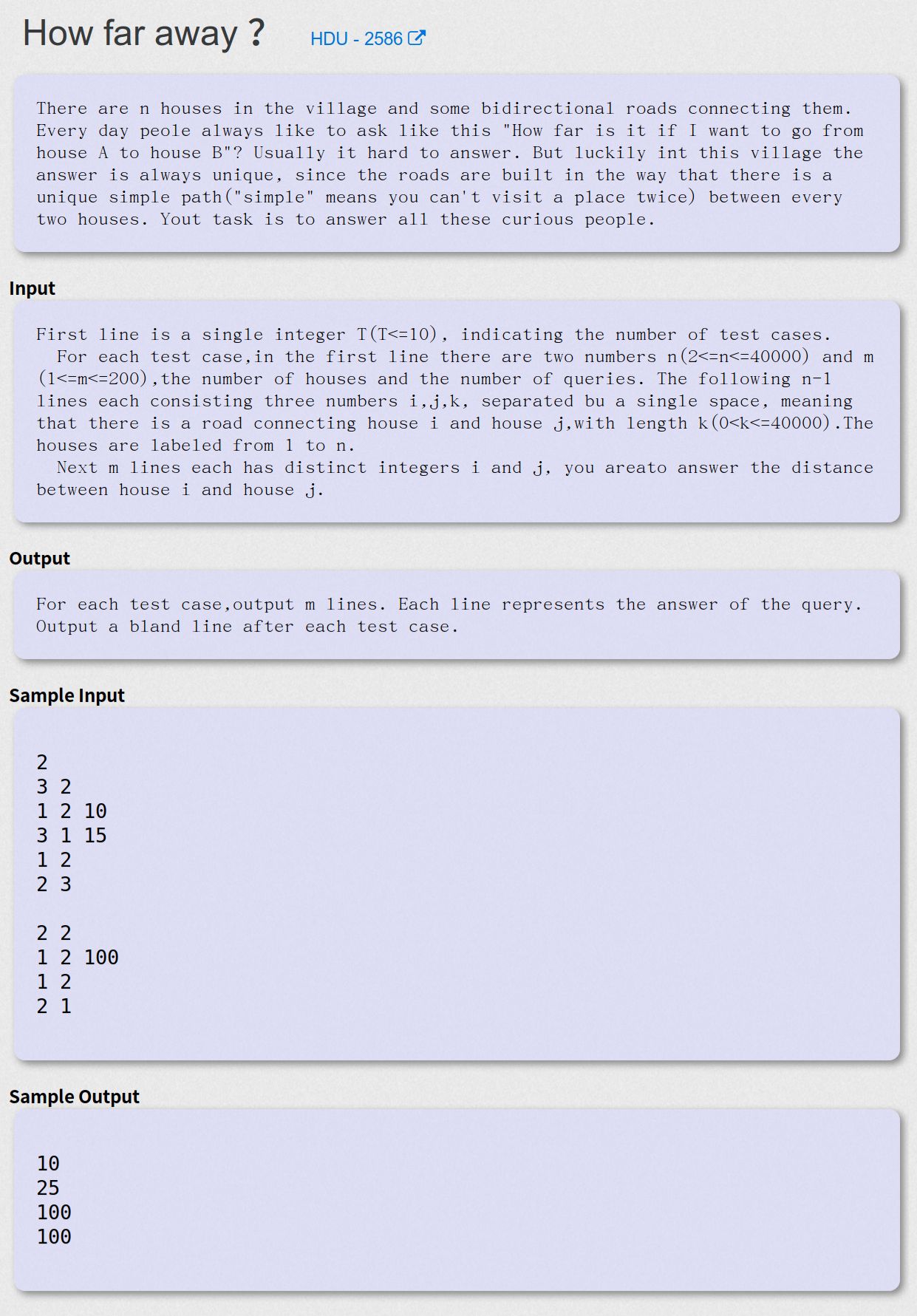
How far away ？ - HDU - 2586

题意
给定一颗树，多次询问点u和v的距离
思路 —— 倍增做法
LCA模板题
u和v的距离也就是 d[u] + d[v] - 2*d[lca(u, v)]，直接默认点1为根即可

#include <iostream>
#include <cstdio>
#include <stack>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
const int N = 40000 + 5;
const int BASE = 16;
typedef long long ll;

struct edge{
    int v, w, nxt;
};
edge e[N << 1];
int  head[N], tot;
int  fa[N][17], dpt[N], d[N];

inline void init(){
    memset(head, -1, sizeof(head));
    memset(fa, -1, sizeof(fa));
    dpt[1] = 0, d[1] = 0;
    tot = 0;
}

inline void addEdge(int u, int v, int w){
    e[tot] = edge{v, w, head[u]};
    head[u] = tot++;
}

void dfs(int u, int pre){
    for(int i = head[u]; ~i; i = e[i].nxt){
        int v = e[i].v;
        if(v == pre)    continue;
        dpt[v] = d[u] + 1;
        d[v] = d[u] + e[i].w;
        fa[v][0] = u;
        dfs(v, u);
    }
}

void getFa(int n){
    for(int j = 1; j <= BASE; j++){
        for(int i = 1; i <= n; i++){

            if(fa[i][j - 1] == -1)  continue;
            fa[i][j] = fa[fa[i][j - 1]][j - 1];
        }
    }
}

int getLca(int u, int v){
    if(dpt[u] > dpt[v])     swap(u, v);
    for(int j = BASE; j >= 0; j--){
        if(fa[v][j] == -1 || dpt[fa[v][j]] < dpt[u])    continue;
        v = fa[v][j];
    }
    if(u == v)  return u;
    for(int j = BASE; j >= 0; j--){
        if(fa[u][j] == -1 || fa[v][j] == -1 || fa[u][j] == fa[v][j])    continue;
        u = fa[u][j], v = fa[v][j];
    }
    return fa[u][0];
}

int main(){
    int t;
    scanf("%d", &t);
    while(t--){
        init();
        int n, m;
        scanf("%d%d", &n, &m);
        for(int i = 1; i <= n - 1; i++){
            int u, v, w;
            scanf("%d%d%d", &u, &v, &w);
            addEdge(u, v, w);
            addEdge(v, u, w);
        }
        dfs(1, -1);
        getFa(n);

        while(m--){
            int u, v;
            scanf("%d%d", &u, &v);
            printf("%d\n", d[u] + d[v] - 2*d[getLca(u, v)]);
        }
    }
}

思路 —— Tarjan做法

#include <iostream>
#include <cstdio>
#include <map>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 40000 + 5;
const int M = 200 + 5;
typedef long long ll;

struct edge{
    int v, w, nxt;
};
edge e[N << 1];
int  head[N], tot, d[N], used[N];
int  ft[N];
edge qe[M << 1];
int  qhead[N], qtot;
int  pa[N];

inline void init(){
    for(int i = 1; i < N; i++)  ft[i] = i;
    memset(head, -1, sizeof(head));
    memset(qhead, -1, sizeof(qhead));
    memset(used, false, sizeof(used));
    d[1] = 0;
    tot = 0;
    qtot = 0;
}

inline void addEdge(int u, int v, int w){
    e[tot] = edge{v, w, head[u]};
    head[u] = tot++;
}

inline void addQ(int u, int v, int i){
    qe[qtot] = edge{v, i, qhead[u]};
    qhead[u] = qtot++;
}

int find(int x){ return ft[x] == x ? x : ft[x] = find(ft[x]); }
void merge(int x, int y){
    int p = find(x), q = find(y);
    if(p != q)  ft[q] = p;
}

void tarjan(int u, int pre, int q){
    for(int i = head[u]; ~i; i = e[i].nxt){
        int v = e[i].v;
        if(v == pre)    continue;
        d[v] = d[u] + e[i].w;
        tarjan(v, u, q);
        merge(u, v);
        used[v] = true;
    }
    for(int i = qhead[u]; ~i; i = qe[i].nxt){
        int v = qe[i].v;
        if(used[v])     pa[qe[i].w] = find(v);
    }
}

int main(){
    int t;
    scanf("%d", &t);
    while(t--){
        init();
        int n, q;
        scanf("%d%d", &n, &q);
        for(int i = 1; i <= n - 1; i++){
            int u, v, w;
            scanf("%d%d%d", &u, &v, &w);
            addEdge(u, v, w);
            addEdge(v, u, w);
        }
        for(int i = 0; i < q; i++){
            int u, v;
            scanf("%d%d", &u, &v);
            addQ(u, v, i);
            addQ(v, u, i);
        }

        tarjan(1, -1, q);

        for(int i = 0; i < q; i++){
            printf("%d\n", d[qe[2*i].v] + d[qe[2*i + 1].v] - 2*d[pa[i]]);
        }
    }
}

思路 —— RMQ做法

#include <iostream>
#include <cstdio>
#include <stack>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
const int N = 40000 + 5;
typedef long long ll;

struct edge{
    int v, w, nxt;
};
edge e[N << 1];
int head[N], tot;
int dp[N << 1][21], mp[N << 1], pos[N], d[N], dfn, totDp;

inline void init(){
    memset(head, -1, sizeof(head));
    d[1] = tot = dfn = totDp = 0;
}

inline void addEdge(int u, int v, int w){
    e[tot] = edge{v, w, head[u]};
    head[u] = tot++;
}

void dfs(int u, int pre){
    int curDfn = ++dfn;
    dp[++totDp][0] = curDfn;
    mp[curDfn] = u;
    pos[u] = totDp;
    for(int i = head[u]; ~i; i = e[i].nxt){
        int v = e[i].v;
        if(v == pre) {
            continue;
        }
        d[v] = d[u] + e[i].w;

        dfs(v, u);

        dp[++totDp][0] = curDfn;
    }
}

void rmqInit(){
    for(int j = 1; (1 << j) <= totDp; j++){
        for(int i = 1; i + (1 << j) - 1 <= totDp; i++){
            dp[i][j] = min(dp[i][j - 1], dp[i + (1 << (j - 1))][j - 1]);
        }
    }
}

int getLca(int u, int v){
    int l = pos[u], r = pos[v];
    if(l > r) {
        swap(l, r);
    }

    int j = (int)log2(r - l + 1);
    return mp[min(dp[l][j], dp[r - (1 << j) + 1][j])];
}

int main(){
    int t;
    scanf("%d", &t);
    while(t--){
        init();
        int n, m;
        scanf("%d%d", &n, &m);
        for(int i = 1; i <= n - 1; i++){
            int u, v, w;
            scanf("%d%d%d", &u, &v, &w);
            addEdge(u, v, w);
            addEdge(v, u, w);
        }
        dfs(1, -1);
        rmqInit();

        while(m--){
            int u, v;
            scanf("%d%d", &u, &v);
            printf("%d\n", d[u] + d[v] - 2*d[getLca(u, v)]);
        }
    }
}

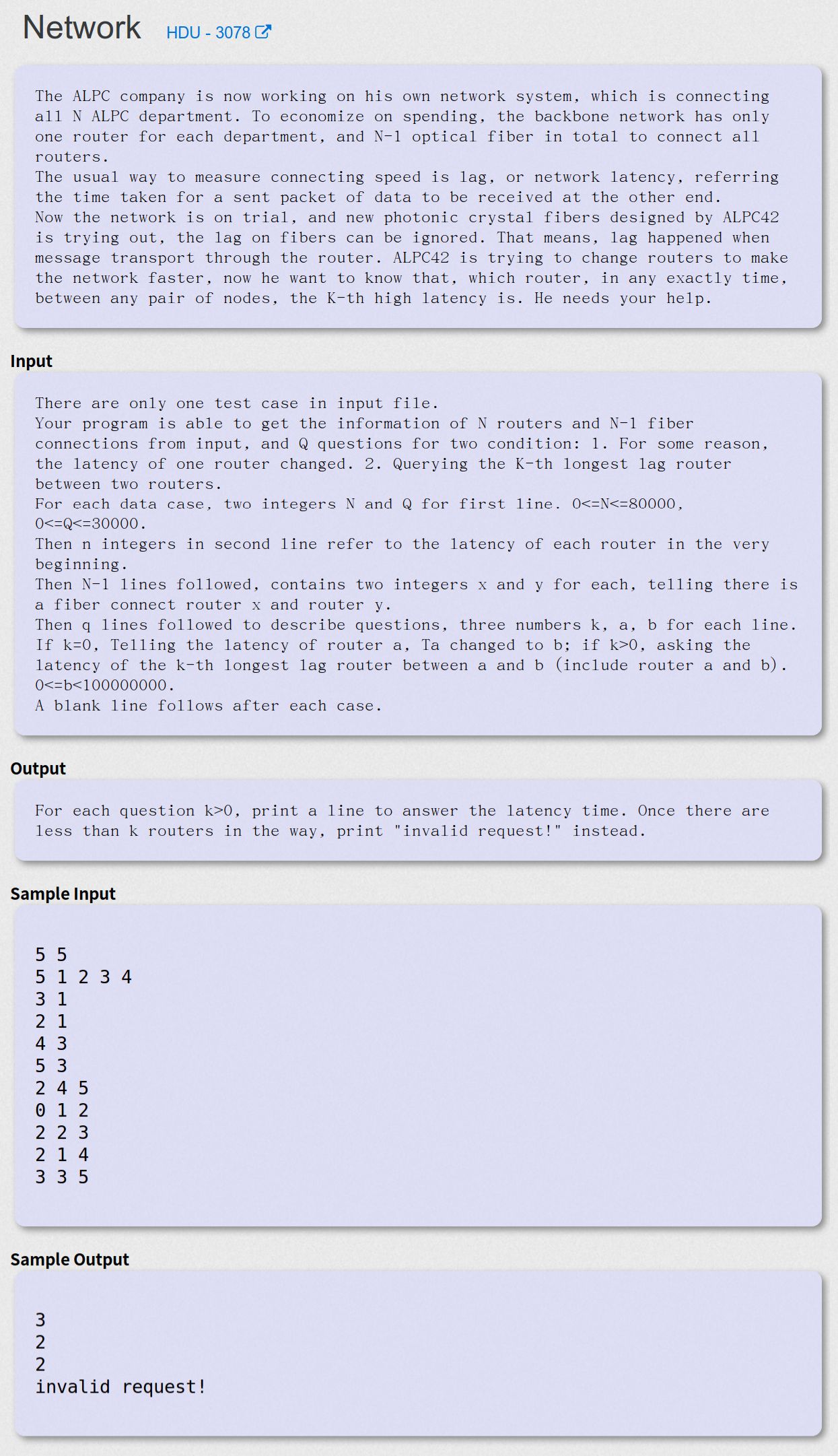
Network - HDU - 3078

题意
给定一棵数，求u到v的路径中第k大权值，或者修改点u的权值
思路 —— 暴力
没想打暴力可取 = =||
注意，这个第k大是真的第k大，不是第k小

#include <iostream>
#include <cstdio>
#include <vector>
#include <cstring>
#include <algorithm>
#include <functional>
using namespace std;
const int N = 80000 + 5;
const int BASE = 16;
typedef long long ll;

struct edge{
    int v, nxt;
};
edge e[N << 1];
int  head[N], tot;
int  fa[N][17], dpt[N], val[N];

inline void init(){
    memset(head, -1, sizeof(head));
    memset(fa, -1, sizeof(fa));
    dpt[1] = 0;
    tot = 0;
}

inline void addEdge(int u, int v){
    e[tot] = edge{v, head[u]};
    head[u] = tot++;
}

void dfs(int u, int pre){
    for(int i = head[u]; ~i; i = e[i].nxt){
        int v = e[i].v;
        if(v == pre)    continue;
        dpt[v] = dpt[u] + 1;
        fa[v][0] = u;
        dfs(v, u);
    }
}

void getFa(int n){
    for(int j = 1; j <= BASE; j++){
        for(int i = 1; i <= n; i++){
            if(fa[i][j - 1] == -1)  continue;
            fa[i][j] = fa[fa[i][j - 1]][j - 1];
        }
    }
}

int getLca(int u, int v){
    if(dpt[u] > dpt[v])     swap(u, v);
    for(int j = BASE; j >= 0; j--){
        if(fa[v][j] == -1 || dpt[fa[v][j]] < dpt[u])    continue;
        v = fa[v][j];
    }
    if(u == v)  return u;
    for(int j = BASE; j >= 0; j--){
        if(fa[u][j] == -1 || fa[v][j] == -1 || fa[u][j] == fa[v][j])    continue;
        u = fa[u][j], v = fa[v][j];
    }
    return fa[u][0];
}

int main(){
    int n, m;
    while(~scanf("%d%d", &n, &m)){
        init();
        for(int i = 1; i <= n; i++){
            scanf("%d", &val[i]);
        }
        for(int i = 1; i <= n - 1; i++){
            int u, v;
            scanf("%d%d", &u, &v);
            addEdge(u, v);
            addEdge(v, u);
        }
        dfs(1, -1);
        getFa(n);

        while(m--){
            int k, u, v;
            scanf("%d%d%d", &k, &u, &v);
            if(!k){
                val[u] = v;
            }else{
                k--;
                vector<int> vec;
                int ulca = getLca(u, v);
                for(int tmp = u; tmp != ulca; tmp = fa[tmp][0])     vec.push_back(val[tmp]);
                for(int tmp = v; tmp != ulca; tmp = fa[tmp][0])     vec.push_back(val[tmp]);
                vec.push_back(val[ulca]);
                sort(vec.begin(), vec.end(), greater<int>());
                if(k >= vec.size())     puts("invalid request!");
                else                    printf("%d\n", vec[k]);
            }
        }
    }
}

Bond - UVA - 11354

题意
给定一幅图，求u到v的边中的最大权值，要求该权值最小
思路 —— MST + LCA倍增
首先由于要求最大权值最小，所以跑最小生成树
然后用LCA倍增，维护dp[i][j]状态下的权值最下值
查询时再不断更新答案即可

  #include <iostream>
  #include <cstdio>
  #include <vector>
  #include <cstring>
  #include <algorithm>
  #include <functional>
  using namespace std;
  const int N = 5e4 + 5;
  const int M = 1e5 + 5;
  const int BASE = 16;
  typedef long long ll;

  struct kedge{
      int u, v, w;
      bool operator < (const kedge& b) const{ return w < b.w; }
  }in[M];

  struct edge{
      int v, w, nxt;
  };
  edge e[M << 1];
  int  head[N], tot;
  int  fa[N][17], dp[N][17], dpt[N], val[N];
  int  ft[N];

  inline void init(){
      for(int i = 0; i < N; i++)  ft[i] = i;
      memset(head, -1, sizeof(head));
      memset(fa, -1, sizeof(fa));
      dpt[1] = 0;
      tot = 0;
  }

  int find(int x){ return ft[x] == x ? x : ft[x] = find(ft[x]); }
  void merge(int x, int y){
      int p = find(x), q = find(y);
      if(p != q)   ft[q] = p;
  }

  inline void addEdge(int u, int v, int w){
      e[tot] = edge{v, w, head[u]};
      head[u] = tot++;
  }

  void Kruskal(int m){
      sort(in, in + m);
      for(int i = 0; i < m; i++){
          if(find(in[i].u) == find(in[i].v))  continue;
          merge(in[i].u, in[i].v);
          addEdge(in[i].u, in[i].v, in[i].w);
          addEdge(in[i].v, in[i].u, in[i].w);
      }
  }

  void dfs(int u, int pre){
      for(int i = head[u]; ~i; i = e[i].nxt){
          int v = e[i].v;
          if(v == pre)    continue;
          dpt[v] = dpt[u] + 1;
          fa[v][0] = u;
          dp[v][0] = e[i].w;
          dfs(v, u);
      }
  }

  void getFa(int n){
      for(int j = 1; j <= BASE; j++){
          for(int i = 1; i <= n; i++){
              if(fa[i][j - 1] == -1)  continue;
              fa[i][j] = fa[fa[i][j - 1]][j - 1];
              dp[i][j] = max(dp[i][j - 1], dp[fa[i][j - 1]][j - 1]);
          }
      }
  }

  int getLca(int u, int v){
      int ans = 0;
      if(dpt[u] > dpt[v])     swap(u, v);
      for(int j = BASE; j >= 0; j--){
          if(fa[v][j] == -1 || dpt[fa[v][j]] < dpt[u])    continue;
          ans = max(ans, dp[v][j]);
          v = fa[v][j];
      }
      if(u == v){
          //ans = max(ans, dp[v][0]);
          return ans;
      }
      for(int j = BASE; j >= 0; j--){
          if(fa[u][j] == -1 || fa[v][j] == -1 || fa[u][j] == fa[v][j])    continue;
          ans = max(ans, dp[v][j]);
          ans = max(ans, dp[u][j]);
          u = fa[u][j], v = fa[v][j];
      }
      ans = max(ans, dp[v][0]);
      ans = max(ans, dp[u][0]);
      //ans = max(ans, dp[fa[u][0]][0]);
      return ans;
  }

  int main(){
      bool first = true;
      int n, m;
      while(~scanf("%d%d", &n, &m)){
          if(!first)  puts("");
          else        first = false;

          init();
          for(int i = 0; i < m; i++){
              scanf("%d%d%d", &in[i].u, &in[i].v, &in[i].w);
          }
          Kruskal(m);

          dfs(1, -1);
          getFa(n);

          int q;
          scanf("%d", &q);
          while(q--){
              int u, v;
              scanf("%d%d", &u, &v);
              printf("%d\n", getLca(u, v));
          }
      }
  }

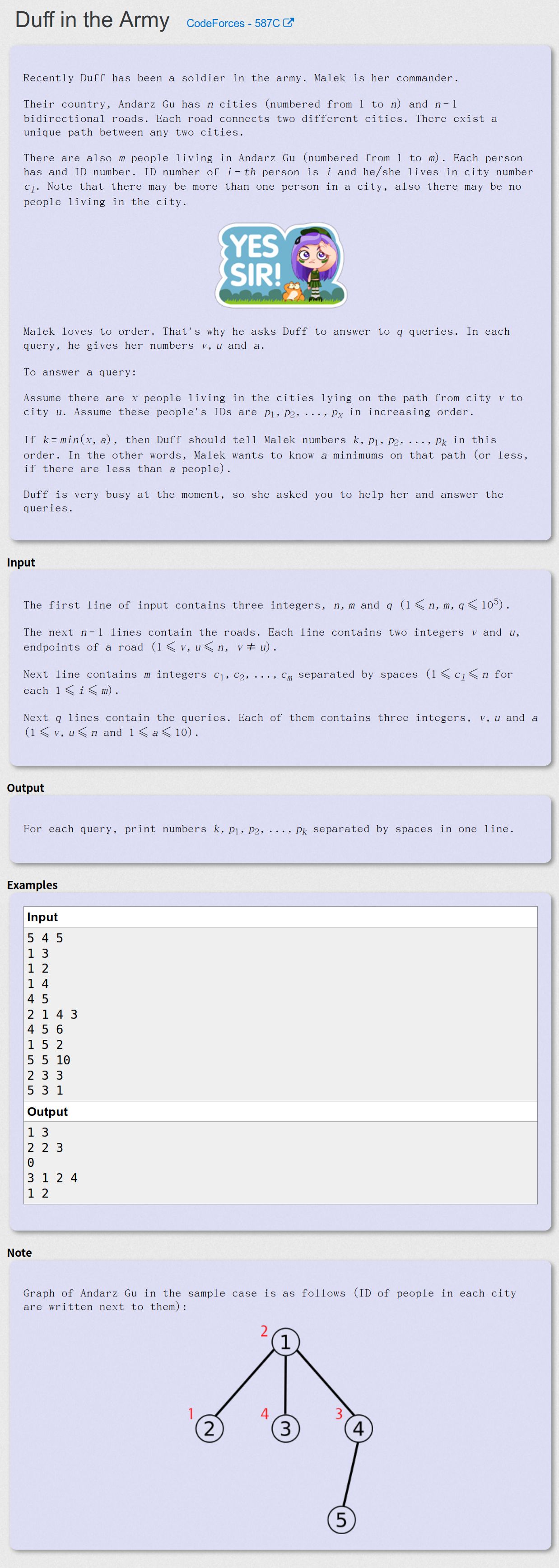
Duff in the Army - CodeForces - 587C

题意
给定一棵树，树上的点有一些权值（可能不止1个，也可能没有），现问从u到v路径中的前a小的数是什么（a <= 10)
思路 —— LCA倍增 + 归并排序思想
用LCA倍增维护每个点存在的值，因为是单调递增的，所以用LCA倍增维护时可以用归并排序合并维护，查询的时候也是合并更新即可

  #include <iostream>
  #include <cstdio>
  #include <vector>
  #include <cstring>
  #include <algorithm>
  #include <functional>
  using namespace std;
  const int N = 100000 + 5;
  const int BASE = 17;
  typedef long long ll;

  struct edge{
      int v, nxt;
  };
  edge e[N << 1];
  int  head[N], tot;
  int  fa[N][18], dpt[N];
  vector<int> vec[N][21];

  inline void init(){
      for(int i = 0; i < N; i++){
          for(int j = 0; j < 21; j++){
              vec[i][j].clear();
          }
      }
      memset(head, -1, sizeof(head));
      memset(fa, -1, sizeof(fa));
      dpt[1] = 0;
      tot = 0;
  }

  inline void addEdge(int u, int v){
      e[tot] = edge{v, head[u]};
      head[u] = tot++;
  }

  void dfs(int u, int pre){
      for(int i = head[u]; ~i; i = e[i].nxt){
          int v = e[i].v;
          if(v == pre)    continue;
          dpt[v] = dpt[u] + 1;
          fa[v][0] = u;
          dfs(v, u);
      }
  }

  void getFa(int n){
      for(int j = 1; j <= BASE; j++){
          for(int i = 1; i <= n; i++){
              if(fa[i][j - 1] == -1)  continue;
              fa[i][j] = fa[fa[i][j - 1]][j - 1];

              int p = 0, q = 0;
              vector<int>& res = vec[i][j];
              vector<int>& t1 = vec[i][j - 1];
              vector<int>& t2 = vec[fa[i][j - 1]][j - 1];
              while((p < t1.size() || q < t2.size()) && res.size() < 10){
                  if(p == t1.size())          res.push_back(t2[q++]);
                  else if(q == t2.size())     res.push_back(t1[p++]);
                  else if(t1[p] < t2[q])      res.push_back(t1[p++]);
                  else                        res.push_back(t2[q++]);
              }
          }
      }
  }

  void mergeVec(vector<int>& ret, vector<int>& src){
      int p = 0, q = 0;
      vector<int> res;
      vector<int>& t1 = ret;
      vector<int>& t2 = src;
      while((p < t1.size() || q < t2.size()) && res.size() < 10){
          if(p == t1.size())          res.push_back(t2[q++]);
          else if(q == t2.size())     res.push_back(t1[p++]);
          else if(t1[p] < t2[q])      res.push_back(t1[p++]);
          else                        res.push_back(t2[q++]);
      }

      ret.clear();
      for(int i = 0; i < res.size(); i++){
          ret.push_back(res[i]);
      }
  }

  vector<int> getLca(int u, int v){
      vector<int> ret;
      if(dpt[u] > dpt[v])     swap(u, v);
      for(int j = BASE; j >= 0; j--){
          if(fa[v][j] == -1 || dpt[fa[v][j]] < dpt[u])    continue;
          mergeVec(ret, vec[v][j]);
          v = fa[v][j];
      }
      if(u == v){
          mergeVec(ret, vec[u][0]);
          return ret;
      }
      for(int j = BASE; j >= 0; j--){
          if(fa[u][j] == -1 || fa[v][j] == -1 || fa[u][j] == fa[v][j])    continue;
          mergeVec(ret, vec[u][j]);
          mergeVec(ret, vec[v][j]);
          u = fa[u][j], v = fa[v][j];
      }
      mergeVec(ret, vec[u][0]);
      mergeVec(ret, vec[v][0]);
      mergeVec(ret, vec[fa[u][0]][0]);
      return ret;
  }

  int main(){
      int n, m, q;
      while(~scanf("%d%d%d", &n, &m, &q)){
          init();
          for(int i = 1; i <= n - 1; i++){
              int u, v;
              scanf("%d%d", &u, &v);
              addEdge(u, v);
              addEdge(v, u);
          }
          for(int i = 1; i <= m; i++){
              int u;
              scanf("%d", &u);
              vec[u][0].push_back(i);
          }
          dfs(1, -1);
          getFa(n);

          while(q--){
              int u, v, mind;
              scanf("%d%d%d", &u, &v, &mind);
              vector<int> ans = getLca(u, v);
              printf("%d", min((int)ans.size(), mind));
              for(int i = 0; i < min((int)ans.size(), mind); i++){
                  printf(" %d", ans[i]);
              }
              puts("");
          }
      }
  }