树链剖分
前言
树链剖分入门!接下来可以切LCT了!
树链剖分说白了就是把树上信息抓到数据结构上,如线段树、Splay等,进行维护
漆子超在IOI2009国家集训队论文里写到了路径剖分与树分治的联系,一下子让本蒟蒻对树链剖分有了进一步的理解,建议各位dalao可以看看
http://blog.sina.com.cn/s/blog_6974c8b20100zc61.html
https://wenku.baidu.com/view/1bc2e4ea172ded630b1cb602.html
https://riteme.github.io/blog/2016-4-20/tree-split.html
Query on a tree - SPOJ QTREE

链接
https://cn.vjudge.net/problem/SPOJ-QTREE
题意
给定一棵树,有两种操作,第一种是改变第i条边的权值为ti,第二种是找出(u,v)路径上的边权最大值
思路
经典模板题,QTREE
#include <cstdio>
#include <algorithm>
#include <iostream>
#include <cstring>
#define lson l, m, rt << 1
#define rson m + 1, r, rt << 1 | 1
using namespace std;
const int N = 10000 + 5;
struct edge{
int v, w, nxt;
};
edge e[N << 1];
int head[N], tot;
int fa[N], top[N], son[N], sz[N], dpt[N];
int preew[N], mp[N], mptot;
int seg[N << 2];
int input[N][3];
inline void init(){
memset(head, -1, sizeof(head));
memset(seg, 0, sizeof(seg));
fa[1] = -1, dpt[1] = 0, preew[1] = -1;
tot = 0, mptot = 0;
}
inline void addEdge(int u, int v, int w){
e[tot] = edge{v, w, head[u]};
head[u] = tot++;
}
inline void pushUp(int rt){
seg[rt] = max(seg[rt << 1], seg[rt << 1 | 1]);
}
void update(int pos, int val, int l, int r, int rt){
if(l == r){
seg[rt] = val;
return;
}
int m = (l + r) >> 1;
if(pos <= m) update(pos, val, lson);
else update(pos, val, rson);
pushUp(rt);
}
int query(int ql, int qr, int l, int r, int rt){
if(ql <= l && r <= qr){
return seg[rt];
}
int ans = 0, m = (l + r) >> 1;
if(ql <= m) ans = max(ans, query(ql, qr, lson));
if(m < qr) ans = max(ans, query(ql, qr, rson));
return ans;
}
void dfs(int u){
son[u] = -1, sz[u] = 1;
for(int i = head[u]; ~i; i = e[i].nxt){
int v = e[i].v;
if(v == fa[u]) continue;
fa[v] = u;
preew[v] = e[i].w;
dpt[v] = dpt[u] + 1;
dfs(v);
sz[u] += sz[v];
if(son[u] == -1 || sz[son[u]] < sz[v]) son[u] = v;
}
}
void buildTree(int u, int rt, int n){
mp[u] = ++mptot, top[u] = rt;
update(mp[u], preew[u], 1, n, 1);
if(~son[u]) buildTree(son[u], rt, n);
for(int i = head[u]; ~i; i = e[i].nxt){
int v = e[i].v;
if(v == fa[u] || v == son[u]) continue;
buildTree(v, v, n);
}
}
void solveUpdate(int idx, int val){
int v = dpt[input[idx][0]] > dpt[input[idx][1]] ? input[idx][0] : input[idx][1];
update(mp[v], val, 1, mptot, 1);
}
int solveQuery(int u, int v, int n){
int fu = top[u], fv = top[v], ret = 0;
while(fu != fv){
if(dpt[fu] < dpt[fv]){
swap(fu, fv);
swap(u, v);
}
ret = max(ret, query(mp[fu], mp[u], 1, n, 1));
u = fa[fu], fu = top[u];
}
if(u == v) return ret;
if(dpt[u] > dpt[v]) swap(u, v);
// 最后是mp[u] + 1而不是mp[u]是因为维护的是父边,故mp[u]不在(u,v)路径上
return max(ret, query(mp[u] + 1, mp[v], 1, n, 1));
}
int main(){
int t;
scanf("%d", &t);
while(t--){
init();
int n;
scanf("%d", &n);
for(int i = 1; i <= n - 1; i++){
scanf("%d%d%d", &input[i][0], &input[i][1], &input[i][2]);
addEdge(input[i][0], input[i][1], input[i][2]);
addEdge(input[i][1], input[i][0], input[i][2]);
}
dfs(1);
buildTree(1, 1, n);
char op[7] = {0};
while(scanf("%s", op) && op[0] != 'D'){
int a, b;
scanf("%d%d", &a, &b);
if(op[0] == 'Q') printf("%d\n", solveQuery(a, b, n));
else solveUpdate(a, b);
}
}
}
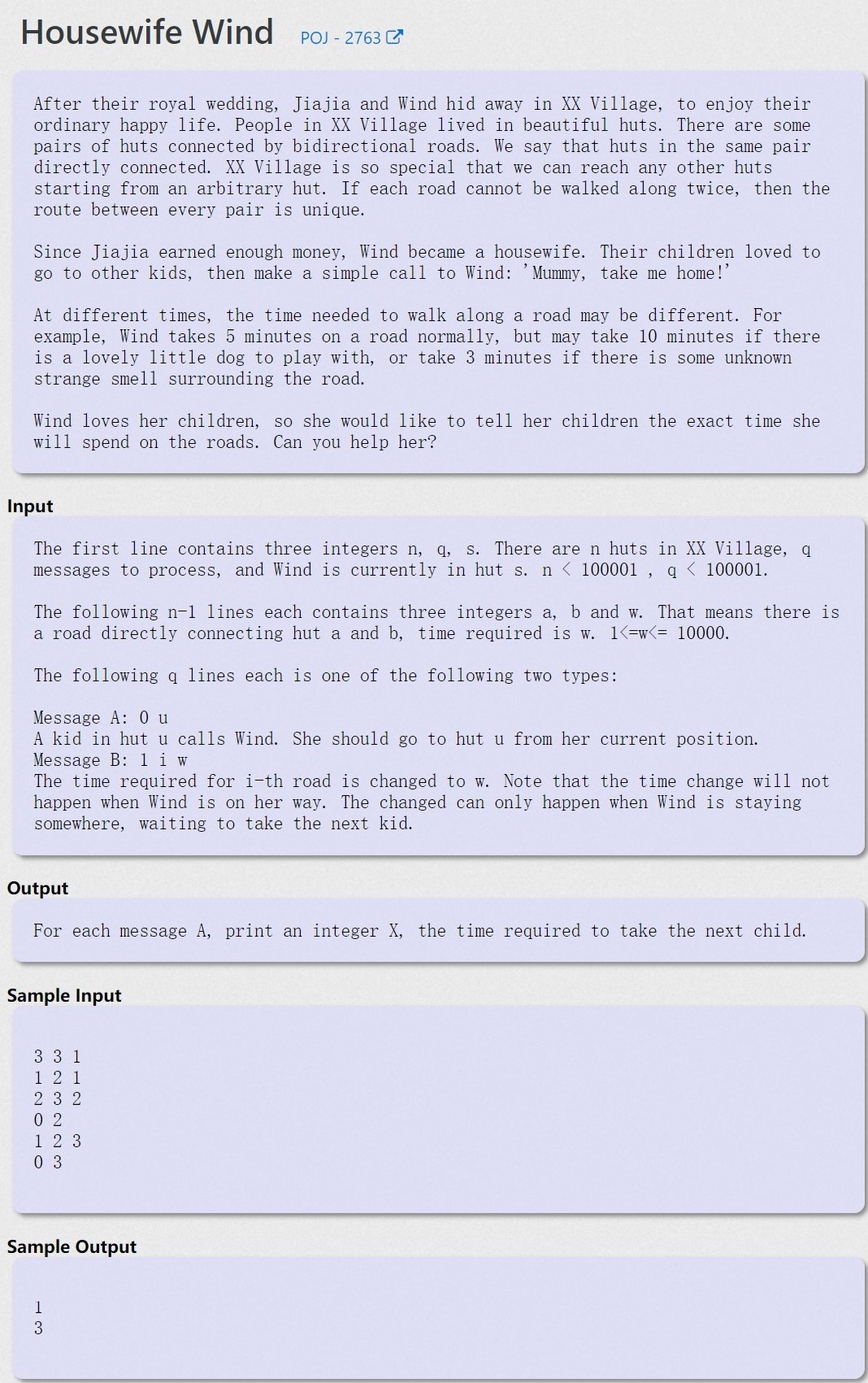
Housewife Wind - POJ 2763
链接
https://cn.vjudge.net/problem/POJ-2763
题意
给定一棵树,有两种操作,第一种从src点到des点,求出边权和,并把src变为des,第二种是修改第i条边的权值
思路
还是模板题系列
#include <cstdio>
#include <algorithm>
#include <iostream>
#include <cstring>
#define lson l, m, rt << 1
#define rson m + 1, r, rt << 1 | 1
using namespace std;
const int N = 100001 + 5;
struct edge{
int v, w, nxt;
};
edge e[N << 1];
int head[N], tot;
int fa[N], top[N], son[N], sz[N], dpt[N];
int preew[N], mp[N], mptot;
int seg[N << 2];
int input[N][3];
inline int read(){
char ch = getchar(); int x = 0, f = 1;
while(ch < '0' || ch > '9') {if(ch == '-') f = -1; ch = getchar();}
while('0' <= ch && ch <= '9') {x = x * 10 + ch - '0'; ch = getchar();}
return x * f;
}
inline void init(){
memset(head, -1, sizeof(head));
memset(seg, 0, sizeof(seg));
fa[1] = -1, dpt[1] = 0, preew[1] = -1;
tot = 0, mptot = 0;
}
inline void addEdge(int u, int v, int w){
e[tot] = edge{v, w, head[u]};
head[u] = tot++;
}
inline void pushUp(int rt){
seg[rt] = seg[rt << 1] + seg[rt << 1 | 1];
}
void update(int pos, int val, int l, int r, int rt){
if(l == r){
seg[rt] = val;
return;
}
int m = (l + r) >> 1;
if(pos <= m) update(pos, val, lson);
else update(pos, val, rson);
pushUp(rt);
}
int query(int ql, int qr, int l, int r, int rt){
if(ql <= l && r <= qr){
return seg[rt];
}
int ans = 0, m = (l + r) >> 1;
if(ql <= m) ans += query(ql, qr, lson);
if(m < qr) ans += query(ql, qr, rson);
return ans;
}
void dfs(int u){
son[u] = -1, sz[u] = 1;
for(int i = head[u]; ~i; i = e[i].nxt){
int v = e[i].v;
if(v == fa[u]) continue;
fa[v] = u;
preew[v] = e[i].w;
dpt[v] = dpt[u] + 1;
dfs(v);
sz[u] += sz[v];
if(son[u] == -1 || sz[son[u]] < sz[v]) son[u] = v;
}
}
void buildTree(int u, int rt, int n){
mp[u] = ++mptot, top[u] = rt;
update(mp[u], preew[u], 1, n, 1);
if(~son[u]) buildTree(son[u], rt, n);
for(int i = head[u]; ~i; i = e[i].nxt){
int v = e[i].v;
if(v == fa[u] || v == son[u]) continue;
buildTree(v, v, n);
}
}
void solveUpdate(int idx, int val){
int v = dpt[input[idx][0]] > dpt[input[idx][1]] ? input[idx][0] : input[idx][1];
update(mp[v], val, 1, mptot, 1);
}
int solveQuery(int u, int v, int n){
int fu = top[u], fv = top[v], ret = 0;
while(fu != fv){
if(dpt[fu] < dpt[fv]){
swap(fu, fv);
swap(u, v);
}
ret += query(mp[fu], mp[u], 1, n, 1);
u = fa[fu], fu = top[u];
}
if(u == v) return ret;
if(dpt[u] > dpt[v]) swap(u, v);
return ret + query(mp[u] + 1, mp[v], 1, n, 1);
}
int main(){
int n, q, src;
while(~scanf("%d%d%d", &n, &q, &src)){
init();
for(int i = 1; i <= n - 1; i++){
input[i][0] = read(), input[i][1] = read(), input[i][2] = read();
addEdge(input[i][0], input[i][1], input[i][2]);
addEdge(input[i][1], input[i][0], input[i][2]);
}
dfs(1);
buildTree(1, 1, n);
while(q--){
int op = read();
if(op == 0){
int des = read();
printf("%d\n", solveQuery(src, des, n));
src = des;
}else{
int idx = read(), val = read();
solveUpdate(idx, val);
}
}
}
}
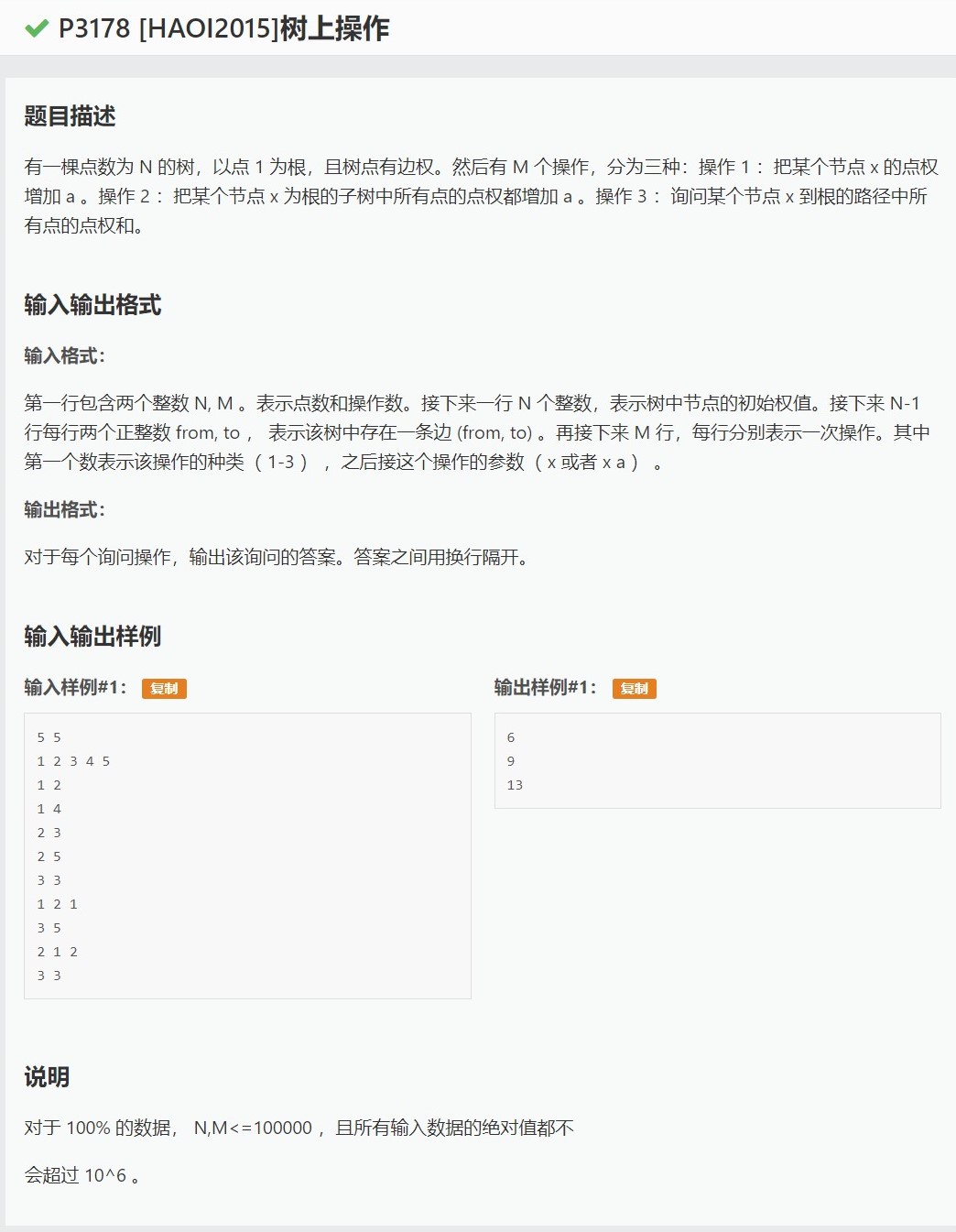
[HAOI2015]树上操作 - 洛谷P3178
链接
https://www.luogu.org/problemnew/show/P3178
思路
树链剖分用线段树维护点
这里有点儿小卡的地方是要修改子树信息而不是链信息,实际上根据DFS性质,点u的子树在线段树中不就是mp[u] + sz[u] - 1嘛,剩下同理
#include <cstdio>
#include <algorithm>
#include <iostream>
#include <cstring>
#define lson l, m, rt << 1
#define rson m + 1, r, rt << 1 | 1
using namespace std;
typedef long long ll;
const int N = 1e5 + 5;
struct edge{
int v, nxt;
};
struct Node{
int sum, l, r;
};
edge e[N << 1];
int head[N], tot;
int fa[N], top[N], son[N], sz[N], dpt[N];
int arr[N], mp[N], mptot;
ll lzy[N << 2], seg[N << 2];
inline int read(){
char ch = getchar(); int x = 0, f = 1;
while(ch < '0' || ch > '9') {if(ch == '-') f = -1; ch = getchar();}
while('0' <= ch && ch <= '9') {x = x * 10 + ch - '0'; ch = getchar();}
return x * f;
}
inline void init(){
memset(lzy, 0, sizeof(lzy));
memset(head, -1, sizeof(head));
fa[1] = -1, dpt[1] = 0;
tot = 0, mptot = 0;
}
inline void addEdge(int u, int v){
e[tot] = edge{v, head[u]};
head[u] = tot++;
}
inline void pushUp(int rt){
seg[rt] = seg[rt << 1] + seg[rt << 1 | 1];
}
inline void pushDown(int rt, int l, int r){
if(lzy[rt]){
int m = (l + r) >> 1;
seg[rt << 1] += lzy[rt] * (m - l + 1);
seg[rt << 1 | 1] += lzy[rt] * (r - m);
lzy[rt << 1] += lzy[rt];
lzy[rt << 1 | 1] += lzy[rt];
lzy[rt] = 0;
}
}
void update(int val, int ql, int qr, int l, int r, int rt){
if(ql <= l && r <= qr){
seg[rt] += (ll)val * (r - l + 1);
lzy[rt] += val;
return;
}
int m = (l + r) >> 1;
pushDown(rt, l, r);
if(ql <= m) update(val, ql, qr, lson);
if(m < qr) update(val, ql, qr, rson);
pushUp(rt);
}
ll query(int ql, int qr, int l, int r, int rt){
if(ql <= l && r <= qr){
return seg[rt];
}
pushDown(rt, l, r);
int m = (l + r) >> 1;
ll ans = 0;
if(ql <= m) ans += query(ql, qr, lson);
if(m < qr) ans += query(ql, qr, rson);
return ans;
}
void dfs(int u){
son[u] = -1, sz[u] = 1;
for(int i = head[u]; ~i; i = e[i].nxt){
int v = e[i].v;
if(v == fa[u]) continue;
fa[v] = u;
dpt[v] = dpt[u] + 1;
dfs(v);
sz[u] += sz[v];
if(son[u] == -1 || sz[son[u]] < sz[v]) son[u] = v;
}
}
void buildTree(int u, int rt, int n){
mp[u] = ++mptot, top[u] = rt;
update(arr[u], mptot, mptot, 1, n, 1);
if(~son[u]) buildTree(son[u], rt, n);
for(int i = head[u]; ~i; i = e[i].nxt){
int v = e[i].v;
if(v == fa[u] || v == son[u]) continue;
buildTree(v, v, n);
}
}
inline ll solveQuery(int u, int n){
int fu = top[u];
ll ans = 0;
while(fu != 1){
ans += query(mp[fu], mp[u], 1, n, 1);
u = fa[fu], fu = top[u];
}
ans += query(mp[1], mp[u], 1, n, 1);
return ans;
}
inline void solveUpdateSingle(int u, int val, int n){
update(val, mp[u], mp[u], 1, n, 1);
}
inline void solveUpdateRange(int u, int val, int n){
update(val, mp[u], mp[u] + sz[u] - 1, 1, n ,1);
}
int main(){
init();
int n = read(), m = read();
for(int i = 1; i <= n; i++){
arr[i] = read();
}
for(int i = 1; i <= n - 1; i++){
int u = read(), v = read();
addEdge(u, v);
addEdge(v, u);
}
dfs(1);
buildTree(1, 1, n);
while(m--){
int op = read();
if(op == 1){
int u = read(), val = read();
solveUpdateSingle(u, val, n);
}else if(op == 2){
int u = read(), val = read();
solveUpdateRange(u, val, n);
}else{
int u = read();
printf("%lld\n", solveQuery(u, n));
}
}
}
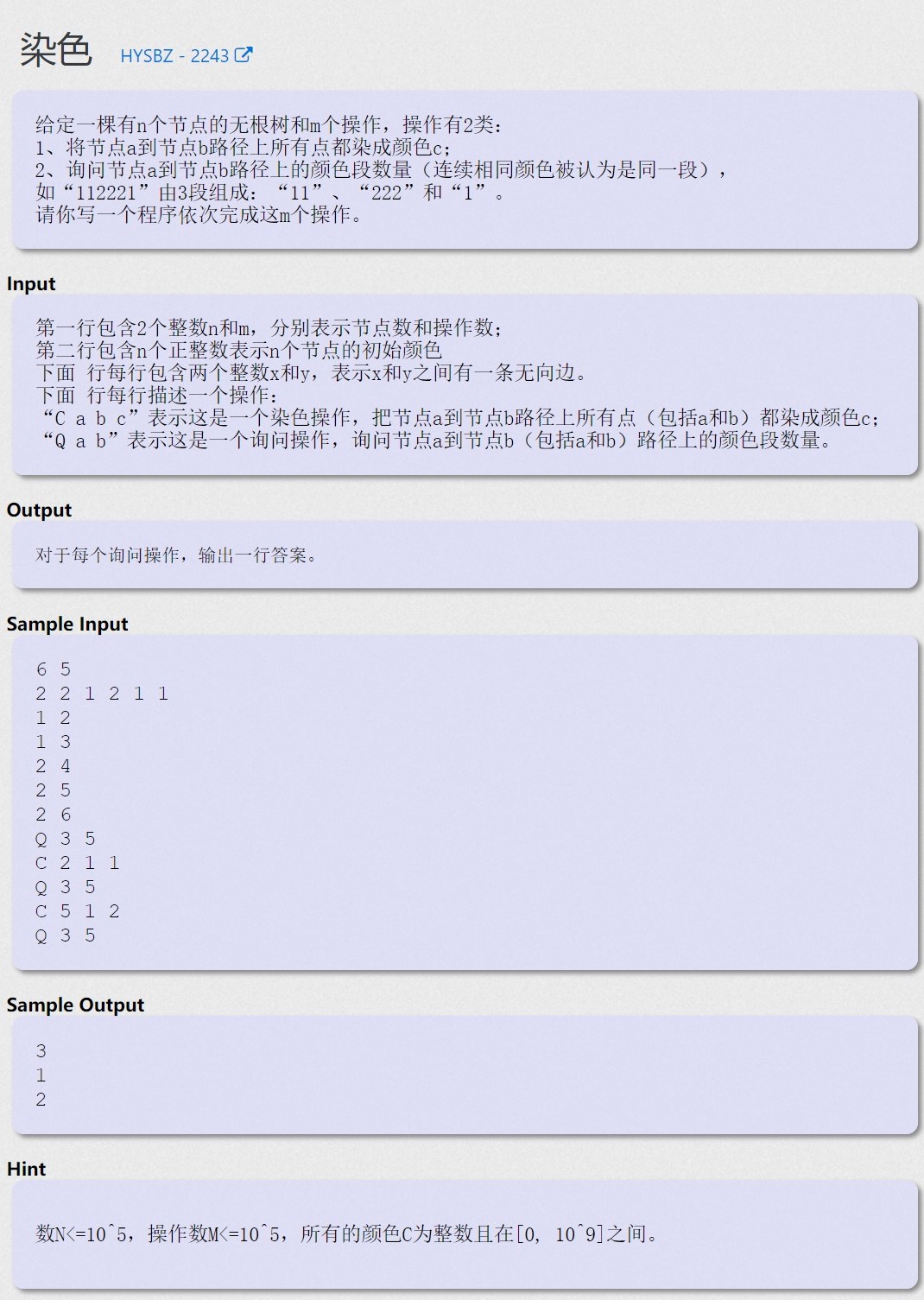
染色 - HYSBZ 2243
链接
https://cn.vjudge.net/problem/HYSBZ-2243
思路
模板题的味道稍稍轻了点
首先是考虑维护颜色段信息,那当然是线段树直接维护左右端点和当前的颜色段数量,合并的时候查左区间右端点和右区间左端点,一样就答案和减1,不一样就答案和
然后是查询(u,v)的颜色段信息,记lca(u, v) = rt,则窝们要搞到的就是(rt, u]与[rt, v](rt点只能有一端是闭区间),所以就朝这个目标不断合并即可,注意合并的位置问题(即该合并在左边还是右边),最后得到后查rt端的左右端点是否相同,若相同答案和减1,若不同则是答案和
#include <cstdio>
#include <algorithm>
#include <iostream>
#include <cstring>
#define lson l, m, rt << 1
#define rson m + 1, r, rt << 1 | 1
using namespace std;
const int N = 1e5 + 5;
struct edge{
int v, nxt;
};
struct Node{
int sum, l, r;
};
edge e[N << 1];
int head[N], tot;
int fa[N], top[N], son[N], sz[N], dpt[N];
int arr[N], color[N], mp[N], mptot;
int lzy[N << 2];
Node seg[N << 2];
inline int read(){
char ch = getchar(); int x = 0, f = 1;
while(ch < '0' || ch > '9') {if(ch == '-') f = -1; ch = getchar();}
while('0' <= ch && ch <= '9') {x = x * 10 + ch - '0'; ch = getchar();}
return x * f;
}
inline void init(){
memset(lzy, -1, sizeof(lzy));
memset(head, -1, sizeof(head));
fa[1] = -1, dpt[1] = 0;
tot = 0, mptot = 0;
}
inline void addEdge(int u, int v){
e[tot] = edge{v, head[u]};
head[u] = tot++;
}
Node merge(const Node& a, const Node& b){
if(a.l == -1 && a.r == -1){
return b;
}else if(b.l == -1 && b.r == -1){
return a;
}
Node ret{a.sum + b.sum, a.l, b.r};
if(a.r == b.l) ret.sum--;
return ret;
}
inline void pushUp(int rt){
seg[rt] = merge(seg[rt << 1], seg[rt << 1 | 1]);
}
inline void pushDown(int rt){
if(~lzy[rt]){
seg[rt << 1] = seg[rt << 1 | 1] = Node{1, lzy[rt], lzy[rt]};
lzy[rt << 1] = lzy[rt << 1 | 1] = lzy[rt];
lzy[rt] = -1;
}
}
void build(int l, int r, int rt){
if(l == r){
seg[rt] = {1, arr[l], arr[l]};
return;
}
int m = (l + r) >> 1;
build(lson);
build(rson);
pushUp(rt);
}
void update(int val, int ql, int qr, int l, int r, int rt){
if(ql <= l && r <= qr){
seg[rt] = Node{1, val, val};
lzy[rt] = val;
return;
}
int m = (l + r) >> 1;
pushDown(rt);
if(ql <= m) update(val, ql, qr, lson);
if(m < qr) update(val, ql, qr, rson);
pushUp(rt);
}
void query(Node& ans, int ql, int qr, int l, int r, int rt){
if(ql <= l && r <= qr){
ans = merge(ans, seg[rt]);
return;
}
pushDown(rt);
int m = (l + r) >> 1;
if(ql <= m) query(ans, ql, qr, lson);
if(m < qr) query(ans, ql, qr, rson);
}
void dfs(int u){
son[u] = -1, sz[u] = 1;
for(int i = head[u]; ~i; i = e[i].nxt){
int v = e[i].v;
if(v == fa[u]) continue;
fa[v] = u;
dpt[v] = dpt[u] + 1;
dfs(v);
sz[u] += sz[v];
if(son[u] == -1 || sz[son[u]] < sz[v]) son[u] = v;
}
}
void buildTree(int u, int rt, int n){
mp[u] = ++mptot, top[u] = rt;
arr[mptot] = color[u];
if(~son[u]) buildTree(son[u], rt, n);
for(int i = head[u]; ~i; i = e[i].nxt){
int v = e[i].v;
if(v == fa[u] || v == son[u]) continue;
buildTree(v, v, n);
}
}
int solveQuery(int u, int v, int n){
int fu = top[u], fv = top[v];
Node tu = Node{0, -1, -1}, tv = Node{0, -1, -1}, tmp;
while(fu != fv){
tmp = Node{0, -1, -1};
if(dpt[fu] < dpt[fv]){
swap(fu, fv);
swap(u, v);
swap(tu, tv);
}
query(tmp, mp[fu], mp[u], 1, n, 1);
tu = merge(tmp, tu);
u = fa[fu], fu = top[u];
}
tmp = Node{0, -1, -1};
if(dpt[u] < dpt[v]){
swap(fu, fv);
swap(u, v);
swap(tu, tv);
}
query(tmp, mp[v], mp[u], 1, n, 1);
tu = merge(tmp, tu);
int ans = tu.sum + tv.sum;
if(tu.l == tv.l) ans--;
return ans;
}
void solveUpdate(int u, int v, int val, int n){
int fu = top[u], fv = top[v];
while(fu != fv){
if(dpt[fu] < dpt[fv]){
swap(fu, fv);
swap(u, v);
}
update(val, mp[fu], mp[u], 1, n, 1);
u = fa[fu], fu = top[u];
}
if(dpt[u] > dpt[v]) swap(u, v);
update(val, mp[u], mp[v], 1, n, 1);
}
int main(){
init();
int n = read(), m = read();
for(int i = 1; i <= n; i++){
color[i] = read();
}
for(int i = 1; i <= n - 1; i++){
int u = read(), v = read();
addEdge(u, v);
addEdge(v, u);
}
dfs(1);
buildTree(1, 1, n);
build(1, n, 1);
while(m--){
char op[2];
scanf("%s", op);
if(op[0] == 'Q'){
int u = read(), v = read();
printf("%d\n", solveQuery(u, v, n));
}else{
int u = read(), v = read(), val = read();
solveUpdate(u, v, val, n);
}
}
}


