刷题记（LCT - I） —— 2018.11.23

LCT门槛？

前言

不算LCT入门，但至少大概大概懂了LCT的基本原理
个人感觉LCT系列不写个三四篇是没办法大概深入理解的 QAQ

QTREE解法的一些研究
https://wenku.baidu.com/view/75906f160b4e767f5acfcedb.html
LCT讲解
http://www.cnblogs.com/flashhu/p/8324551.html

洛谷P3690 -【模板】Link Cut Tree （动态树）

链接
https://www.luogu.org/problemnew/show/P3690
思路
LCT模板题，拿来试模板

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#define lson ch[x][0]
#define rson ch[x][1]
using namespace std;
typedef long long ll;
const int N = 3e5 + 15;
const int inf = 0x3f3f3f3f;

inline int read(){
    int x = 0;
    char ch;
    while((ch = getchar()) < '0' || ch > '9');
    while('0' <= ch && ch <= '9'){
        x = x * 10 + ch - '0';
        ch = getchar();
    }
    return x;
}

struct LinkCutTree{
    int fa[N], ch[N][2], sum[N], val[N], lzy[N];
    int stk[N];

    inline bool nRoot(int x){
        return ch[fa[x]][0] == x || ch[fa[x]][1] == x;
    }

    void pushUp(int x){
        sum[x] = sum[lson] ^ sum[rson] ^ val[x];
    }

    void pushR(int x){
        swap(lson, rson);
        lzy[x] ^= 1;
    }

    void pushDown(int x){
        if(lzy[x]){
            if(lson)    pushR(lson);
            if(rson)    pushR(rson);
            lzy[x] = 0;
        }
    }

    void rotate(int x){
        int y = fa[x], z = fa[y];
        int p = (ch[y][1] == x), w = ch[x][p^1];
        if(nRoot(y))    ch[z][ch[z][1] == y] = x;
        ch[x][p^1] = y, ch[y][p] = w;
        if(w)   fa[w] = y;
        fa[y] = x, fa[x] = z;
        pushUp(y);
    }

    void splay(int x){
        int pstk = 0, y = x;
        for(y = x; nRoot(y); y = fa[y]){
            stk[++pstk] = y;
        }
        stk[++pstk] = y;
        while(pstk)     pushDown(stk[pstk--]);

        while(nRoot(x)){
            int y = fa[x], z = fa[y];
            if(nRoot(y))     rotate((ch[y][0] == x) ^ (ch[z][0] == y) ? x : y);
            rotate(x);
        }
        pushUp(x);
    }

    void access(int x){
        for(int y = 0; x; y = x, x = fa[x]){
            splay(x);
            rson = y;
            pushUp(x);
        }
    }

    void makeRoot(int x){
        access(x);
        splay(x);
        pushR(x);
    }

    int findRoot(int x){
        access(x);
        splay(x);
        while(lson){
            pushDown(x);
            x = lson;
        }
        return x;
    }

    void split(int x, int y){
        makeRoot(x);
        access(y);
        splay(y);
    }

    void link(int x, int y){
        makeRoot(x);
        if(findRoot(y) != x)    fa[x] = y;
    }

    void cut(int x, int y){
        makeRoot(x);
        if(findRoot(y) == x && fa[x] == y && !rson){
            fa[x] = ch[y][0] = 0;
            pushUp(y);
        }
    }
};

LinkCutTree lct;

int main(){
    int n = read(), m = read();
    for(int i = 1; i <= n; i++){
        lct.val[i] = read();
    }
    while(m--){
        int op = read(), x = read(), y = read();
        switch(op){
        case 0:
            lct.split(x, y);
            printf("%d\n", lct.sum[y]);
            break;
        case 1:
            lct.link(x, y);
            break;
        case 2:
            lct.cut(x, y);
            break;
        case 3:
            lct.splay(x);
            lct.val[x] = y;
            break;
        }
    }
}

Query on a tree - SPOJ QTREE

链接
https://cn.vjudge.net/problem/SPOJ-QTREE
题意
给定一棵树，有两种操作，第一种是改变第i条边的权值为ti，第二种是找出(u,v)路径上的边权最大值
思路
LCT模板题
不过现在是维护边值，可以把(u, v)的边当作点插入，即(u, e)和(e, v)即可

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#define lson ch[x][0]
#define rson ch[x][1]
using namespace std;
typedef long long ll;
const int N = 2e4 + 15;
const int inf = 0x3f3f3f3f;

inline int read(){
    int x = 0;
    char ch;
    while((ch = getchar()) < '0' || ch > '9');
    while('0' <= ch && ch <= '9'){
        x = x * 10 + ch - '0';
        ch = getchar();
    }
    return x;
}

struct LinkCutTree{
    int fa[N], ch[N][2], sum[N], val[N], lzy[N];
    int stk[N];

    void init(){
        #define met(x) memset(x, 0, sizeof(x))
        met(fa);
        met(ch);
        met(sum);
        met(lzy);
        met(val);
    }

    inline bool nRoot(int x){
        return ch[fa[x]][0] == x || ch[fa[x]][1] == x;
    }

    void pushUp(int x){
        sum[x] = max(val[x], max(sum[lson], sum[rson]));
    }

    void pushR(int x){
        swap(lson, rson);
        lzy[x] ^= 1;
    }

    void pushDown(int x){
        if(lzy[x]){
            if(lson)    pushR(lson);
            if(rson)    pushR(rson);
            lzy[x] = 0;
        }
    }

    void rotate(int x){
        int y = fa[x], z = fa[y];
        int p = (ch[y][1] == x), w = ch[x][p^1];
        if(nRoot(y))    ch[z][ch[z][1] == y] = x;
        ch[x][p^1] = y, ch[y][p] = w;
        if(w)   fa[w] = y;
        fa[y] = x, fa[x] = z;
        pushUp(y);
    }

    void splay(int x){
        int pstk = 0, y = x;
        for(y = x; nRoot(y); y = fa[y]){
            stk[++pstk] = y;
        }
        stk[++pstk] = y;
        while(pstk)     pushDown(stk[pstk--]);

        while(nRoot(x)){
            int y = fa[x], z = fa[y];
            if(nRoot(y))     rotate((ch[y][0] == x) ^ (ch[z][0] == y) ? x : y);
            rotate(x);
        }
        pushUp(x);
    }

    void access(int x){
        for(int y = 0; x; y = x, x = fa[x]){
            splay(x);
            rson = y;
            pushUp(x);
        }
    }

    void makeRoot(int x){
        access(x);
        splay(x);
        pushR(x);
    }

    int findRoot(int x){
        access(x);
        splay(x);
        while(lson){
            pushDown(x);
            x = lson;
        }
        return x;
    }

    void split(int x, int y){
        makeRoot(x);
        access(y);
        splay(y);
    }

    void link(int x, int y){
        makeRoot(x);
        if(findRoot(y) != x)    fa[x] = y;
    }

    void cut(int x, int y){
        makeRoot(x);
        if(findRoot(y) == x && fa[x] == y && !rson){
            fa[x] = ch[y][0] = 0;
            pushUp(y);
        }
    }
};

LinkCutTree lct;
char op[10];

int main(){
    int t = read();
    while(t--){
        lct.init();
        int n = read();
        for(int i = 1; i <= n - 1; i++){
            int u = read(), v = read(), w = read();
            lct.link(i + n, v);
            lct.link(u, i + n);
            lct.splay(i + n);
            lct.val[i + n] = w;
        }

        while(scanf("%s", op) && op[0] != 'D'){
            int x = read(), y = read();
            if(op[0] == 'Q'){
                lct.split(x, y);
                printf("%d\n", lct.sum[y]);
            }else{
                lct.splay(x + n);
                lct.val[x + n] = y;
            }
        }
    }
}

Bounce 弹飞绵羊 - HYSBZ 2002

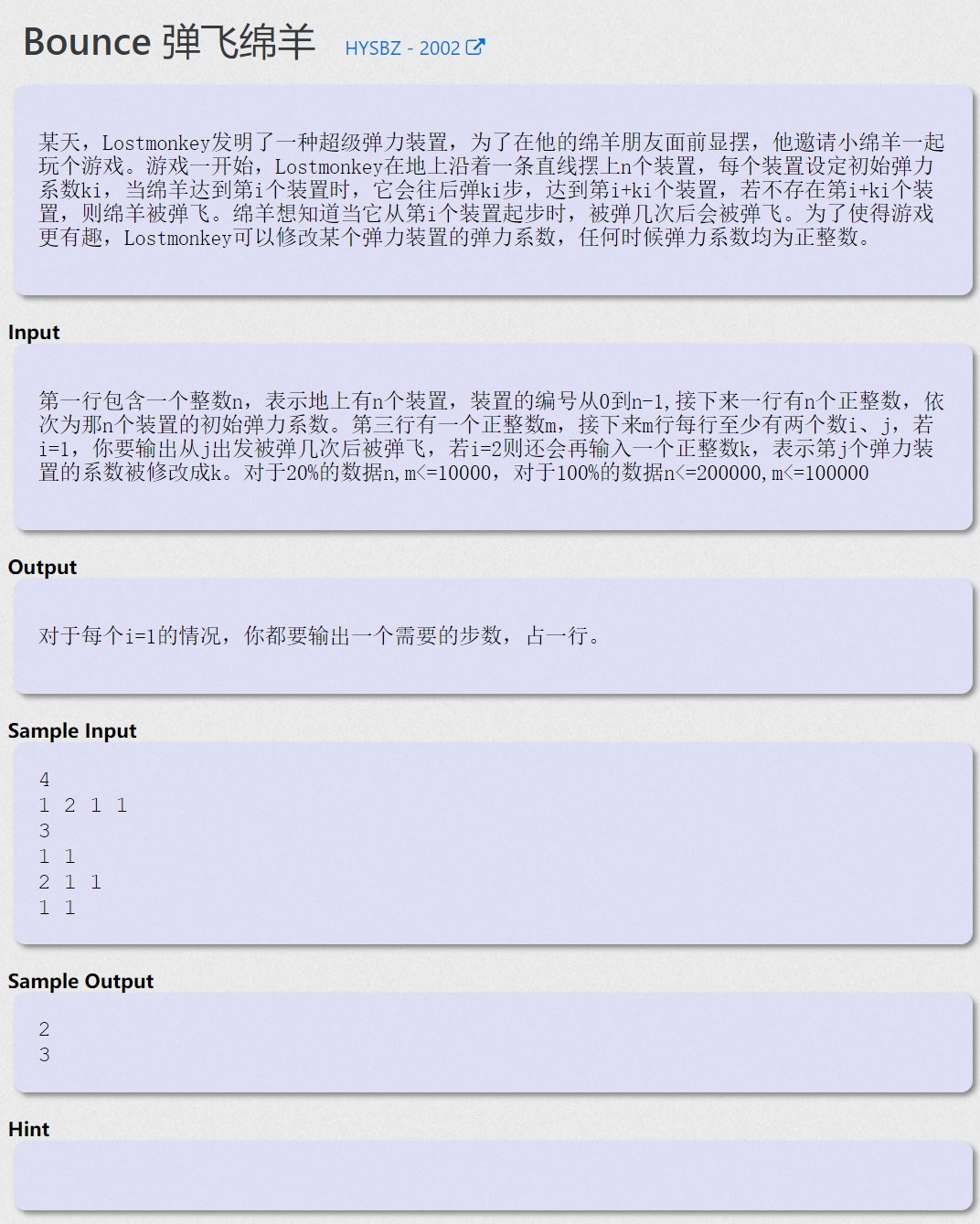
链接
https://cn.vjudge.net/problem/HYSBZ-2002
思路
把第i只羊链接到第i+k只羊，可构成树，按题目的意思是动态切边和连边，因此猜到使用LCT
开一个虚拟根节点rt，初始时把所有羊连接到那个节点，同时开数组sav[i]记录第i只羊目前直接链接哪只羊，切边和连边动态维护即可
除了rt设每个点的点值为1，动态维护和，那么答案就是(i, rt)的路径权值和

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#define lson ch[x][0]
#define rson ch[x][1]
using namespace std;
typedef long long ll;
const int N = 200000 + 15;
const int inf = 0x3f3f3f3f;

inline int read(){
    int x = 0;
    char ch;
    while((ch = getchar()) < '0' || ch > '9');
    while('0' <= ch && ch <= '9'){
        x = x * 10 + ch - '0';
        ch = getchar();
    }
    return x;
}

inline void writeln(int x){
    printf("%d\n", x);
}

struct LinkCutTree{
    int fa[N], ch[N][2], sum[N], val[N], lzy[N];
    int stk[N];

    inline bool nRoot(int x){
        return ch[fa[x]][0] == x || ch[fa[x]][1] == x;
    }

    void pushUp(int x){
        sum[x] = sum[lson] + sum[rson] + val[x];
    }

    void pushR(int x){
        swap(lson, rson);
        lzy[x] ^= 1;
    }

    void pushDown(int x){
        if(lzy[x]){
            if(lson)    pushR(lson);
            if(rson)    pushR(rson);
            lzy[x] = 0;
        }
    }

    void rotate(int x){
        int y = fa[x], z = fa[y];
        int p = (ch[y][1] == x), w = ch[x][p^1];
        if(nRoot(y))    ch[z][ch[z][1] == y] = x;
        ch[x][p^1] = y, ch[y][p] = w;
        if(w)   fa[w] = y;
        fa[y] = x, fa[x] = z;
        pushUp(y);
    }

    void splay(int x){
        int pstk = 0, y = x;
        for(y = x; nRoot(y); y = fa[y]){
            stk[++pstk] = y;
        }
        stk[++pstk] = y;
        while(pstk)     pushDown(stk[pstk--]);

        while(nRoot(x)){
            int y = fa[x], z = fa[y];
            if(nRoot(y))     rotate((ch[y][0] == x) ^ (ch[z][0] == y) ? x : y);
            rotate(x);
        }
        pushUp(x);
    }

    void access(int x){
        for(int y = 0; x; y = x, x = fa[x]){
            splay(x);
            rson = y;
            pushUp(x);
        }
    }

    void makeRoot(int x){
        access(x);
        splay(x);
        pushR(x);
    }

    int findRoot(int x){
        access(x);
        splay(x);
        while(lson){
            pushDown(x);
            x = lson;
        }
        return x;
    }

    void split(int x, int y){
        makeRoot(x);
        access(y);
        splay(y);
    }

    void link(int x, int y){
        makeRoot(x);
        if(findRoot(y) != x)    fa[x] = y;
    }

    void cut(int x, int y){
        makeRoot(x);
        if(findRoot(y) == x && fa[x] == y && !rson){
            fa[x] = ch[y][0] = 0;
            pushUp(y);
        }
    }
};

LinkCutTree lct;
int sav[N];

int main(){
    int n = read(), rt = n + 1;
    for(int i = 1; i <= n; i++){
        lct.val[i] = 1;
        int dis = read();
        if(i + dis <= n){
            lct.cut(i, rt);
            lct.link(i, i + dis);
            sav[i] = i + dis;
        }else{
            lct.link(i, rt);
            sav[i] = rt;
        }
    }

    int m = read();
    while(m--){
        int op = read();
        if(op == 1){
            int u = read() + 1;
            lct.split(u, rt);
            writeln(lct.sum[rt]);
        }else{
            int u = read() + 1, dis = read();
            lct.cut(sav[u], u);
            if(u + dis <= n){
                lct.link(u, u + dis);
                sav[u] = u + dis;
            }else{
                lct.link(u, rt);
                sav[u] = rt;
            }
        }
    }
}