模拟退火
前言
早上大雾课在看数建,花了半节课看完了模拟退火(不要指责窝为什么上课划水,你什么时候看见窝认真听课了(此处为期末翻车埋下了伏笔))
模拟退火总的来说是玄学算法hhhh,用来求一些难以用精确算法求解的问题(NP问题),比如TSP之类的
本篇只有一道题,方便日后搞成模板而已,毕竟近似算法ACM不常用
洛谷P1337 - [JSOI2004]平衡点 _ 吊打XXX
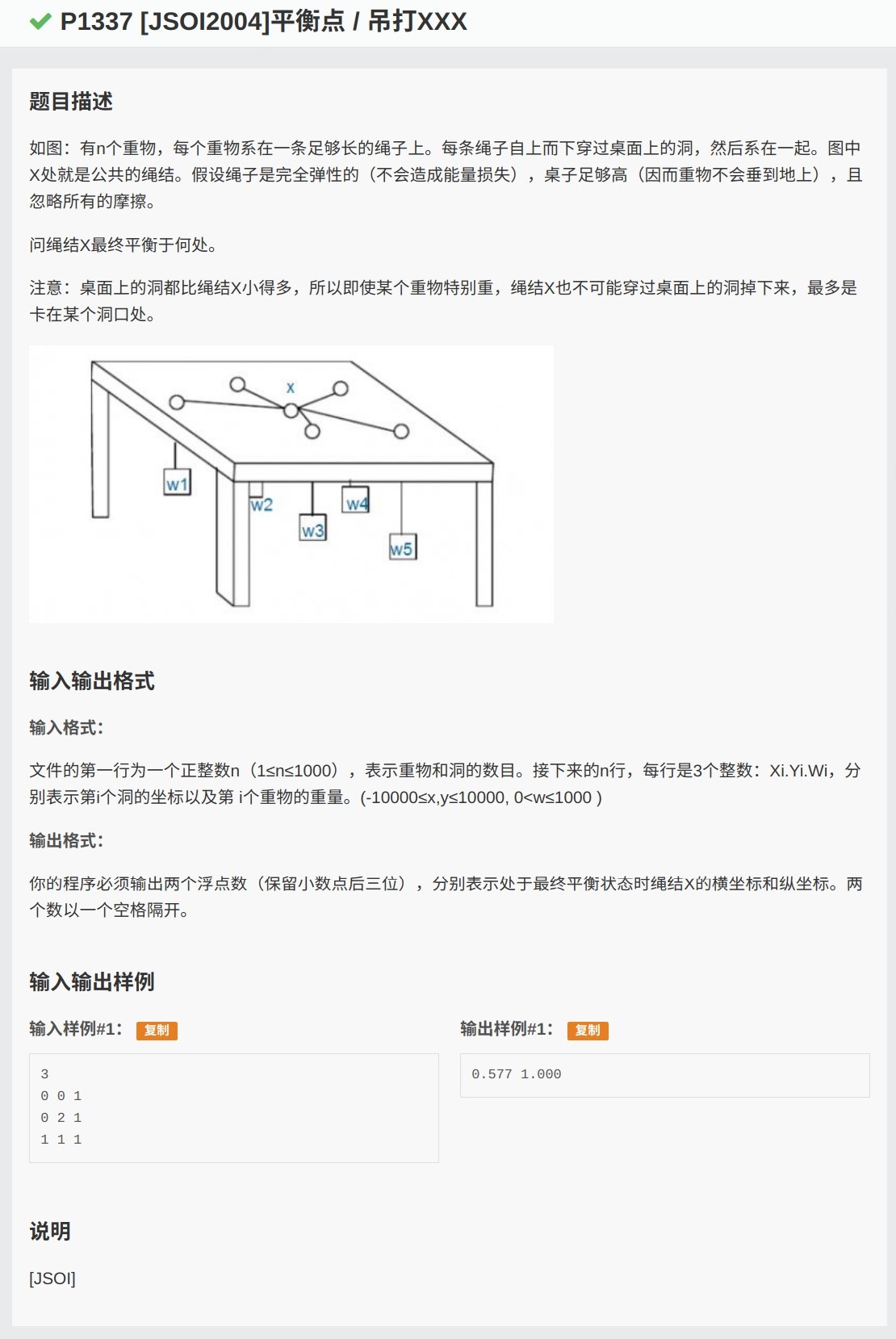
链接
https://www.luogu.org/problemnew/show/P1337
#include <cstdio>
#include <cstring>
#include <cmath>
#include <ctime>
#include <algorithm>
using namespace std;
const int N = 1000 + 15;
struct Point{
double x, y;
int w;
};
Point pt[N];
const int dx[] = {1, 0, -1, 0};
const int dy[] = {0, 1, 0, -1};
inline double sqr(double x){
return x * x;
}
inline double getDis(const Point& a, const Point& b){
return sqrt(sqr(a.x - b.x) + sqr(a.y - b.y));
}
double getSum(Point p, int n){
double ret = 0;
for(int i = 1; i <= n; i++){
ret += (getDis(p, pt[i]) * pt[i].w);
}
return ret;
}
void solve(Point& ansu, int n){
const double delta = 0.998;
const double eps = 1e-17;
double tp = 10000;
double ans = getSum(ansu, n);
Point u = ansu;
while(tp > eps){
Point v = Point{u.x + (rand()*2-RAND_MAX)*tp, u.y + (rand()*2-RAND_MAX)*tp, 1};
double tmp = getSum(v, n);
if(tmp < ans){
ansu = v;
u = v;
ans = tmp;
}else if(exp(-(tmp - ans)/tp) * RAND_MAX > rand()){
u = v;
}
tp *= delta;
}
}
int main(){
srand(time(0));
int n;
while(~scanf("%d", &n)){
for(int i = 1; i <= n; i++){
scanf("%lf%lf%d", &pt[i].x, &pt[i].y, &pt[i].w);
}
Point ansu = pt[1];
solve(ansu, n);
solve(ansu, n);
solve(ansu, n);
printf("%.3f %.3f\n", ansu.x, ansu.y);
}
return 0;
}


